Descartes e a Matemática

    Descartes é um dos grandes matemáticos de todos os tempos. Ele foi um dos fundadores da geometria analítica: a geometria passou a beneficiar da linguagem da análise, mais fácil de manejar e, por outro lado, a análise ganhou com o suporte intuitivo fornecido pela geometria.

    Foi no decorrer do ano de 1637 que Descartes concluiu o Discurso do Método acompanhado de três anexos, o último dos quais A Geometria. Escrita com a intenção de ilustrar matematicamente as considerações filosóficas gerais do Discurso do Método relativamente ao método científico, A Geometria é a única obra matemática publicada pelo filósofo e matemático, ocupando uma centena de páginas.

Página de La Geometrie

    De entre os vários domínios matemáticos em que Descartes trabalhou, salientamos os seguintes:

• Geometria analítica

• Álgebra geométrica

• Classificação das curvas

• Identificação de cónicas

• Normais e tangentes

    Foi Descartes quem, imaginando o sistema de coordenadas de um ponto,  construiu as bases da Geometria Analítica. Para dar a sua justa relevância e homenagear esse facto,  denominam-se ainda hoje de cartesianos os referenciais em que se representam graficamente as funções.

    Recordemos brevemente como se constroem esses gráficos:

Correspondência entre o plano e IR²

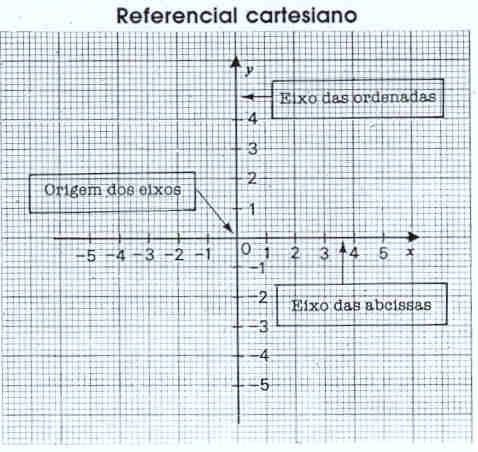
·         Traçamos duas rectas orientadas perpendiculares que se intersectam num ponto 0, origem dos eixos.

·         Escolhemos uma unidade e representamos os números inteiros nas duas rectas.

·         No eixo horizontal, os números positivos são representados à direita do ponto 0.

·         No eixo vertical os números positivos são representados acima do ponto 0.

·         Ao eixo horizontal chamamos eixo das abcissas ou eixo dos xx.

·         Ao eixo vertical chamamos eixo das ordenadas ou eixo dos yy.

       Designamos este conjunto de eixos por referencial cartesiano.

    Para determinar o ponto correspondente a um par ordenado, devemos ter em conta que:

1.      O 1º elemento é a abcissa do ponto - 1ª coordenada.

2.      O 2º elemento é a ordenada do ponto - 2ª coordenada.

3.      Os dois elementos constituem as coordenadas do ponto.

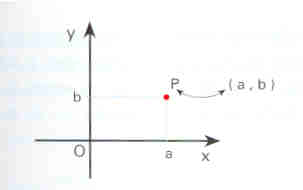
    A um par ordenado de números reais (o primeiro no eixo dos xx e o segundo no dos yy) corresponde um ponto do plano que se situa na intersecção da recta paralela ao eixo dos yy que passa no ponto do eixo dos xx de abcissa a, com a recta paralela ao eixo dos xx que passa no ponto do eixo dos yy de ordenada b.

    Assim, se P for o conjunto dos pontos do plano e IR² o conjunto de todos os pares ordenados de números reais, podemos estabelecer uma correspondência biunívoca entre P e IR²: a cada ponto corresponde um par e reciprocamente.

    O plano fica dividido em quatro partes - os quadrantes.

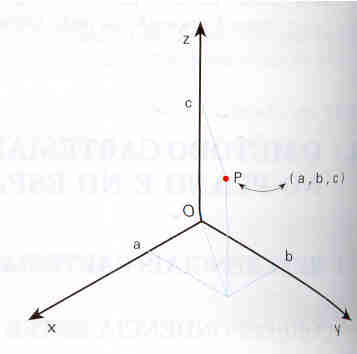
Correspondência entre o espaço e IR³

    Consideram-se três eixos, perpendiculares dois a dois, com a mesma origem em O: o eixo dos xx ou das abcissas, o eixo dos yy ou das ordenadas e o eixo dos zz ou das cotas.

    A um terno de números reais (em que o primeiro é a abcissa, o segundo a ordenada e o terceiro a cota) corresponde um ponto do espaço, obtido através de paralelas aos eixos.

    Os eixos, dois a dois, definem, assim, planos - chamados planos coordenados, ou seja, xOy, yOz e xOz.

    Deste modo, se E for o conjunto de todos os pontos do plano e IR³ o conjunto de todos os ternos ordenados de números reais, podemos estabelecer uma correspondência biunívoca entre E e IR³: a cada ponto do espaço corresponde um terno de números reais e reciprocamente.

    O espaço fica dividido em oito porções - os octantes.

    Todas as leis da geometria euclidiana permanecem verdadeiras nesta nova geometria. Por exemplo, na geometria euclideana uma recta é descrita por dois pontos e, na geometria cartesiana, uma vez que um ponto é descrito por um par de números, então uma recta pode ser descrita por dois pares.

    Um exemplo do trabalho de Descartes utilizando o conceito de coordenadas é o da demonstração de que as diagonais de um rectângulo têm comprimentos iguais.

    Vejamos agora alguns exemplos simples no âmbito do  seu trabalho em Algebra Geométrica.

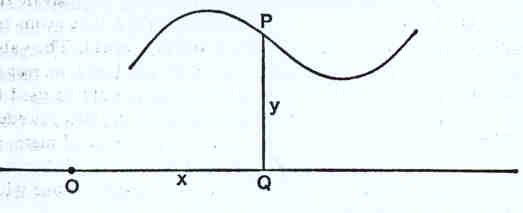
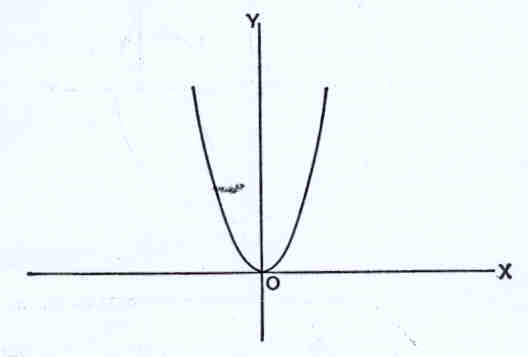
  1. Consideremos uma curva como mostra a figura:

e seja P um ponto da curva. Podemos, assim, estudar a curva se analisarmos a posição do ponto P que se desloca para cima ou para baixo quando a linha vertical se move para a direita ou esquerda. A posição é, pois, a distância x a um ponto fixo O. A linha vertical PQ dá-nos a distância, y, a que o ponto P se encontra acima da linha OQ. Deste modo, para cada posição de P teremos um valor de x e de y. O que caracteriza cada curva é, pois, a relação entre x e y.

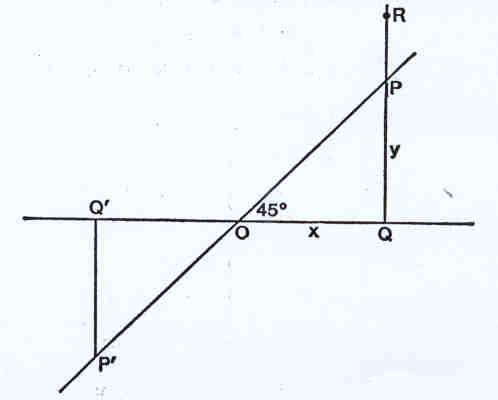
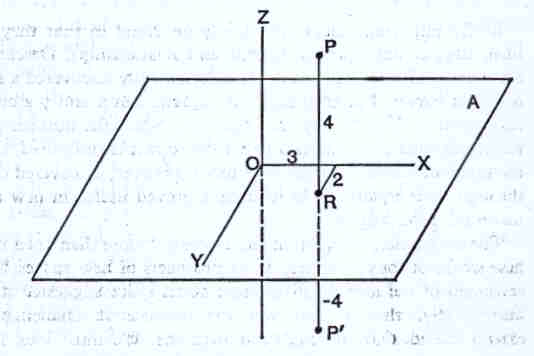
    2. Consideremos uma linha recta que passe pelo ponto O e que faça um ângulo de 45º com a linha horizontal, como mostra a figura:

    Se deslocarmos a linha PQ, haverá uma posição P tal que a distância y será igual a x. OQP forma, assim, um triângulo isósceles, ou seja, OQ é igual a OP. Temos que y=x caracteriza qualquer ponto da linha recta, isto é, para um ponto fazer parte da linha recta ele terá de satisfazer a equação y=x. Ao ponto R, por exemplo, corresponde um valor y diferente do de x, ou seja, R não pertence à linha recta.

   Se considerarmos, como já vimos, um sistema de eixos perpendiculares com intersecção O, temos que qualquer ponto de uma curva fica definido pelo valor de x (abcissa de P) e pelo valor de y (ordenada de P).

    3. Vejamos ainda como a equação da circunferência que conhecemos, surgiu naturalmente para Descartes.

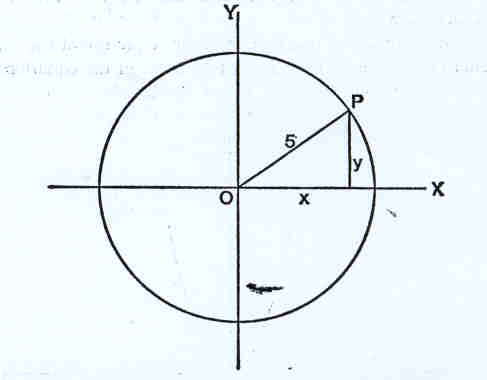
    Consideremos a seguinte figura:

onde o raio da circunferência é 5. O Teorema de Pitágoras diz-nos, pois, que x²+y²=25, pois x e y são os catetos de um triângulo rectângulo de hipotenusa 5.

    Assim, cada ponto P da circunferência de coordenadas (x,y) satisfaz esta equação. Qualquer ponto que não pertença à circunferência, não satisfaz aquela equação.

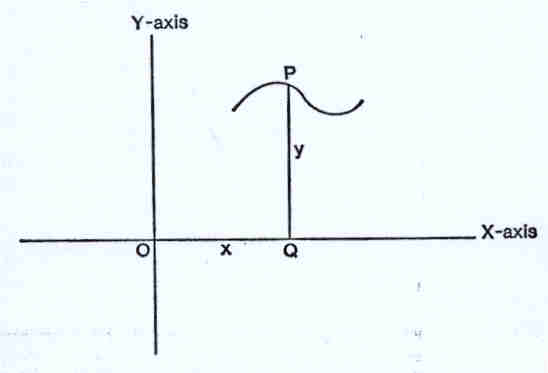
    A Geometria de Descartes também permite representar uma curva quando nos é dada uma equação.

    4. Consideremos agora a equação y=x². Que tipo de curva lhe estará associada?
    Sabe-se que à direita de O, o valor da abcissa de P, isto é, de x, é positivo. A equação dá-nos um valor de y igual a x². Temos então que a ordenada também será positiva, ou seja, ficará acima do eixo dos xx.
    Nota-se ainda que para valores pequenos de x se têm valores pequenos de y. Contudo, para valores maiores de x, o valor de y aumenta consideravelmente.
    Assim, é fácil imaginar o aspecto que tomará a curva para valores de x à direita de O.

    Por outro lado, quando PQ se move para a esquerda de O, o valor da abcissa de P é negativo. Porém, o valor de y é x² que é positivo.
    Deste modo, para x e -x obtém-se o mesmo valor de y. A curva tomará então o mesmo comportamento que a anterior mas no sentido contrário, ou seja, para valores muito pequenos à esquerda de O, y tomará valores muito grandes. Aproximando-nos de O, verificamos que y tomará valores pequenos. A curva terá então a forma:

onde se verifica haver uma simetria em relação ao eixo dos yy.

    Esta associação entre equação e curvas, possibilitou várias aplicações em diversos campos, em especial do domínio científico. As curvas foram, mais tarde, utilizadas em telescópios, microscópios, máquinas de raio-X,...
    Além disso, proporcionou a expansão desta ideia a um espaço tridimensional.
    Descartes verificou que podia descrever a posição de um ponto por um terno de números, como acima referimos.

    Tal como no plano, Descartes também verificou ser possível relacionar equações algébricas e figuras geométricas no espaço.

    Vejamos alguns exemplos.

• A esfera

    A esfera é um conjunto de pontos no espaço que estão situados à mesma distância de um ponto - o centro da esfera.

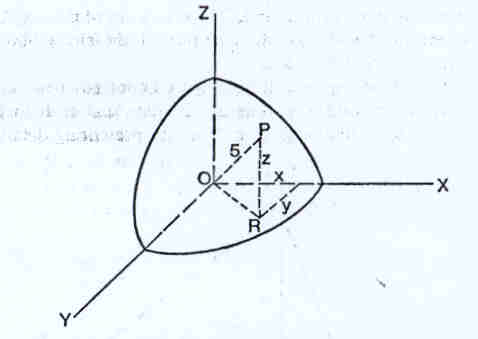
    Consideremos o seguinte exemplo como mostra a figura, cujos pontos distam 5 unidades do centro da esfera. Seja ainda o centro da esfera coincidente com a origem do referencial a três dimensões. Um ponto P na esfera tem coordenadas (x,y,z). Verifica-se que x e y são os catetos de um triângulo rectângulo com hipotenusa OR. Pelo teorema de Pitágoras, tem-se:
x²+y²=OR².          (1)
    OR e z são, por sua vez, os catetos do triângulo rectângulo ORP, cuja hipotenusa é OP, ou seja, 5 unidades. Da mesma forma se vê que
OR²+z²=25.
    Substituindo OR² pelo valor de (1), temos que x²+y²+z²=25.
    Esta é a equação da esfera. Qualquer ponto que esteja na esfera satisfaz esta equação.

    Notemos as semelhanças desta equação com a da circunferência.

• O parabolóide

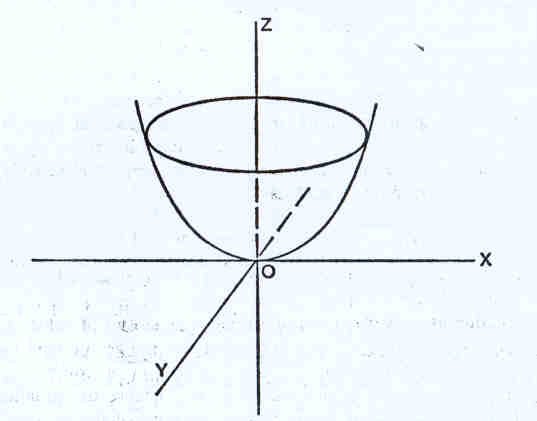
    Tal como para a esfera, chegamos à seguinte equação do parabolóide x²+y²=z, que tem muitas semelhanças também com a equação da parábola y=x².

    Existe, assim, uma ligação entre as equações das figuras no plano e no espaço.

    Estavam, pois, abertos os caminhos para se explorar uma geometria no espaço. O mundo físico podia ser visto a quatro dimensões. Qualquer acontecimento tem lugar num certo espaço e tempo. A posição no espaço poderia ser dada por um terno de números x, y e z, e o tempo seria a quarta coordenada t.
    Esta nova perspectiva permitia, por exemplo, descrever a posição dos planetas que a cada momento ocupam uma determinada posição no espaço.