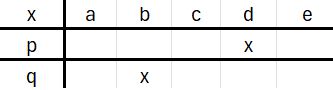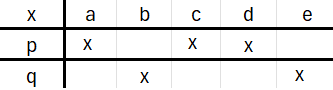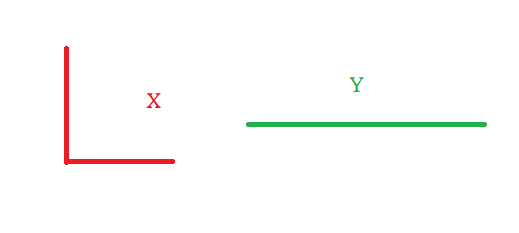Metric spaces and topology

by Cristian Barbarosie

This is a textbook accompanying the course "Topologia" at FCUL.

Remark (conceptual minimalism)

The presentation tries to use only the essential and necessary concepts and notations. For instance, it avoids references to nets (or filters), adherent points, accumulation points, total boundedness, separable space, Lindelöf space, quasi-compact space, paracompact space.

Items in orange are considered advanced topics.

Preliminary concepts

1. Set theory, mathematical logic

Remark 1.1 (concept of set)

We do not define the notion of set. We can describe intuitively a set as any collection of elements.

Remark 1.2 (propositions, boolean operations)

We assume that the reader is familiar with the concepts of proposition, value of truth and boolean operations and, or and not. One can use the notations P∧Q for P and Q, P∨Q for P or Q and P for not P.

Remark 1.3 (logical or)

It should be noted that, in everyday language, the meaning of the word "or" is sometimes different from the meaning of the operator or in mathematical logic. This can be explained through the following joke.
A man and a woman are talking casually and the man asks "are you married or single ?" The woman, who is a mathematician specialized in logic, after thinking for a while, answers "yes".
Explanation : in everyday language, the word "or" is often mutually exclusive and implies a choice between two possibilities. In mathematical logic, or means simply that at least one of the propositions involved is true.
In programming, there is a different operator called exclusive or whose meaning is somewhat closer to the everyday language.

Properties 1.4 (commutativity, distributivity)

The boolean operations verify the following properties which are easy to check by giving propositions P, Q and R all possible truth value combinations.
a) P and Q ≡ Q and P (the conjunction is commutative)
b) P or Q ≡ Q or P (the disjunction is commutative)
c) (P and Q) and R ≡ P and (Q and R) (the conjunction is associative)
d) (P or Q) or R ≡ P or (Q or R) (the disjunction is associative)
e) (P or Q) and R ≡ (P and R) or (Q and R) (the disjunction is distributive with respect to the conjunction)
f) (P and Q) or R ≡ (P or R) and (Q or R) (the conjunction is distributive with respect to the disjunction)

Note how operators and and or play symmetric roles with regard to distributivity. This is very different from arithmetic operators of addition and multiplication : multiplication is distributive with respect to addition but not the other way around.

g) not (not P) ≡ P
h) not (P and Q) ≡ (not P) or (not Q)
i) not (P or Q) ≡ (not P) and (not Q)

Definition 1.5 (predicate)

A proposition p which depends on a parameter x is called a predicate and is denoted by p(x).

Remark 1.6 (correspondence between sets and predicates)

To each set A we can associate the predicate x ∊ A. Conversely, to each predicate we can associate the set of elements where the predicate is true.

Definition 1.7 (intersection, union)

Let A and B be two arbitrary sets. We call intersection of A and B to the set of all elements which belong simultaneously to A and to B; this set is denoted by A∩B. We call union of A and B to the set of all elements which belong to at least one of A and to B; this set is denoted by A∪B.

Remark 1.8 (link between intersection and and, between union and or)

Recall the association between sets and predicates, remark 1.6. This association gives a strong link between the intersection of sets and the logical operator and : x ∊ A∩B ⇔ (x ∊ A) and (x ∊ B). There is also a strong link between the union of sets and the logical operator or : x ∊ A∪B ⇔ (x ∊ A) or (x ∊ B).

Properties 1.9 (commutativity, distributivity)

The link shown in remark 1.8 means that the properties of logical operators (remark 1.4) imply corresponding properties of intersection and union of sets :
a) A∩B = B∩A (intersection is commutative)
b) (A∩B) ∩ C = A ∩ (B∩C) (intersection is associative)
c) A∪B = B∪A (union is commutative)
d) (A∪B) ∪ C = A ∪ (B∪C) (union is associative)
e) (A∪B) ∩ C = (A∩C) ∪ (B∩C) (intersection is distributive with respect to union)
f) (A∩B) ∪ C = (A∪C) ∩ (B∪C) (union is distributive with respect to intersection)

Definition 1.10 (complementary set)

If we assume all possible elements belong to some large, surrounding set 𝒰 (the universe), we can define the complementary of a given set A as the set ∁A of all elements which do not belong to A.
Some authors use the notation A for the complementary set.
In the spirit of remark 1.8, there is a strong link with the logical operator not. Thus, properties g), h) and i) in remark 1.4 imply :
a) the complementary of ∁A is A
b) ∁(A∩B) = ∁A ∪ ∁B
c) ∁(A∪B) = ∁A ∩ ∁B

Definition 1.11 (existential and universal quantifiers)

The existential quantifier ∃ and the universal quantifier ∀ transform a predicate into a regular proposition. If p(x) is a predicate (a proposition depending on a parameter x ∈ A) then ∃ x ∈ A, p(x) is a new proposition meaning "there exists an x in A for which p(x) is true". It can also be formulated as "there exists at least one x in A for which p(x) is true". On the other hand, ∀ x ∈ A, p(x) is a different proposition meaning "for any x ∈ A, p(x) is true".
Note that the expressions ∃ x ∈ A, p(x) and ∀ x ∈ A, p(x) are not predicates, their value of truth does not depend on a parameter. In particular ∃ x ∈ A, p(x) and ∃ y ∈ A, p(y) are two different ways of expressing the very same proposition (the parameter name, x or y, is meaningless outside that logical expression). Similarly, ∀ x ∈ A, p(x) and ∀ y ∈ A, p(y) are exactly the same proposition.

Property 1.12 (negation of quantifiers)

Let p(x) be a predicate on a set A. Then
not (∀ x ∈ A, p(x)) ≡ ∃ x ∈ A, not p(x)
not (∃ x ∈ A, p(x)) ≡ ∀ x ∈ A, not p(x)

The importance of understanding these two properties cannot be overstated.
The first of these properties can be intuitively described as follows. Suppose somebody says "all birds fly". If I want to explain to this person that their statement is false, I don't say "no bird can fly"; if I say this I will be equally wrong. I must say "although most birds do fly, there are birds which do not, like the penguin or the ostrich". Formally : the negation of "∀ x ∈ {birds}, x flies" is not "∀ x ∈ {birds}, x does not fly" but "∃ x ∈ {birds}, x does not fly".

Remark 1.13 (quantifiers applied to the void set)

No matter which predicate p we choose, the proposition ∃ x ∈ ∅, p(x) is always false.
No matter which predicate p we choose, the proposition ∀ x ∈ ∅, p(x) is always true.

While the first of the statements above should be self-evident, the second one is much less obvious and actually many people have some degree of trouble accepting it or fully understanding it. Here is a way to think about it. Let us apply the first statement to the predicate not p; so ∃ x ∈ ∅, not p(x) is always false. Its negation is ∀ x ∈ ∅, p(x) (see property 1.12); it must be always true.

Questions 1.14

Let p and q be two predicates on a set A. Are the statements below equivalent ?
a) (∃ x ∈ A, p(x)) and (∃ x ∈ A, q(x))  versus  ∃ x ∈ A, (p(x) and q(x))
b) (∀ x ∈ A, p(x)) and (∀ x ∈ A, q(x))  versus  ∀ x ∈ A, (p(x) and q(x))
c) (∃ x ∈ A, p(x)) or (∃ x ∈ A, q(x))  versus  ∃ x ∈ A, (p(x) or q(x))
d) (∀ x ∈ A, p(x)) or (∀ x ∈ A, q(x))  versus  ∀ x ∈ A, (p(x) or q(x))

Answers

In a), the assertion on the left is true if two different x₁ and x₂ exist such that p(x₁) and p(x₂) are true. The assertion on the right needs x₁ and x₂ to be the same. Thus, they are not equivalent. The assertion on the right implies the on on the left. For instance, if p and q are the predicates shown below, the assertion on the left holds true but not the one on the right.

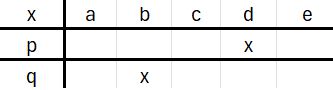
In b) and c), the two assertions are equivalent.
In d), the assertion on the left implies the assertion on the right but not the other way around. For instance, if p and q are the predicates shown below, the assertion on the right holds true but not the one on the left.

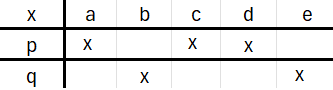
Definition 1.15 (cartesian product of two sets)

For two given sets A and B, their cartesian product A × B is the set of all pairs (a,b), with a ∈ A and b ∈ B.

Definition 1.16 (predicate depending on several parameters)

There are predicates depending on more than one parameter. For instance, a predicate p(x,y) depending on two parameters, x ∈ A and y ∈ B, is simply a predicate on A × B.
Such a predicate may be called bi-variate. Since a predicate on a set A corresponds to a subset of A (see remark 1.6), a bi-variate predicate can be viewed as a relation (see definition 2.1).

Remark 1.17 (quantifiers applied to predicates of more than one argument)

One can apply quantifiers to predicates depending on more than one parameter. For instance, if p(x,y) is a predicate depending on two parameters x ∈ A and y ∈ B, then ∀ x ∈ A, p(x,y) is a new predicate depending on only one parameter y ∈ B.
Thus, it is possible to write entire chains of quantifiers. For instance, ∀ x ∈ A, ∀ y ∈ B, p(x,y) is a proposition (does not depend on any parameter). Of course, ∀ x ∈ A, ∃ y ∈ B, p(x,y) is quite a different proposition, and so are ∃ x ∈ A, ∀ y ∈ B, p(x,y) and ∃ x ∈ A, ∃ y ∈ B, p(x,y).

Remark 1.18 (order of quantifiers)

Let p be a predicate depending on (at least) two parameters. We can switch the order of two existential quantifiers without changing the meaning of the resulting proposition. That is, ∃ x ∈ A, ∃ y ∈ B, p(x,y) is exactly the same proposition as ∃ y ∈ B, ∃ x ∈ A, p(x,y). Both mean there is a pair (x,y) in A × B such that p(x,y) is true.
Similarly, ∀ x ∈ A, ∀ y ∈ B, p(x,y) yelds exactly the same as ∀ y ∈ B, ∀ x ∈ A, p(x,y). Both mean that for any pair (x,y) in A × B, p(x,y) is true. That is, p is true on A × B.
However, ∃ x ∈ A, ∀ y ∈ B, p(x,y) is very different from ∀ y ∈ B, ∃ x ∈ A, p(x,y) ! The first statement means there exists a particular x ∈ A, which we may call x^⋆, such that p(x^⋆,y) is true for all y ∈ B. That is, p is true on {x^⋆} × B. The second statement means that, for each y ∈ B there is an x ∈ A such that p(x,y) is true; this x may depend (and often does) on the chosen y and thus may be denoted by x(y). The importance of understanding the difference between these two situations cannot be overstated.

Challenges 1.19 (order of quantifiers)

Consider A = {a,b,c,d,e} and B = {1,2,3,4}. Consider the three predicates represented below, where a cross means true and an empty field means false.

For each of these predicates, determine the value of truth of the following propositions.
a) ∃ x ∈ A, ∃ y ∈ B, p(x,y)
b) ∀ x ∈ A, ∃ y ∈ B, p(x,y)
c) ∃ y ∈ B, ∀ x ∈ A, p(x,y)
d) ∀ y ∈ B, ∃ x ∈ A, p(x,y)
e) ∃ x ∈ A, ∀ y ∈ B, p(x,y)
f) ∀ x ∈ A, ∀ y ∈ B, p(x,y)

Questions 1.20 (order of quantifiers, x ≤ y)

Are the following propositions true or false ?
a) ∃ x ∈ ℕ, ∃ y ∈ ℕ, x ≤ y
b) ∀ x ∈ ℕ, ∃ y ∈ ℕ, x ≤ y
c) ∃ y ∈ ℕ, ∀ x ∈ ℕ, x ≤ y
d) ∀ y ∈ ℕ, ∃ x ∈ ℕ, x ≤ y
e) ∃ x ∈ ℕ, ∀ y ∈ ℕ, x ≤ y
f) ∀ x ∈ ℕ, ∀ y ∈ ℕ, x ≤ y

Answers

a) is true
b) is true
c) is false (there is no y greater than any natural number)
d) is true (it suffices to choose x=y)
e) is true (it suffices to choose as x the lowest natural number)
f) is false

Questions 1.21 (order of quantifiers, x ≤ y)

Are the following propositions true or false ?
a) ∃ x ∈ ℝ, ∃ y ∈ ℝ, x ≤ y
b) ∀ x ∈ ℝ, ∃ y ∈ ℝ, x ≤ y
c) ∃ y ∈ ℝ, ∀ x ∈ ℝ, x ≤ y
d) ∀ y ∈ ℝ, ∃ x ∈ ℝ, x ≤ y
e) ∃ x ∈ ℝ, ∀ y ∈ ℝ, x ≤ y
f) ∀ x ∈ ℝ, ∀ y ∈ ℝ, x ≤ y

Answers

a) is true
b) is true
c) is false (there is no y greater than any real number)
d) is true (it suffices to choose x=y)
e) is false (there is no x smaller than any real number)
f) is false

Questions 1.22 (order of quantifiers, x² ≤ y)

Are the following propositions true or false ?
a) ∃ x ∈ ℝ, ∃ y ∈ ℝ, x² ≤ y
b) ∀ x ∈ ℝ, ∃ y ∈ ℝ, x² ≤ y
c) ∃ y ∈ ℝ, ∀ x ∈ ℝ, x² ≤ y
d) ∀ y ∈ ℝ, ∃ x ∈ ℝ, x² ≤ y
e) ∃ x ∈ ℝ, ∀ y ∈ ℝ, x² ≤ y
f) ∀ x ∈ ℝ, ∀ y ∈ ℝ, x² ≤ y

Answers

a) is true
b) is true
c) is false (there is no y greater than any square of a real number)
d) is false (it suffices to choose y negative)
e) is false (one can always choose a y smaller than a given value)
f) is false

Questions 1.23 (order of quantifiers, x ≤ y²)

Are the following propositions true or false ?
a) ∃ x ∈ ℝ, ∃ y ∈ ℝ, x ≤ y²
b) ∀ x ∈ ℝ, ∃ y ∈ ℝ, x ≤ y²
c) ∃ y ∈ ℝ, ∀ x ∈ ℝ, x ≤ y²
d) ∀ y ∈ ℝ, ∃ x ∈ ℝ, x ≤ y²
e) ∃ x ∈ ℝ, ∀ y ∈ ℝ, x ≤ y²
f) ∀ x ∈ ℝ, ∀ y ∈ ℝ, x ≤ y²

Answers

a) is true
b) is true
c) is false (there is no number greater than all real numbers)
d) is true (it suffices to choose x=0 or negative)
e) is true (it suffices to choose x=0 or negative)
f) is false

Questions 1.24 (order of quantifiers, n𝜀 > 1)

Are the following propositions true or false ?
a) ∀ 𝜀 > 0, ∃ n ∈ ℕ, n𝜀 > 1
b) ∃ n ∈ ℕ, ∀ 𝜀 > 0, n𝜀 > 1

Answers

a) is true, it suffices to choose some n larger than 1/𝜀
b) is false, it suffices to choose an 𝜀 smaller than 1/n

Remark 1.25 (two players)

In questions 1.20, 1.21, 1.22, 1.23, 1.24, 1.26, one can imagine two players. Focusing on 1.24, ...

Questions 1.26 (order of quantifiers, n𝜀 > 1)

Are the following propositions true or false ?
a) ∀ 𝜀 > 0, ∃ N ∈ ℕ, ∀ n ≥ N, n𝜀 > 1
b) ∃ N ∈ ℕ, ∀ 𝜀 > 0, ∀ n ≥ N, n𝜀 > 1
c) ∃ N ∈ ℕ, ∀ n ≥ N, ∀ 𝜀 > 0, n𝜀 > 1

Answers

a) is true (it suffices to choose N greater than 1/𝜀),
b) is false (no matter how large N is, we can always choose an 𝜀 small enough to violate the desired inequality),
c) is identical to b) (switching the order of two universal quantifiers does not change the meaning of the sentence)

Remark 1.27 (use of functions)

In the sequel, we will dwell on the concept of finite (versus infinite) set. For defining this concept we will need to use the notion of bijective function, see definition 3.2.

Question 1.28 (bijections between sets)

Is there any bijection between the sets {a,b,c,d,e} and {1,2,3,4} ?

Remark 1.29 (about natural numbers)

The negative answer to question 1.28 is a hint at how natural numbers show up as a cognitive necessity. We can say that the number 5 is a common characteristic of all sets which are in bijection (in a one-to-one correspondence) with the set of the fingers of one of our hands. The set {a,b,c,d,e} is one of these sets.

Question 1.30 (bijection between a set and a subset)

Is there any bijection between the set {a,b,c,d,e} and any of its subsets ?

Answer

Yes, if we take the subset to be {a,b,c,d,e} itself.

Question 1.31 (bijection between a set and a proper subset)

Is there any bijection between the set {1,2,3,...,1000000} and any of its proper subsets ?
A subset A of a set X is said to be proper if A ≠ X.

Answer

No.

Question 1.32 (bijection between ℕ and a proper subset)

Is there any bijection between the set ℕ of natural numbers and the set of natural numbers starting at 10 {10,11,12,13,...} ?

Answer

Yes, for instance n↦ n+10 (assuming ℕ starts at 0).

Question 1.33 (bijection between ℕ and ℤ)

Is there any bijection between the set of natural numbers ℕ and the set of integer numbers ℤ ?

Answer

Definition 1.34 (finite sets)

The positive answer to questions 1.32 and 1.33 suggests that there is an important difference between sets like ℕ or ℤ and other sets like {a,b,c,d,e} or {1,2,3,...,1000000}. We say that a set X is infinite if there is a bijection between X and some proper subset of it. Naturally, we say that a set X is finite if it is not infinite.

Property 1.35 (bijection between ℕ and ℕ × ℕ)

There is a bijection between ℕ and ℕ × ℕ. Find it. There are several possible answers.

Answer

One possibility is the Cantor pairing function.
bijection between N and NxN

Questions 1.36 (are there bijections ?)

a) Is there a bijection between the set of natural numbers ℕ and the set of rational numbers ℚ ?
b) Is there a bijection between the set of natural numbers ℕ and the interval [0,1[ ?
c) Is there a bijection between the intervals [0,1[ and ]0,1[ ?
d) Is there a bijection between the intervals ]0,1[ and ]-1,1[ ?
e) Is there a bijection between the interval [0,1[ and the semi-line [0,+∞[ ?
f) Is there a bijection between the interval ]-1,1[ and the set of real numbers ℝ ?
g) Is there a bijection between the set of natural numbers ℕ and the set of real numbers ℝ ?
h) Is there a bijection between the interval [0,1[ and the square [0,1[² ⊂ ℝ² ?

Answers

a )yes; one can make use of the bijection mentioned in property 1.35
b) no, see e.g. this paper
c) yes
d) yes,  f(x) = 2x-1
e) yes,  f(x) = tan (pi x /2) or f(x) = x/(1-x)
f) yes,  f(x) = tan (pi x /2)
g) no; this can be proven based on questions 1.36.b, 1.36.c, 1.36.d and 1.36.f
h) yes, see e.g. this page

Definition 1.37 (countable set)

We say that a set X is countable if there is a one-to-one correspondence between X and ℕ. A countable set is infinite. We say that a set X is uncountable if it is infinite and not countable.
Thus, sets can be classified in three categories : finite sets, countable sets and uncountable sets.

Remark 1.38 (countable and uncountable sets)

Question 1.36.a can be reformulated as : ℚ is countable. Question 1.36.g can be reformulated as : ℝ is uncountable.

Remark 1.39 (terminology)

The adjective "countable" is somewhat misleading. The elements of a set like ℕ or ℚ cannot be "counted" since these sets are infinite. Rather, they can be organized as a sequence; thus, an adjective like "sequentiable" could have been used. However, the word "countable" is widely used in the literature.

Remark 1.40

We will use the adjective "countable" in a flexible way. Sometimes, "countable" will imply infinite. On some occasions (e.g. in items 13.40, 13.45), the word "countable" should be understood as "finite or countable". In item 17.8, it does not matter which meaning of "countable" we assume.

Definition 1.41 (set of subsets)

In items 1.42 - 1.47 we will focus on collections of subsets of a given set X. The set of all subsets of X (including the empty set ∅ and the set X itself) will be denoted by 𝒫(X). So, we will focus on subsets of 𝒫(X).

Definition 1.42 (covering)

A collection 𝒜 of non-empty subsets of X is called a covering of X if the union of all sets in 𝒜 equals X, that is, ⋃𝒜 = X.

Remark 1.43 (covering of a subset)

Sometimes we will consider a subset C of X and will call covering of C to any collection 𝒜 of non-empty subsets of X such that the union of all sets in 𝒜 contains C, that is, ⋃𝒜 ⊃ C.
In this case, the collection { A∩C : A∈𝒜 } will be a covering of C in the sense of definition 1.42.

Examples 1.44 (coverings)

The following are examples of coverings of the set of natural numbers ℕ.
a) { ℕ }
b) { {1,2,3}, {i ∈ ℕ : i ≥4} }
c) { the set of even numbers, the set of numbers divisible by 3, the set of odd numbers }
d) { {n} : n ∈ ℕ }
e) { {1,2,3,...,n} : n ∈ ℕ }
Note that coverings a), b) and c) are finite while d) and e) are infinite.

Remark 1.45 (items 1.46 and 1.47 can be read later)

Items 1.46 and 1.47 below are related to the notion of compact topologic space. Their reading can be postponed.

Definition 1.46 (subcovering)

Let 𝒜 be a covering of X. Consider 𝒜^⋆ a subfamily of 𝒜 (𝒜^⋆ is obtained from 𝒜 by eliminating some of the sets). If 𝒜^⋆ still covers X (that is, ⋃𝒜^⋆ = X), we say that 𝒜^⋆ is a subcovering of 𝒜.

Questions 1.47 (coverings)

a) Is the family { [n, n+1] : n ∈ ℕ } a covering of ℝ ? How many intervals can we withdraw from it and still get a covering of ℝ ?
b) Is the family { [-n, n] : n ∈ ℕ } a covering of ℝ ? How many intervals can we withdraw from it and still get a covering of ℝ ?
c) Is the family { ]-n, n[ : n ∈ ℕ } a covering of ℝ ? How many intervals can we withdraw from it and still get a covering of ℝ ?
d) Is the family { [n, n+1] : n ∈ ℕ } a covering of ℝ ? Does it have a finite subcovering ?
e) Is the family { [0, n] : n ∈ ℕ } a covering of ℝ ? Does it have a finite subcovering ?
f) Is the family { [0, n] : n ∈ ℕ } a covering of [0,+∞[ ? Does it have a finite subcovering ?
g) Is the family { [1/n,1] : n ∈ ℕ, n > 0 } a covering of [0,1] ? Does it have a finite subcovering ?
h) Is the family { ]1/n,1] : n ∈ ℕ, n > 0 } a covering of [0,1] ? Does it have a finite subcovering ?
i) Is the family { ]1/n,1] : n ∈ ℕ, n > 0 } a covering of ]0,1] ? Does it have a finite subcovering ?
j) Is the family { ]1/n,1[ : n ∈ ℕ, n > 0 } a covering of ]0,1] ? Does it have a finite subcovering ?
k) Is the family { ]1/n,1[ : n ∈ ℕ, n > 0 } a covering of ]0,1[ ? Does it have a finite subcovering ?
l) Consider the family of subsets of ]0,1[ in question 1.47.k above. Add to this family the interval ]0, 0.001[; we obtain a new covering of ]0,1[. Does it have a finite subcovering ?

Definition 1.48 (partition)

A collection 𝒜 of non-empty subsets of X will be called a partition of X if
a) the sets in 𝒜 are mutually disjoint, that is, ∀ A,B ∈ 𝒜, A ∩ B = ∅
b) the union of all sets in 𝒜 equals X, that is, ⋃𝒜 = X

In other words, a partition is a covering with mutually disjoint sets.

Question 1.49

Which of the coverings in example 1.44 are partitions ?

Question 1.50 (subpartition)

Let 𝒜 be a partition of X. If 𝒜^⋆ is obtained by withdrawing one or several sets from 𝒜, can 𝒜^⋆ still be a partition of X ?

Answer

Remark 1.51

A partition of a set defines an equivalence relation on that set, see example 4.2.j. Conversely, any equivalence relation defines a partition, see challenge 4.9.

2. Relations

Definition 2.1 (relation)

For two given sets A and B, we call relation between elements of A and elements of B to any subset R of A × B. We say that two elements a ∈ A and b ∈ B are in relation, and we write aRb, simply if the pair (a,b) belongs to R.
This corresponds to a bi-variate predicate (definition 1.15).

Examples 2.2 (four relations)

Below we show four examples of relations between the sets A = {a,b,c,d,e} and B = {1,2,3,4}.

In the lower left example, no elements are related. In the lower right example, any two elements are related.

Definition 2.3 (function)

A function  f : A → B is a relation between elements of A and elements of B having the following property. For each x ∈ A there exists a unique y ∈ B such that x and y are in relation. Symbolically, ∀ x ∈ A, ∃ !  y ∈ B,  xRy. Since, for given x, the element y exists and is unique, we write y = f(x).
We call A the domain (or domain of definition) of the function  f. We call B the codomain of the function  f.

Examples 2.4 (two functions)

Below we show two examples of functions defined on A = {a,b,c,d,e}, with values in B={1,2,3,4}.

The function on the right is constant.

Remark 2.5 (relations between a set and itself)

In the remainder of this section, we consider relations between elements of a set and elements of itself; that is, in definition 2.1 we take A = B.

Definition 2.6 (types of relations)

Let R be a relation between a set A and itself.
R is said to be reflexive if ∀ x ∈ A, xRx.
R is said to be symmetric if ∀ x,y ∈ A, xRy ⇔ yRx.
R is said to be anti-symmetric if ∀ x,y ∈ A, ( xRy and yRx ) ⇒ x=y.
R is said to be transitive if ∀ x,y,z ∈ A, ( xRy and yRz ) ⇒ xRz.

Remark 2.7 (about transitivity)

Transitivity (see definition 2.6) means that the relationship is transmitted, is passed on.
For instance, if person a and person b have the same height and person b and person c have the same height, then of course person a and person c have the same height.
Another example is "runs faster than". A rabbit runs faster than a rat, a rat runs faster than a lizard, so of course a rabbit runs faster than a lizard. On the other hand, friendship is not necessarily transitive, either in real life or on a social network. It happens frequently that a and b are friends, b and c are friends, but a and c are not.
A nice example of relation which is not transitive is the "rock paper scissors" game. It can be viewed as a playful application of a relation on a set with three elements { rock, paper, scissors }. Rock wins to scissors, scissors win to paper but there is no transitivity : rock does not win to paper.

Question 2.8

Is any of the relations in example 2.2 reflexive ? Symmetric ? Anti-symmetric ? Transitive ?

Answer

These concepts only make sense for a relation between a set and itself. Since in example 2.2 A ≠ B, the questions do not apply.

Questions 2.9

Is any of the relations shown below reflexive ? Symmetric ? Anti-symmetric ? Transitive ?

Answers

The relation in the upper left corner is symmetric.
The relation in the upper right corner is symmetric.
The relation in the lower left corner is transitive.
The relation in the lower right corner is symmetric, anti-symmetric and transitive.

Questions 2.10

Is any of the relations shown below reflexive ? Symmetric ? Anti-symmetric ? Transitive ?

Answers

The relation in the upper left corner is reflexive and anti-symmetric.
The relation in the upper right corner is anti-symmetric and transitive.
The relation in the lower left corner is reflexive, anti-symmetric and transitive.
The relation in the lower right corner is reflexive and symmetric.

Challenge 2.11

Give an example of a relation which is simultaneously symmetric and anti-symmetric (besides the empty relation in example 2.9).

3. Functions

Remark 3.1 (concept of function)

The concept of function is introduced in definition 2.3.

Definition 3.2 (types of functions)

A function  f : X → Y  is said to be injective if ∀ x₁,x₂ ∈ X, f(x₁) = f(x₂) ⇒  x₁ = x₂. In other words, x₁ ≠x₂ ⇒  f(x₁) ≠ f(x₂).
A function  f : X → Y  is said to be surjective, or onto, if ∀ y ∈ Y, ∃ x ∈ X,  y = f(x).
A function is said to be bijective if it is both injective and onto.

Question 3.3

Is any of the functions in example 2.4 injective ? Onto ? Bijective ?

Remark 3.4 (relevance of the domain and codomain)

The sets X and Y are an inseparable part of the concept of function (see definition 2.3). If we change one of them, the nature of the function may change. For instance, the function  f(x) = x², defined on ℝ with values in ℝ, is not injective nor onto. Explain why. If we change the codomain to [0,+∞[ we get a new function (having the same arithmetic expression x²) which is onto. On the other hand, the function x², defined on [0,+∞[ with values in ℝ, is injective but not onto. And finally the function x², defined on [0,+∞[ with values in [0,+∞[, is both injective and onto (so it is bijective).
Note also that we may choose other domains of definition. For instance, the function x², defined on ]-∞,0] with values in [0,+∞[, is also bijective.

Question 3.5 (codomain of x²)

What happens if we choose, for the function x² (see Remark 3.4), the domain of definition [0,+∞[ and the codomain ]-∞,0] ?

Answer

It makes no sense to consider a function like f : [0,+∞[ → ]-∞,0], f(x) = x². Such an object does not match the definition 2.3. For instance, there is no y ∈ ]-∞,0] such that y = 3².

Definition 3.6 (cartesian product of two functions)

Let  f : U → X  and  g : V → Y  be two functions. Define their cartesian product   f×g : U×V → X×Y  as  (f×g) (u,v) = (f(u),g(v)).

Definition 3.7 (image and inverse image of sets)

Let f : X → Y be a function and let A be a subset of X and B be a subset of Y.
We call image of A through f to the set f(A) = {f(x) : x ∈ A} ⊂ Y.
We call inverse image of B through f to the set f^-1(B) = {x ∈ X : f(x) ∈ B} ⊂ X.

Remark 3.8 (about the notation f^-1)

The notation f^-1 in Definition 3.7 does not imply that f  has inverse.

Question 3.9 (image and inverse image of empty set)

Let  f : A → B  be a function. Compute  f (∅).
Compute f^-1(∅).

Questions 3.10 (images of sets through x²)

Let f : ℝ → ℝ, f(x) = x².
a) Compute  f ({0}).
b) Compute  f ({1}).
c) Compute  f ({-1}).
d) Compute  f ([0,1]).
e) Compute  f ([0,1[).
f) Compute  f ([-1,1]).
g) Compute  f (]-1,1]).
h) Compute  f ([0,+∞[).
i) Compute  f (]-∞,0[).
j) Compute  f (ℝ).

Questions 3.11 (inverse images of sets through x²)

Let f : ℝ → ℝ, f(x) = x².
a) Compute  f^-1({0}).
b) Compute  f^-1({1}).
c) Compute  f^-1({-1}).
d) Compute  f^-1([0,1]).
e) Compute  f^-1([0,1[).
f) Compute  f^-1([-1,1]).
g) Compute  f^-1(]-1,1]).
h) Compute  f^-1([0,+∞[).
i) Compute  f^-1(]-∞,0[).
j) Compute  f^-1(]-∞,0]).
k) Compute  f^-1(]-∞,1[).
l) Compute  f^-1(]-∞,1]).
m) Compute  f^-1(ℝ).

Challenges 3.11.a (monotonicity of images)

Let  f : X → Y be a function.
a) Let A and B be two subsets of  X. If A ⊂ B then  f(A) ⊂ f(B)
b) Let  C and D be two subsets of Y. If C ⊂ D then  f^-1(C) ⊂ f^-1(D)

Questions 3.12 (union, intersection and complementary of images)

Let  f : X → Y be a function.
Let A and B be two subsets of  X. What can be said about  f (A∪B) ? About  f (A∩B) ? About  f (∁A) ?
Let 𝒜 be a family of subsets of  X. What can be said about  f (⋃𝒜) ? About  f (⋂𝒜) ?

Answers

f (A∪B) = f(A) ∪ f(B); f (A∩B) ⊂ f(A) ∩ f(B); if  f  is injective then f (A∩B) = f(A) ∩ f(B).

Questions 3.13 (union, intersection and complementary of inverse images)

Let  f : X → Y be a function.
Let  C and D be two subsets of Y. What can be said about  f^-1(C∪D) ? About  f^-1(C∩D) ? About  f^-1(∁C) ?
Let  𝒞 be a family of subsets of Y. What can be said about  f^-1(⋃𝒞) ? About  f^-1(⋂𝒞) ?

Answers

f^-1(C∪D) = f^-1(C) ∪ f^-1(D); f^-1(C∩D) = f^-1(C) ∩ f^-1(D).

Definition 3.14 (composition of functions)

Let  f : X → Y  and  g : Y → Z  be two functions. Note that the codomain of  f  is the domain of definition of g. We define the composition of  g  and  f  to be the function  h : X → Z  acting as  h(x) = g(f(x)). We use the notation h = g∘f. Note that the domain of  h is the domain of  f  and the codomain of  h is the codomain of  g.

Questions 3.15 (properties of the composed function)

If  f  and  g are injective, what can be said about  g∘f ?
If  f  and  g are onto, what can be said about  g∘f ?

Question 3.16 (image of a set through a composed function)

Let  f : X → Y  and  g : Y → Z  be two functions. Let A  be a subset of  X. What can be said about  (g∘f) (A) ?

Question 3.17 (inverse image of a set through a composed function)

Let  f : X → Y  and  g : Y → Z be two functions. Let C be a subset of Z. What can be said about (g∘f)^-1(C) ?

Definition 3.18 (inverse function)

Let f : X → Y and g : Y → X be two functions. Note that the codomain of f is the domain of definition of g and the codomain of g is the domain of definition of f. We say that g is the inverse function of f if g∘f = id_X (the identity function on X) and f∘g = id_Y (the identity function on Y). We use the notation g = f^-1.

Remark 3.19 (equivalent definitions of the inverse function)

Definition 3.18 can be re-written as : ∀x ∈ X, g(f(x)) = x  and   ∀y ∈ Y, f(g(y)) = y
It can also be re-written as : ∀x ∈ X, ∀y ∈ Y, y = f(x) ⇔ x = g(y)
Thus, computing the inverse of a given function f can be viewed as solving the equation y = f(x) in the unknown x (treating y as a parameter).

Challenge 3.20 (invertible implies bijective)

Prove that, if a function is invertible (that is, there is an inverse of it) then it is injective and onto (that is, it is bijective).

Answer

In the spirit of remark 3.19, we look at the equation y = f(x) in the unknown x (treating y as a parameter). The fact that f is bijective ensures that this equations has a unique solution, which we denote by x = g(y) or x = f^-1(y).

Challenge 3.21 (bijective implies invertible)

Prove that, if a function is injective and onto (that is, it is bijective) then it is invertible (that is, it has an inverse).

Examples 3.22 (inverse of x²)

See remark 3.4.
The function f : ℝ → ℝ, f(x) = x², is not invertible since it is not bijective.
The function f : [0,+∞[ → [0,+∞[, f(x) = x², is bijective, thus it has an inverse. How is its inverse called ?
The function f : ]-∞,0] → [0,+∞[, f(x) = x², is bijective, thus it has an inverse. How is its inverse called ?

Challenge 3.23 (inverse of a composition)

Let f : X → Y and g : Y → Z be two bijective functions. What can be said about the inverse of g∘f ?
Hint : use remark 3.19.

Answer

We look at the equation z = g(f(x)) and try to solve it with respect to the unknown x (treating z as a parameter). Since g is bijective, we first find an expression for f(x) which is f(x) = g^-1(z). Then, since f is bijective, we solve with respect to x and find that x = f^-1(g^-1(z)). We thus conclude that (g∘f)^-1 = f^-1∘ g^-1.

Question 3.24 (inverse of a cartesian product)

Let  f : U → X  and  g : V → Y  be two invertible functions. What can be said about the inverse of their cartesian product  f×g : U×V → X×Y ? See definition 3.6.

4. Equivalence relations, quotient sets

Definition 4.1 (equivalence relation)

A relation  R between a set  X and itself is called an equivalence relation if it is reflexive, symmetric and transitive (see definition 2.6).
When dealing with an equivalence relation, we often write  x~y instead of  xRy.

Examples 4.2 (equivalence relations)

a) In a population, the relation "x has the same age as y" is an equivalence relation.
b) In a population, the relation "x is a friend of y" is not an equivalence relation (see comments about friendship in remark 2.7).
c) In the set of all chemical elements, the relation "x has the same valence as y" is not an equivalence relation because the valence of an element depends on the molecule it is part of. For instance, phosphorus has a valence of 3 in phosphine (PH₃) and a valence of 5 in phosphorus pentachloride (PCl₅).
d) Let p be a natural number, p ≥ 2. On ℤ, the relation "x-y is a multiple of p" is an equivalence relation. It is called "equivalence modulo p" or "equality modulo p".
e) Let r be a real positive number. On ℝ, the relation "there is an integer number k such that x-y = kr" is an equivalence relation.
f) On ℝ, the relation "|x-y| ≤ 1" (which we can describe as "proximity") is not an equivalence relation.
g) On ℝ, the relation "x ≤ y" is not an equivalence relation.
h) On ℝ³, the relation "x has the same norm as y" is an equivalence relation.
i) Let L ⊂ ℝ³ be a straight line. Is the relation "x and y are equally far from the line L" an equivalence relation on ℝ³ ?
j) On ℝⁿ\{O}, the relation "x and y are colinear with O" is an equivalence relation.
k) On ℝⁿ\{O}, the relation "x and y are colinear with O and O is not between them" is an equivalence relation.
l) Let  X be a non-empty set and let 𝒜 be a partition of  X (definition 1.48). Define the relation "x and y belong to the same element of the partition 𝒜". Is this an equivalence relation on  X ?

Proposition 4.3 (relations defined as f(x) = f(y))

Let  X and Y  be two non-empty sets. Let  f : X → Y  be a function. For convenience, we shall assume  f  is onto (see definition 3.2). Then the relation  f(x) = f(y) is an equivalence relation on  X.
Many equivalence relations are defined in terms of equality of values of a certain function, see e.g. examples 4.2.a and 4.2.h. Actually, according to proposition 4.12, all equivalence relations can be described this way; see also remark 4.12.

Challenge 4.4

Find a set Y and a function f which describe, as in property 4.3, each of the equivalence relations in examples 4.2.a, 4.2.d, 4.2.e, 4.2.h, 4.2.i, 4.2.j, 4.2.k, 4.2.l.

Answers

The answers of challenge 4.14 apply here (take the quotient set and the canonical projection).

Definition 4.5 (class of equivalence)

Equivalence relations tend to create groups, or blocks, or "clusters".
More precisely : let X be a non-empty set and let ~ be an equivalence relation on X. Let

x

 ∈ X be an arbitrary element. We call class of equivalence of

x

to the set { y ∈ X :

x

 ~ y }. The class of equivalence of

x

can be denoted by

\hat{x}

; it is a subset of X.

Question 4.6 (class of equivalence viewed as inverse image)

For a relation defined as "equality of values of a certain function" like in property 4.3, how is the notion of class of equivalence related to the concept of inverse image of a set through a function (see definition 3.8) ?

Challenges 4.7 (describe the class of equivalence)

In examples 4.2.a, 4.2.d, 4.2.e, 4.2.h, 4.2.i, 4.2.j, 4.2.k pick an arbitrary element

x

 ∈ X and describe its class of equivalence

\hat{x}

Answers

In 4.2.a, the equivalence class of a ten-year-old child is the set of all children in the world of age ten.
In 4.2.d, choosing p = 2, the equivalence class of 3 is the set of all odd numbers. If we choose p = 5, the equivalence class of 0 is the set of all numbers divisible by 5.
In 4.2.e, if we choose a natural number for p, we obtain a concept similat to the relation in 4.2.d but on a larger set (ℝ rather than ℤ). If we choose e.g. p = 𝜋, the equivalence class of 1 is the set of all numbers of the form 1 + k𝜋 with k ∈ ℤ; it can be written as 1 + 𝜋ℤ.
In 4.2.h, the equivalence class of the origin is a set with only one point, the origin itself. The equivalence class of any other point is a sphere centered at the origin.
In 4.2.i, the equivalence class of a point belonging to L is L. The equivalence class of a point not belonging to L is a cylindrical surface around L.
In 4.2.j, the equivalence class of any point different from O is a straight line passing through the origin O.
In 4.2.k, the equivalence class of any point different from O is a semi-line starting at the origin O.

Definition 4.8 (quotient set)

Let  ~  be an equivalence relation on  X. Consider the set of all equivalence classes relative to the relation  ~. That is the set {

\hat{x}

x

; ∈ X }, which is a subset of 𝒫(X). This set is called quotient set of the set X with respect to the relation ~ and is denoted by  X/~. If we use the notation R instead of  ~, we may denote the quotient set by  X/R.

Challenge 4.9 (the quotient set is a partition)

Prove that the quotient set  X/~  is a partition of X (definition 1.48).

Definition 4.10 (canonical projection)

The application 𝜋 : X → X/~ defined by 𝜋(

x

) =

\hat{x}

is called canonical projection of the equivalence relation  ~.

Remark 4.11

The canonical projection is onto.
If, in proposition 4.3, we choose Y = X/~ and f = 𝜋, we obtain the equivalence relation we started with.

Proposition 4.12 (x ~ y ⇔ f(x) = f(y))

For a given equivalence relation, there is always an onto function  f  such that x ~ y ⇔ f(x) = f(y). To prove this, one can choose Y to be the quotient set and f to be the canonical projection; see definition 4.8, definition 4.10 and remark 4.11. Alternatively, one can choose a "representative element" in each equivalence class; this is done by applying the axiom of choice.
The set Y and the function f with this property are unique up to a bijection. That is, if Z is another set and g : X → Z is an onto function such that x~y ⇔ g(x) = g(y), then there exists a bijection 𝜑 : Y → Z such that g = 𝜑∘f. To prove this, one can use again remark 4.11.

Remark 4.13

An equivalence relation can be defined in three equivalent ways : through definition 4.1, through a partition of X (example 4.2.l) or through an onto function defined on X (proposition 4.3, remark 4.11, proposition 4.12).

Challenges 4.14 (describe the quotient set)

In examples 4.2.a, 4.2.d, 4.2.e, 4.2.h, 4.2.i, 4.2.j, 4.2.k, 4.2.l, describe the quotient set and the canonical projection.

Answers

In 4.2.a, the quotient set is made of slightly more than one hundred populational layers. It can be identified with (it is in bijection with) the set {0,1,2,3,...n} where n is a natural number slightly above 100. The canonical projection is simply the age of each individual.
In 4.2.d, the quotient set can be identified with { 0,1,2,...,p-1 }. The canonical projection is the remainder of the division by p.
In 4.2.e, the quotient set can be identified with the semi-open interval [0,r[.
In 4.2.h and 4.2.i, the quotient set can be identified with the set [0,+∞[. The canonical projection is simply the distance (to the origin in 4.2.h, to the line L in 4.2.i).
In 4.2.j, the quotient set is simply the set of all straight lines passing through the origin O and the canonical projection associates to each point x the line Ox.
In 4.2.k, the quotient set can be identified with the sphere S^n-1 and the canonical projection is 𝜋(x) =

\frac{x}{|| x ||}

.
In 4.2.l, the quotient set is 𝒜 itself and the canonical projection is the one in definition 4.10.

Remark 4.15 (quotient is reverse of product)

The name "quotient set" is chosen on purpose. In a certain sense, the quotient operation (between a set and an equivalence relation) is the reverse operation of the cartesian product.
More precisely, let A and B be two non-empty sets. Denote by  X  their cartesian product,  X = A×B, and consider the projection from  X onto A, 𝜋_A : X → A, 𝜋_A(x,y) = x. Denote by  ~  the equivalence relation defined by 𝜋_A in the spirit of proposition 4.3. In other words, (x₁,y₁) ~ (x₂,y₂) ⇔ x₁ = x₂. Then the quotient set X/~ can be identified with A.
This may be easier to visualize in a geometric context. Let A = [a,b] and B = [c,d] be two intervals in ℝ. Then X can be viewed as a rectangle in ℝ². The projection 𝜋_A associates to each point P = (x,y) its coordinate x on the horizontal axis A. The class of equivalence of a point P is the set of points having the same first cooordinate as P, that is, the vertical segment passing through P, drawn below in red. The set of these vertical segments can be identified with A.

5. Order relations

Definition 5.1 (order)

A relation  R  between a set  X  and itself is called an order (or partial order) if
a) R is reflexive,
b) R is anti-symmetric,
c) R is transitive.
See definition 2.6.
The pair (X,R) is called ordered set.
We will sometimes use the notation x ≤ y instead of xRy.

Examples 5.2

a) On ℕ, ≤ is an order.
b) On ℤ, ≤ is an order.
c) On ℝ, ≤ is an order.
d) Let  A be a set. On  𝒫(A)  (the family of all subsets of A), the inclusion is an order.

Remark 5.3

The strict inequality x < y between numbers is not an order in the sense of definition 5.1 because it is not reflexive.

Remark 5.3.a

Transitivity, together with anti-symmetry, implies that cycles are forbidden. That is, the only way for a chain of inequalities like x₁ ≤ x₂ ≤ ... ≤ x_n ≤ x₁ to happen is when the elements x_k are all equal. The game "rock paper scissors" is an example when a cycle can show up due to the lack of transitivity, see remark 2.7.

Remark 5.4

There is no canonical ordering of  ℂ.

Remark 5.5

The term "partial order" is intended to stress that not any two elements are comparable.
That is, in a partially ordered set X there may exist two elements x,y ∈ X such that neither xRy nor yRx hold. For instance, in  𝒫(A)  (example 5.2.d) there are sets B,C ⊂ A such that none of B or C is included in the other.
In contrast, in a totally ordered set (definition 5.6) any two elements are comparable.

Definition 5.6 (total order)

If, in an ordered set (X,R), for any two elements x,y ∈ X, either xRy or yRx holds, we say that X is totally ordered. We may also use the term linear order or chain.

Remark 5.7

Any subset of an ordered set inherits the order.
Any subset of a totally ordered set inherits the total order.

Definition 5.8

On the set ℝ², define the relation (x₁,y₁) ≤ (x₂,y₂)  ≡  x₁ ≤ x₂ and y₁ ≤ y₂.
Is this an order in the sense of definition 5.1 ? Is this a total order ?

Definition 5.9 (lexicographic order)

On the set ℝ², define the relation (x₁,y₁) ≤ (x₂,y₂)  ≡  x₁ < x₂ or (x₁ = x₂ and y₁ ≤ y₂).
Is this an order in the sense of definition 5.1 ? Is this a total order ?
This is called lexicographic order. It can be adapted to ℝⁿ or even to ℝ^ℕ (the set of all sequences of real numbers). It is similar to the alphabetic order encountered in a telephone list or in a dictionary.

Definition 5.10 (upper bound, lower bound)

Let (X,≤) be an ordered set and let  A  be a subset of  X. An element  M ∈ X  is called an upper bound for  A  if  ∀ a ∈ A, a ≤ M.
Similarly, an element  m ∈ X  is called a lower bound for A if  ∀ a ∈ A, m ≤ a.

Remark 5.11

Not any subset of an ordered set has upper (or lower) bounds. For instance, ℕ (as a subset of ℝ with the usual order) has no upper bound. ℤ (as a subset of ℝ with the usual order) has no lower bound and no upper bound.
When an upper (or lower) bound exists, it is usually not unique.

Definition 5.12 (maximum, minimum)

Let (X,≤) be an ordered set and let A be a subset of X. If M ∈ X is an upper bound for A and M ∈ A then M is called maximum of A. We use the notation max A. If m ∈ X is a lower bound for A and m ∈ A then m is called minimum of A. We use the notation min A.

Challenge 5.13

The minimum of a set, if it exists, is unique (prove). The maximum of a set, if it exists, is unique (prove).

Challenge 5.13.a (monotonicity of min and max)

If A ⊂ B and both have minima, then min A ≥ min B. If A ⊂ B and both have maxima, then max A ≤ max B.

Challenge 5.14

In ℝ² with the order introduced in definition 5.8, find the minimum and maximum of the following sets.
a) The square [0,1]².
b) The triangle of vertices (0,0),(1,0),(0.5,0.7).
c) The disk { (x,y) ∈ ℝ² : x²+y² ≤ 1 }.
d) The straight line { (x,y) ∈ ℝ² : x = y }.

Answers

a) minimum is (0,0), maximum is (1,1); b) minimum is (0,0), there is no maximum; c) there is no minimum nor maximum; d) an infinite straight line has no lower or upper bounds, so it has no minimum nor maximum

Challenge 5.15

Repeat challenge 5.14 with the lexicographic order.

Answers

a) minimum is (0,0), maximum is (1,1); b) minimum is (0,0), maximum is (1,0); c) minimum is (-1,0), maximum is (1,0); d) an infinite straight line has no lower or upper bounds, so it has no minimum nor maximum

Definition 5.16 (supremum, infimum)

In  ℝ with the usual order, consider a non-empty subset A. Consider the set B of all upper bounds of A. If B is not empty, then B has a minimum. This is a fundamental property of the set of real numbers. The minimum of B is called supremum of A. We use the notation sup A.
If B is empty (that is, if A has no upper bound) then, by convention, we say that the supremum of A is +∞.
The definition of the infimum is similar. We take the set of all lower bounds of A. If this set is not empty, it has a maximum which we call infimum of A. We use the notation inf A. If A has no lower bounds, we say that its infimum is -∞.
By convention, we say that the supremum of the empty set is -∞ and the infimum of the empty set is +∞.

Challenge 5.17

Let A be a non-empty subset of ℝ.
If A has a minimum, then it has a finite infimum and min A = inf A.
If A has a maximum, then it has a finite supremum and max A = sup A.
If inf A ∈ A then min A = inf A.
If sup A ∈ A then max A = sup A.

Challenge 5.18

There are non-empty sets A ⊂ ℝ which are bounded below (thus, they have a finite infimum) but inf A ∉ A. Prove that such a set does not have minimum. Provide examples.
Formulate and prove the analogous property for sets that do not have maximum. Provide examples.

Challenge 5.18.a (monotonicity of inf and sup)

If A ⊂ B then inf A ≥ inf B and sup A ≤ sup B.

Questions 5.19

Let A and B be two subsets of  ℝ.
a) What can be said of inf (A ∪ B) ?
b) What can be said of sup (A ∪ B) ?
c) What can be said of min (A ∪ B) ?
d) What can be said of max (A ∪ B) ?
e) What can be said of inf (A ∩ B) ?
f) What can be said of sup (A ∩ B) ?
g) What can be said of min (A ∩ B) ?
h) What can be said of max (A ∩ B) ?
i) What can be said of inf (A + B) ?
j) What can be said of sup (A + B) ?
k) What can be said of min (A + B) ?
l) What can be said of max (A + B) ?
Recall that A + B = { a+b : a ∈ A, b ∈ B }

Answers

a) inf (A ∪ B) = min { inf A, inf B };
b) sup (A ∪ B) = max { sup A, sup B };
c) if both A and B have minima, then A ∪ B has minimum and min (A ∪ B) = min { min A, min B };
d) if both A and B have maxima, then A ∪ B has maximum and max (A ∪ B) = max { max A, max B };
e) inf (A ∩ B) ≥ max { inf A, inf B };
f) sup (A ∩ B) ≤ min { sup A, sup B };

Metric spaces

6. Basic notions and properties, distance beetween sets, diameter

Definition 6.1 (distance, metric space)

Let X be a non-empty set. A function d : X × X → ℝ is called a distance on X (or a metric) if it satisfies the following properties :
a) ∀ x,y ∈ X, d(x,y) ≥ 0
b) ∀ x,y ∈ X, d(x,y) = d(y,x)
c) ∀ x ∈ X, d(x,x) = 0
d) ∀ x,y ∈ X, d(x,y) = 0  ⇒  x = y
e) ∀ x,y,z ∈ X, d(x,z) ≤ d(x,y) + d(y,z)
The pair (X,d) is called a metric space.

Remark 6.2 (triangular inequality)

Property 6.1.e is called triangular inequality. It formulates mathematically the intuitive idea that the path from point A to point C should be shorter than (or equal to) the distance from A to some intermediate point B plus the distance from point B to point C.

Remark 6.3 (metric on a finite set)

The set X in definition 6.1 may be finite. For instance, the following diagram shows a valid distance on a set with four elements.

Of course, the distance between any city and itself is zero (according to property 6.1.c); this information is not visible in the diagram above.

Thus, a metric space with a finite number of points can be seen as a weighted graph.

Question 6.4 (violation of triangular inequality)

If we change, in remark 6.3, the distance from London to Madrid to, say, 1704 km, this new function (shown below) is not a distance. Why ?

Challenge 6.5 (a metric space with one element)

If, in definition 6.1 we take an atomic set X (a set with one element only) then the distance d is uniquely defined. Why ?

Challenge 6.6

Prove, as a consequence of the triangular inequality, that ∀ x,y,z ∈ X, d(x,z) ≥ |d(x,y) - d(y,z)|

Answer

From property 6.1.e we infer that ∀ x,y,z ∈ X, d(x,y) ≥ d(y,z) - d(x,z). By switching the roles of x and y, we infer that ∀ x,y,z ∈ X, d(x,y) ≥ d(x,z) - d(y,z). These two inequalities can be re-written into one : ∀ x,y,z ∈ X, d(x,y) ≥ |d(x,z) - d(y,z)|.

Question 6.7 (the discrete distance)

Let X be a set. Define the function d(x,x) = 0, d(x,y) = 1 for x ≠ y. Is d a distance ?
This is called discrete distance.

Questions 6.8 (distances on ℝ)

a) Prove that d(x,y) = |x-y| is a distance on ℝ.
b) The function d(x,y) = |x²-y²| is not a distance on ℝ. Why ?
c) The function d(x,y) = (x-y)² is not a distance on ℝ. Why ?
d) Is the function d(x,y) = 

\frac{|x-y|}{xy}

a distance on ]0,+∞[ ?

Questions 6.9 (angles as distances)

a) Consider the set of all straight lines in ℝ² which pass through the origin. Is the angle between lines a distance on this set ?
b) Consider the set of all rays in ℝ² (half-lines) starting at the origin. Is the angle between rays a distance on this set ?
c) Consider the set of all straight lines in ℝ³ which pass through the origin. Is the angle between lines a distance on this set ?
d) Consider the set of all rays in ℝ³ (half-lines) starting at the origin. Is the angle between rays a distance on this set ?
e) Consider the set of all planes in ℝ³ which pass through the origin. Is the angle between planes a distance on this set ?

Answer

In all cases, the angle is a distance on the respective set.

Questions 6.10 (arithmetic operations between distances)

Let d₁ and d₂ be two distances on a set X.
a) Is d₁ + d₂ a distance ?
b) Is d₁ d₂ a distance ?
c) Is d₁ - d₂ a distance ?
d) Is d₁/d₂ a distance ?
e) Is d₁² + d₂² a distance ?
f) Is

\sqrt{{d_{1}}^{2} + {d_{2}}^{2}}

a distance ?
g) Is min {d₁,d₂} a distance ?
h) Is max {d₁,d₂} a distance ?

Answer

a) yes
b) no
c) no
d) no
e) no
f) yes
g) yes
h) no

Questions 6.11 (modified distance)

Let (X,d) be a metric space.
a) Is  

\frac{d (x, y)}{1 + d (x, y)}

  a distance on X ?
b) Is  min {1, d(x,y)}  a distance on X ?
c) Is  max {1, d(x,y)}  a distance on X ?
d) Is  d²(x,y)  a distance on X ?

Answer

a) yes
b) yes
c) no
d) no

Definition 6.12 (distance between sets)

Let A and B be two subsets of a metric space X. The distance between A and B is defined as dist (A,B) = inf { d(a,b), a ∈ A, b ∈ B }.
If one of the sets has only one element, say A = {x^⋆}, we use the notation dist (x^⋆,B) = dist ({x^⋆}, B) = inf { d(x^⋆,b), b ∈ B }.

Question 6.13 (zero distance between sets)

If A and B have common points, then dist (A,B) = 0  (prove). Is the reverse true ?

Answer

No. In ℝ (with the Euclidian distance), the intervals ]0,1[ and ]1,2[ have no common points, yet their distance is 0.

Question 6.14 (zero distance between a point and a set)

Let A be a subset of a metric space (X,d) and let x^⋆ be a point in X. If x^⋆ ∈ A then dist (x^⋆, A) = 0  (prove). Is the reverse true ?

Answer

No. In ℝ (with the Euclidian distance), the 0 does not belong to ]0,1[, yet their distance is 0.

Challenge 6.15

Does the triangular inequality hold for the distance between sets ? That is, if A, B and C are three subsets of a metric space, can we prove that dist (A,C) ≤ dist (A,B) + dist (B,C) ?

Answer

No. In ℝ (with the Euclidian distance), dist ([0,1],[1,2]) = 0 and dist ([1,2],[2,3]) = 0, yet dist ([0,1],[2,3]) > 0.

Challenge 6.16

In the spirit of of challenge 6.15, prove (or disprove) triangular inequalities for a point and two sets, as well as for two points and a set.

Remark 6.17

Let (X,d) be a metric space. The set 𝒫(X) of all subsets of X, endowed with the distance defined in definition 6.12, is not a metric space. Why ?

Answer

See challenge 6.15.

Definition 6.18 (Euclidian distance)

On ℝⁿ we define the Euclidian distance (the usual distance given by the Pythagorean theorem) as d(x,y) =

\sqrt{{(x_{1} - y_{1})}^{2} + {(x_{2} - y_{2})}^{2} + ... + {(x_{n} - y_{n})}^{2}}

Prove that this quantity satisfies all properties in definition 6.1.

Hint

See question 6.10.f.

Challenges 6.19

In ℝ² with the Euclidian distance, compute the distance
a) between the unit circle and the line x+2y = 5.
b) between the parabola y = x² and the point (1,0).
c) between the hyperbola xy = 1 and the origin.
d) between the hyperbola xy = 1 and the union of the two axes.
e) between the region xy ≤ 1 and the disk (x-5)² + (y-3)² ≤ 1.
f) between the region xy ≤ 1 and the disk (x-5)² + (y-4)² ≤ 1.

Definition 6.20 (diameter)

We define the diameter of a metric space (X,d) as diam X = sup { d(x,y) : x,y ∈ X  }. Note that the diameter may be infinite.

Question 6.21 (zero diameter)

Is there a metric space of diameter zero ?

Answer (difficulty level 1)

Yes, the (not very interesting) space with one point only.

Definition 6.22 (metric subspace)

Let A be a subset of a metric space (X,d_X). The function d : X×X → ℝ, when restricted to A×A, provides a distance d_A on the set A. The metric space (A,d_A) is called a subspace of (X,d_X). We say that the distance d_A on A is induced by the distance on X.
This can be expressed as d_A = d_X ∘ (i×i), where i is the inclusion of A into X  (i : A → X, i(x) = x) and i×i is the cartesian product between i and itself; see definition 3.6.

Remark 6.23 (extending concepts to subsets)

Using the notion of metric subspace (definition 6.22), we can extend many concepts from a metric space to subsets of a metric space. For instance, we shall call diameter of a subset A ⊂ X to the diameter of A as a metric space with the distance induced from X.

Challenges 6.24

In ℝ² with the Euclidian distance, compute the diameter of
a) a disk.
b) a circle.
c) a rectangle.
d) a triangle.
e) a straight line.

Answer

a) twice the radius
b) twice the radius
c) the length of the diagonal
d) the largest length among the three sides
e) infinity

Challenge 6.25

Let (X,d) be a metric space; consider two subsets A ⊂ B ⊂ X. Prove that diam A ≤ diam B.

Hint

Use challenge 5.18.a.

Question 6.26

Let A and B be two subsets of a metric space X. What can be said about the diameter of A ∪ B ? About the diameter of A ∩ B ?

Answers (difficulty level 3)

diam (A ∪ B) ≤ diam A + diam B + dist (A,B)
diam (A ∩ B) ≤ min { diam A, diam B } (see challenge 6.25)

Definition 6.27 (bounded space, bounded set)

A metric space is said to be bounded if its diameter is finite. In the spirit of remark 6.23, a subset of a metric space is said to be bounded if its diameter is finite.

Challenges 6.28

Prove that
a) ℝ with the Euclidian distance is not bounded.
b) ℝ² with the Euclidian distance is not bounded.
c) [0,+∞[ with the distance introduced in question 6.8.d is not bounded.

Challenges 6.29

a) Prove that an atomic set is bounded.
b) Prove that a union between two bounded sets is bounded.
c) Prove that a union of a finite family of bounded sets is bounded.
d) Use properties a) and c) to prove that a finite set is bounded.

Answers (difficulty level a:1, b:2, c:2, d:1)

a) the diameter of an atomic set is zero
b) see challenge 6.26

Challenge 6.30

Let (X,d) be an arbitrary metric space (bounded or not). Prove that X, with the distance introduced in question 6.11.a, is bounded. Repeat with the distance introduced in question 6.11.b.

Remark 6.31 (sets connected by piecewise C¹ paths)

In the sequel, we shall focus on subsets X of ℝⁿ which are connected by piecewise C¹ paths, meaning that any two points of X are connected by a path within X. In this section, by "path" we mean a piecewise C¹ curve r : [a,b] → ℝⁿ (here, r : [a,b] → X).
Note that this notion of path is more restrictive than the one in definition 16.11 because here we need to be able to compute the length of a path by means of a line integral: len (r) = ∫_a^b ‖r'(t)‖ dt. 16.11

Definition 6.32 (geodesic distance)

Let X ⊂ ℝⁿ be a set connected by piecewise C¹ paths. For any x,y ∈ X, define d_g (x,y) as the infimum of all lengths of all possible paths linking, within X, x to y. Prove that d_g is a distance on X. It is called geodesic distance.

Remark 6.33

The geodesic distance (definition 6.32) is often different from the Euclidian distance induced from ℝⁿ (definition 6.22). See, however, challenge 6.34.

Challenge 6.34

Prove that, if X ⊂ ℝⁿ is a convex set, then the geodesic distance on X is equal to the distance induced from ℝⁿ.

Challenges 6.35

a) Let X ⊂ ℝ² be the unit circle, X = S¹. Compute d ((0,1),(1,0)) and d_g ((0,1),(1,0)) where d is the distance induced from ℝ² and d_g is the geodesic distance.
b) Let X ⊂ ℝ² be the annulus X = { (x,y) ∈ ℝ² : 1 ≤ x² + y² ≤ 4 }. Compute d_g((0,1),(1,0)) and d_g((0,2),(2,0)).
c) Let X ⊂ ℝ² be the annulus X = { (x,y) ∈ ℝ² : 1 ≤ x² + y² ≤ 2 }. Compute d_g((0, $\sqrt{2}$ ),( $\sqrt{2}$ ,0)).
d) Let X ⊂ ℝ² be the annulus X = { (x,y) ∈ ℝ² : 1 < x² + y² ≤ 2 }. Compute d_g((0, $\sqrt{2}$ ),( $\sqrt{2}$ ,0)).
e) Let X ⊂ ℝ² be the annulus X = { (x,y) ∈ ℝ² : 9 ≤ x² + y² ≤ 16 }. Compute d_g ((0,4),(4,0)).

7. Isometries

Definition 7.1 (transported distance)

Let (X,d_X) be a metric space and let Y be a set. Consider a bijection  f : X → Y between X and Y. Define d_Y : Y × Y → ℝ as d_Y (y₁, y₂) = d_X (f^-1(y₁), f^-1(y₂)). That is, d_Y = d_X ∘ (f^-1 × f^-1), see definition 3.6. Then d_Y is a distance on Y (prove). It is called the transported distance from X through  f.

Remark 7.2

If the transported distance of d_X through  f  is d_Y, then the transported distance of d_Y through  f^-1 is d_X. That's because (f × f)^-1 = f^-1× f^-1; see question 3.24.

Remark 7.3

Consider the sets X = Y = ]0, +∞[ and the bijection  f : X → Y, f(x) = 1/x. Then the Euclidian distance on X, transported through  f on Y, produces the distance described in question 6.8.d.

Definition 7.4 (isometry)

Let (X,d_X) and (Y,d_Y) be two metric spaces. A bijection  f : X → Y is called isometry between X and Y if it preserves distances, that is, if ∀ x₁, x₂ ∈ X, d_Y (f(x₁), f(x₂)) = d_X(x₁, x₂).
Two metric spaces (X,d_X) and (Y,d_Y) are said to be isometric if there is an isometry between them.

Remark 7.5 (equivalent definition of isometry)

An equivalent definition of the concept of isometry is : ∀ y₁, y₂ ∈ Y, d_Y (y₁, y₂) = d_X(f^-1(y₁), f^-1(y₂)).
Still another equivalent definition of the same concept is : the transported distance of d_X through  f  is d_Y.

Remark 7.7 (isometry between a space and itself)

There are isometries between a metric space and itself. In other words : in definition 7.1 we can take (X,d_X) = (Y,d_Y).

Challenges 7.10 (isometries between Euclidian spaces)

a) Describe all possible isometries f : ℝ → ℝ with the Euclidian distance.
b) Describe all possible isometries f : ℝ² → ℝ² with the Euclidian distance.
c) Describe all possible isometries f : ℝ³ → ℝ³ with the Euclidian distance.

Remark 7.11 (isometric spaces are indistinguishable)

If there is an isometry between two metric spaces, then these spaces have exactly the same properties. For instance, they have the same diameter. If A and B are two subsets of X, then dist_X(A,B) = dist_Y(f(A),f(B)).

Challenges 7.12 (isometries between spaces of different dimensions)

Considering, in each case, the Euclidian distance,
a) describe the isometries between ℝ and ℝ².
b) describe the isometries between ℝ² and ℝ³.
c) describe the isometries between ℝ and ℝ³.

Answer

No isometries exist between different powers of ℝ.

Remark 7.13 (restriction of an isometry is an isometry)

If  f  is an isometry between X and Y and A ⊂ X is a subset of X, then f, restricted to A, is an isometry between A and  f(A), viewed as metric subspaces of X, respectively Y.
On the other hand, if an isometry between A and B is given, there is no guarantee that this isometry is the restriction of some isometry between X and Y. And, if it is, there is no guarantee that the isometry between X and Y is uniquely defined. That is, there may exist several isometries between X and Y which, when restricted to A, produce the same isometry between A and B.

Challenges 7.14 (isometries between subsets of ℝ²)

Considering, in each case, the Euclidian distance inherited from ℝ², describe all isometries between
a) the disk of center (0,0) and radius 1 and the disk of center (0,0) and radius 2
b) the disk of center (0,0) and radius 1 and the square [0,1]²
c) the square [0,1]² and the rectangle [0,1] × [0,2]
d) the square [0,1]² and the triangle of vertices (0,0), (1,0), (0,1)

Answer

a) there are no isometries (the diameters are not equal)
b) there are no isometries (the diameters are not equal)
c) there are no isometries (the diameters are not equal)
d) Although the diameters are equal, there are no isometries. Several arguments can be used to prove this. For instance, the maximum distance between two points in the square is attained for two pairs of points. The maximum distance between two points in the triangle is attained for only one pair of points.

Definition 7.15 (group of isometries)

The set of all isometries between a metric space (X,d) and itself, endowed with the composition operation, is a group (prove).

Challenge 7.16 (find the group of isometries)

For each of the metric subspaces of ℝ² represented below (with the Euclidian metric), compute the group of isometries.
a) a straight line
b) a circle
c) a rectangle
d) a square
e) an ellipse
f) an egg-like shape
g) the digit 8
h) the letter A
i) the letter F

Answer

a) all translations and reflections of the line
b) all rotations (with center at the origin) and reflections (with respect to a line passing through the origin)
c) a group with four elements: the identity, the 180º rotation and two reflections
d) a group with eight elements, called dihedral group of order 8, containing the identity and three rotations, as well as four reflections.
e) the same as for the rectangle
f) a group with two elements, containing the identity and one reflection
g) depending on the details of the shape of the glyph, it could be the same as for the ellipse or the same as for the egg-like shape
h) the same as for the egg-like shape
i) the trivial group, containig the identity only

Remark 7.17

Items 7.18 - 7.30 assume that the reader is familiar with the notion of neighbourhood of a point in a metric space. See definition 8.14.

Definition 7.18 (local isometry)

Let (X,d_X) and (Y,d_Y) be two metric spaces. A bijection  f : X → Y is called local isometry if for any x^⋆ ∈ X there is a neigbourhood V of x^⋆ and a neighbourhood W of  f(x^⋆) such that the restriction of f to V is an isometry between V and W.

Remark 7.19

Consider the metric spaces X = ]-1,0[ ∪ ]0,1[ and X = ]0,1[ ∪ ]2,3[ with the Euclidian distance inherited from ℝ. Prove there is no isometry between X and Y. Prove there is a local isometry between X and Y.

Remark 7.20 (global isometry is local isometry)

An isometry in the sense of definition 7.4 (which we may call "global isometry") is also a local isometry.

Questions 7.21

Described below are several pairs of metric spaces X, Y. For each such pair, is there a (global) isometry ? Is there a local isometry ?
a) X, Y ⊂ ℝ², X = B((0,0),1) ∪ B((1,1),0.2), Y = B((0,0),0.2) ∪ B((1,1),1).
four disks

b) X, Y ⊂ ℝ², X = B((0,0),1) ∪ B((1,1),0.2), Y = B((0,0),1) ∪ B((2,0),0.2).
four disks

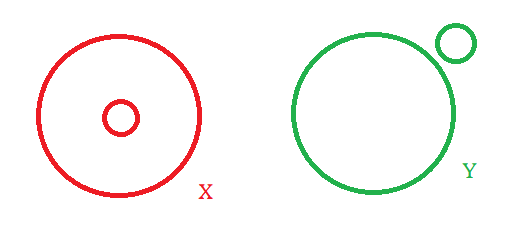
c) A = {(x,y) ∈ ℝ² : d((x,y),(0,0)) = 1}, B = {(x,y) ∈ ℝ² : d((x,y),(0,0)) = 0.2}, C = {(x,y) ∈ ℝ² : d((x,y),(1,1)) = 0.2}, X = A ∪ B, Y = A ∪ C.
four circles

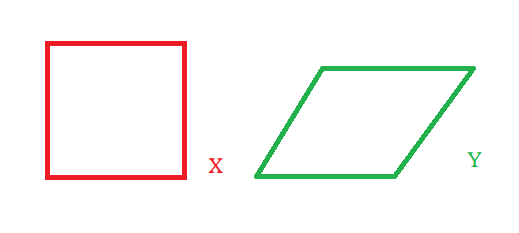
d) X = [(0,0),(1,0)] ∪ [(1,0),(1,1)] ∪ [(1,1),(0,1)] ∪ [(0,1),(0,0)], X = [(0,0),(1,0)] ∪ [(1,0),(1.5, $\sqrt{3}$ /2)] ∪ [(1.5, $\sqrt{3}$ /2),(0.5, $\sqrt{3}$ /2)] ∪ [(0.5, $\sqrt{3}$ /2),(0,0)].
square and parllelogram

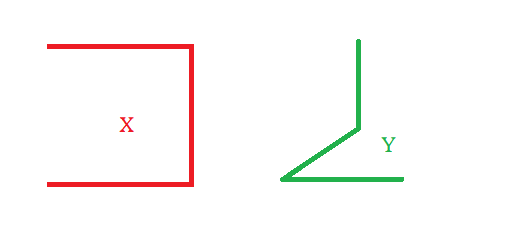
e) X ⊂ ℝ², X = [(0,1),(0,0)] ∪ [(0,0),(1,0)] ∪ [(1,0),(1,1)], Y ⊂ ℝ³, Y = [(1,0,0),(0,0,0)] ∪ [(0,0,0),(0,1,0)] ∪ [(0,1,0),(0,1,1)].
skeleton

Questions 7.22 (unfolding angles)

a) Consider X ⊂ ℝ², X = [(0,1),(0,0)] ∪ [(0,0),(1,0)] with the Euclidian distance and Y ⊂ ℝ, Y = [0,2] with the Euclidian distance. Is there an isometry between X and Y ? Is there a local isometry ?
angle

b) Consider X ⊂ ℝ³, X = { (x,y,z) ∈ ℝ³ : x ≥ 0, z = 0 } ∪ { (x,y,z) ∈ ℝ³ : x = 0, z ≥ 0 } (a union of two half-planes) with the Euclidian distance inherited from ℝ³ and Y = ℝ² with the Euclidian distance. Is there an isometry between X and Y ? Is there a local isometry ?
two planes

c) Consider X ⊂ ℝ³, X = { (x,y,z) ∈ ℝ³ : x = 0, y ≥ 0 , z ≥ 0 } ∪ { (x,y,z) ∈ ℝ³ : x ≥ 0, y = 0, z ≥ 0 } ∪ { (x,y,z) ∈ ℝ³ : x ≥ 0, y ≥ 0, z = 0 } (a union of three quarters of plane) with the Euclidian distance inherited from ℝ³ and Y = ℝ² with the Euclidian distance. Is there an isometry between X and Y ? Is there a local isometry ?
three planes

d) Answer to the same questions a), b) and c) but taking the geodesic distance on X.

Definition 7.23 (locally isometric spaces)

We say that two metric spaces (X,d_X) and (Y,d_Y) are locally isometric if for any x^⋆ ∈ X there is a y^⋆ ∈ Y and there is a neighbourhood V of x^⋆ and there is a neighbourhood W of  y^⋆ and there is an isometry  f : V → W (in the sense of definition 7.4, V and W being viewed as metric subspaces of  X, respectively of Y) such that  f(x^⋆) = y^⋆.
The reverse should also hold true : for any  y^⋆ ∈ Y there is an x^⋆ ∈ X  having isometric neighbourhoods.

Question 7.24

a) Is the interval ]0,1[, with the Euclidian distance, locally isometric to ℝ ?
b) Is the interval [0,1[, with the Euclidian distance, locally isometric to ℝ ?
c) Is the unit circle S¹ = { (x,y) ∈ ℝ² : x²+y² = 1 }, with the Euclidian distance inherited from ℝ², locally isometric to ℝ ?
d) Is the unit circle S¹ = { (x,y) ∈ ℝ² : x²+y² = 1 }, with the geodesic distance, locally isometric to ℝ ?

Question 7.25

Consider (the exterior face of) a cylinder in ℝ³, S = { (x,y,z) ∈ ℝ³ : x²+y² = 1 }.
a) Is S, with the Euclidian distance, locally isometric to ℝ² ?
b) Is S, with the geodesic distance, locally isometric to ℝ² ?

Question 7.26

Consider (the exterior face of) a cone in ℝ³, S = { (x,y,z) ∈ ℝ³ : x²+y² = z², z > 0 }.
a) Is S, with the Euclidian distance, locally isometric to ℝ² ?
b) Is S, with the geodesic distance, locally isometric to ℝ² ?

Question 7.27

Consider (the exterior face of) a sphere in ℝ³, S = { (x,y,z) ∈ ℝ³ : x²+y²+z² = 1 }.
a) Is S, with the Euclidian distance, locally isometric to ℝ² ?
b) Is S, with the geodesic distance, locally isometric to ℝ² ?

Remark 7.28

If there exists a local isometry between two metric spaces X and Y (in the sense of definition 7.18) then X and Y are locally isometric in the sense of definition 7.23. However, the reverse is not true, see challenge 7.29.

Challenge 7.29

Show that, for the spaces in questions 7.24.a, 7.24.b, 7.24.d, 7.25.b, 7.26.b, there is no local isometry between them in the sense of definition 7.18 (although the spaces are locally isometric in the sense of definition 7.23).

Challenge 7.30

Some metric spaces X are "homogeneous" in the sense that for any x^⋆ and x^⋆⋆ in X, there is a neighbourhood V of x^⋆ and a neighbourhood W of x^⋆⋆ which are isometric. Provide examples.

Answer (difficulty level 5)

One example is ℝⁿ (or any open set of it), another example is the sphere Sⁿ ⊂ ℝⁿ⁺¹ (or any open set of it).

8. Open balls, neighbourhoods, open sets

Definition 8.1 (open ball)

Let (X,d) be a metric space. Let r be a real number, r > 0. Let x^⋆ ∈ X be a point in X. We call open ball of center x^⋆ and radius r to the set { x ∈ X : d (x, x^⋆) < r }. We denote the open ball by B (x^⋆, r).

Challenges 8.2

For the metric space in remark 6.3, compute the open ball
a) with center in Lisbon and radius 2000 km.
b) with center in Madrid and radius 2000 km.
c) with center in Paris and radius 1000 km.
d) with center in London and radius 300 km.
e) with center in London and radius 2500 km.

Question 8.3 (diameter of an open ball)

What can be said of the diameter of an open ball ?

Answer (difficulty level 2)

The diameter of an open ball is less than or equal to twice the radius. There are examples when this inequality is strict.

Challenge 8.4

Compute the diameter of each ball in challenges 8.2.

Question 8.5

Take two open balls having the same radius but different centers. Are their diameters equal ?

Answer (difficulty level 2)

Not always.

Challenge 8.6 (balls in angular distance)

For each metric space in challenges 6.9, pick a point x^⋆ at your choice and a number r > 0 at your choice and describe the open ball B(x^⋆,r).

Challenge 8.7 (balls in the geodesic distance)

For each metric space in challenges 6.35, pick a point x^⋆ at your choice and a number r > 0 at your choice and describe the open ball B(x^⋆,r).

Challenge 8.8

Prove that a set A ⊂ X is bounded if and only if there exists an x^⋆ ∈ X and an r > 0 such that A ⊂ B(x^⋆,r).

Answer (difficulty level 2)

Suppose A is bounded, thus d = diam A is finite. Pick any x^⋆ ∈ X. Then it is easy to prove that A is included in the closed ball centered at x^⋆ and with radius d. Take an r slightly greater than d and the result is proven.
If A is included in an open ball of radius r, challenge 6.25 and question 8.3 imply that diam A ≤ 2r, thus A is bounded.

Definition 8.9 (closed ball)

Let (X,d) be a metric space. Let r ∈ ℝ, r > 0. Let x^⋆ ∈ X. We call closed ball of center x^⋆ and radius r to the set { x ∈ X : d (x,x^⋆) ≤ r }.

Question 8.10 (diameter of a closed ball)

What can be said of the diameter of a closed ball ?

Answer (difficulty level 2)

The diameter of a closed ball is less than or equal to twice the radius. There are examples when this inequality is strict.

Challenge 8.11

For each item in challenges 8.2, compute the corresponding closed ball.

Question 8.12

Is the diameter of an open ball equal to the diameter of the closed ball with the same center and same radius ?

Answer (difficulty level 2)

The diameter of an open ball is less than or equal to the diameter of the corresponding closed ball. There are examples when this inequality is strict.

Question 8.13

Take two closed balls having the same radius but different centers. Are their diameters equal ?

Answer (difficulty level 2)

Not always.

Definition 8.14 (neighbourhood)

Let  x^⋆ ∈ X  be a point and  A ⊂ X  be a subset of a metric space (X,d). We say that A is a neighbourhood of x^⋆ if there exists r > 0 such that  B(x^⋆,r) ⊂ A.
Of course if  A is a neighbourhood of x^⋆ then  x^⋆ ∈ A.

Remark 8.15 (a ball is a neighbourhood of its center)

An open ball is a neighbourhood of its center. A closed ball is a neighbourhood of its center.

Question 8.16

Let x^⋆ ∈ X  and let A ⊂ X  be a neighbourhood of x^⋆.
If  B is another set such that  A ⊂ B ⊂ X, does this imply that  B  is a neighbourhood of  x^⋆, too ?

Answer (difficulty level 1)

Yes.

Challenge 8.17

Let x^⋆ ∈ X and let  A ⊂ X  be a neighbourhood of x^⋆. Prove that there is a closed ball centered at x^⋆ and included in A.
In other words, in definition 8.14 we could have used a closed ball rather than an open ball, and still obtain the same concept of neighbourhood.

Questions 8.18 (union, intersection of neighbourhoods)

Let  A and  B  be two neighbourhoods of a point  x^⋆ ∈ X.
a) Is A ∪ B a neighbourhood of  x^⋆ ?
b) Is A ∩ B a neighbourhood of  x^⋆ ?
Let 𝒜  be a finite family of neighbourhoods of a point  x^⋆∈ X.
c) Is ⋃𝒜  a neighbourhood of  x^⋆ ?
d) Is ⋂𝒜  a neighbourhood of  x^⋆ ?
Let 𝒜  be a family (possibly infinite, possibly uncountable) of neighbourhoods of a point  x^⋆ ∈ X.
e) Is ⋃𝒜  a neighbourhood of  x^⋆ ?
f) Is ⋂𝒜  a neighbourhood of  x^⋆ ?

Answers (difficulty level a:1, b:2, c:1, d:3, e:1, f:3)

a) yes
b) yes
c) yes
d) yes
e) yes
f) no

Definition 8.19 (open set)

A subset A ⊂ X of a metric space (X,d) is said to be open if it is a neighbourhood of each x^⋆ ∈ A.
In other words, a set A ⊂ X is open if  ∀ x^⋆ ∈ A, ∃ r > 0, B (x^⋆, r) ⊂ A.
Of course the radius r of the ball depends on x^⋆.

Remark 8.20 (void set and entire space are open)

The entire space X  is an open subset of (X,d).
By applying formal logic to definition 8.19 we see that the empty set is always open, too (see remark 1.13).

Challenge 8.21

Describe all open sets of the metric space in Remark 6.3.

Answer (difficulty level 2)

In that metric space, all sets are open.

Remark 8.22

The concept of open set describes a relation between a set  A and the surrounding space  X ; see examples 8.23.

Examples 8.23

a) Consider the metric space ℝ with the Euclidian distance. The interval  I = [0,1[ is not open in this space (prove).
b) Consider the metric space [0, +∞[ with the Euclidian distance (it can be viewed as a metric subspace of ℝ). The interval  I = [0,1[ is open in this space (prove).

Answers (difficulty level a:2, b:3)

a) In ℝ, [0,1[ is not a neighbourhood of 0.
b) In [0, +∞[, [0,1[ is a neighbourhood of 0. Actually, it is an open ball of center 0 and radius 1. See challenge 8.24.a

Challenge 8.25 (intervals in ℝ)

Consider the metric space ℝ with the Euclidian distance
a) Let a,b ∈ ℝ, a < b. Prove that the interval ]a,b[ is an open set.
b) Let a,b ∈ ℝ, a < b. Prove that the interval [a,b] is not a open set.
c) Let a ∈ ℝ. Prove that ]a,+∞[ is an open set.
d) Let a ∈ ℝ. Prove that [a,+∞[ is not an open set.

Challenge 8.26

a) Prove that an open ball (definition 8.1) is an open set in the sense of definition 8.19.
b) Is a closed ball (definition 8.9) an open set in the sense of definition 8.19 ?

Answer (difficulty level a:3, b:3)

a) Let x^⋆ ∈ X and r > 0. Let x ∈ B(x^⋆,r). Define ε = r - dist(x^⋆,x) > 0. Then B(x,ε) ⊂ B(x^⋆,r) (use the triangular inequality to prove this inclusion) thus B(x^⋆,r) is a neighbourhood of x so B(x^⋆,r) is open.
b) Not always.

Questions 8.28 ( union, intersection, complementary of open sets)

Let A and B be two open subsets of a metric space  (X,d)
a) Is A ∪ B open ?
b) Is A ∩ B open ?
Let  A  be an open subset of a metric space  (X,d).
c) Is ∁A = X \ A open?
Let 𝒜 be a finite family of open subsets of a metric space (X,d).
d) Is ⋃𝒜  open ?
e) Is ⋂𝒜  open ?
Let 𝒜  be a family (possibly infinite, possibly uncountable) of open subsets of a metric space (X,d).
f) Is ⋃𝒜  open ?
g) Is ⋂𝒜  open ?

Challenge 8.29

Let A ⊂ X be an open set. Prove that, for each x^⋆ ∈ A, there is a closed ball centered at x^⋆ and included in A.
In other words: in Definition 8.19 we could have used closed balls rather than open balls, and still obtain the same concept of open set.

Question 8.30

Consider the metric space ℚ with the Euclidian distance (it can be viewed as a metric subspace of ℝ). Is the set { x ∈ ℚ : 2 ≤ x² ≤ 3 } open in this space ?

Answer (difficulty level 3)

Yes.

Challenge 8.31

Let (X,d) be a metric space.
a) Prove that for any two distinct points x,y ∈ X  there are two disjoint open balls centered at x, respectively y. Formally :  ∀ x,y ∈ X, x ≠ y ⇒ ∃ r₁, r₂ > 0, B(x,r₁) ∩ B(y,r₂)= ∅.
b) Prove that the statement in challenge 8.31.a can be reformulated with r₁= r₂ . Formally : ∀ x,y ∈ X, x ≠ y ⇒ ∃ r > 0, B(x,r) ∩ B(y,r)= ∅.
c) Prove that in challenge 8.31.b one can replace open balls by closed balls.
d) Challenges 8.31.a-8.31.c can be reformulated as : any two distinct points in a metric space have mutually disjoint neighbourhoods.

Answers (difficulty level a:3, b:3, c:3)

For a) and b), we can take r = r₁= r₂= dist(x,y) / 2. For c) we take a slightly lower value, for instance r = dist(x,y) / 3.

Challenge 8.32 (inequalities between distances)

Let (X,d) be a metric space. Let A be a subset of X. Consider r > 0.
a) Is the set { x ∈ X : dist (x,A) < r } open ?
Let B be another subset of X.
b) Is the set { x ∈ X : dist (x,A) < dist (x,B) } open ?

Challenge 8.35 (open subsets of a given set)

Let A be a subset of a metric space (X,d). Consider the family 𝒪 of all subsets of  A which are open in  X. This set is ordered with the inclusion relation.
Prove that 𝒪 has a maximum element.
Note that this family is never empty since ∅ ∈ 𝒪. It may happen that 𝒪 = { ∅ }; in this case, the maximum element is ∅.

Remark 8.36

If we reverse the inclusion relation in challenge 8.35, the answer becomes negative. That is, take 𝒪 the family of all open sets in  X which contain  A; ordered with the inclusion, this family may have no minimum element.
Note that this family is never empty since  X ∈ 𝒪.

Definition 8.37 (interior of a set)

The largest open set included in a given set  A (the maximum element in challenge 8.35) is called the interior of  A and is denoted by int A, or

\overset{\circ}{A}

. Points in  

\overset{\circ}{A}

are called interior points of  A.
Note that

\overset{\circ}{A}

may be void; see challenge 8.35.

Remark 8.38

A set  A is open if and only if  A = 

\overset{\circ}{A}

Challenge 8.39

Prove that a point x^⋆ is interior to a set A if and only if  ∃ r > 0,  B(x^⋆,r) ⊂ A.

Challenge 8.40 (monotonicity of interior)

Prove that if  A and  B  are two sets such that  A ⊂ B then  

\overset{\circ}{A}

 ⊂ 

\overset{\circ}{B}

Challenges 8.41 (interior of subsets of ℝ)

In ℝ with the Euclidian distance, compute the interior of
a) {0}
b) [0,1]
c) [0,1[
d) ℕ
e) ℚ
f) ℝ \ { 0 }
g) ℝ \ ℚ
h) { 1, 1/2, 1/3, 1/4,...}

Challenges 8.42 (interior of subsets of ℝ²)

In ℝ² with the Euclidian distance, compute the interior of
a) { (0,0) }
b) ℝ² \ { (0,0) }
c) ℝ × {0}
d) the line segment [ (0,0), (1,1) ]
e) the square [0,1]²
f) [0, +∞[ × ℝ

Question 8.43 ( interior of union, of intersection)

Let  A and  B  be two subsets of a metric space (X,d). What can be said of the interior of  A ∪ B ? What can be said of the interior of  A ∩ B ?

9. Convergent sequences, closed sets, equivalent metrics

Definition 9.1 (convergent sequence)

Let (X,d) be a metric space. Let (x_n) be a sequence of points in X. We say that x_n  converges to a point x^⋆ ∈ X if ∀ε > 0, ∃N ∈ ℕ, ∀n ≥ N, d(x_n,x^⋆) < ε.
We use the notation x_n → x^⋆ or lim_n→+∞ x_n = x^⋆.
The point x^⋆ is called limit of the sequence x_n

Remark 9.2 (N depends on ε)

In definition 9.1, N depends of course on ε and could be denoted by N(ε).

Remark 9.3 (two players)

The chain of quantifiers in definition 9.1 can be better understood by imagining a competition between two players. The first player provides a small value of ε in order to make it difficult for the second player to find an N satisfying the requirements. If the second player finds a suitable N, the first player has the right to choose a new, smaller, value of ε and the game goes on indefinitely.
If the first player wins, that is, if there is an ε > 0 for which the second player cannot provide a suitable N, then the sequence x_n does not converge to x^⋆. If the first player never wins (which, after an infinite number of exchanges between the players, can be interpreted as "the second player wins"), then the sequence x_n converges to x^⋆.
This idea of a chain of quantifiers as a competition between two players is present in remark 1.25.

Remark 9.4

Definition 9.1 can be interpreted as follows. As n increases, the points x_n get closer and closer to x^⋆. More precisely : the points x_n  get as close to x^⋆ as we wish, and then remain at this distance or closer (for ∀n ≥ N). The word "we" in the previous statement can be interpreted as "the first player"; see remark 9.3.

Remark 9.5

The inequality d(x_n,x^⋆) < ε in definition 9.1 can be re-written as x_n ∈ B(x^⋆,ε); see definition 7.1.

Challenge 9.6 (uniqueness of the limit)

Prove that, in Definition 9.1, x^⋆ is uniquely associated to the sequence x_n. More precisely, prove that if x_n → x^⋆ and x_n → x^⋆⋆ then x^⋆ = x^⋆⋆. In other words: in a metric space, a sequence cannot have two different limits.

Challenge 9.7 (equivalent definitions of convergence)

Which of the logical expressions below is equivalent to definition 9.1 ?
a) ∀ε > 0 ∃N ∈ ℕ ∀n ≥ N d(x,x^⋆) ≤ ε
b) ∀ε > 0 ∃N ∈ ℕ ∀n > N d(x,x^⋆) < ε
c) ∀ε > 0 ∃N ∈ ℕ ∀n > N d(x,x^⋆) ≤ ε
d) ∀ε ≥ 0 ∃N ∈ ℕ ∀n ≥ N d(x,x^⋆) < ε
e) ∀ε ≥ 0 ∃N ∈ ℕ ∀n ≥ N d(x,x^⋆) ≤ ε
f) ∀ε ≥ 0 ∃N ∈ ℕ ∀n > N d(x,x^⋆) < ε
g) ∀ε ≥ 0 ∃N ∈ ℕ ∀n > N d(x,x^⋆) ≤ ε

Remark 9.8 (definition of convergence using neighbourhoods)

Definition 9.1 can be rewritten as: for any neighbourhood V of x^⋆ there is an N ∈ ℕ such that ∀n ≥ N, x_n ∈ V; see definition 8.14 and remark 9.5.

Definition 9.9 (bounded sequence)

Let (x_n) be a sequence of points in a metric space (X,d). We say that (x_n) is a bounded sequence if the set {x_n} ⊂ X of its terms is bounded in the sense of definition 6.27.

Challenge 9.10 (convergent implies bounded)

Prove that a convergent sequence is necessarily bounded.

Answer (difficulty level 3)

Let x_n → x^⋆; by definition, ∀ε > 0, ∃N(ε) ∈ ℕ, ∀n ≥ N(ε), d(x_n,x^⋆) < ε. Take ε = 1 (or any other positive value, for that matter). This implies that, for ∀n ≥ N(1), x_n belongs to the ball of center x^⋆ and radius 1, which is a bounded set. The first terms x₁, x₂, ..., x_N(1)-1 form a finite set which is bounded by challenge 6.29.d. Apply challenge 6.29.b to conclude that the entire sequence is bounded.

Question 9.11 (convergence in a metric subspace)

Let (X,d) be a metric space, and let  Y ⊂ X be a metric subspace; see definition 6.22.
a) If (y_n) is a sequence of points in Y converging (in Y) towards a point y^⋆ ∈ Y, then is it true that y_n → y^⋆ in X ?
b) If (x_n) is a sequence of points in Y, converging (in X) towards a point x^⋆ ∈ Y, then is it true that x_n → x^⋆ in Y ?
c) Is there a sequence in Y which is convergent in X but does not converge in Y ?

Answer (difficulty level a:1, b:1, c:2)

Assertions a and b are true, as one sees by merely checking the definition.
As for c, the only situation when a sequence may converge in X but not in Y is when x_n ∈ Y, x_n → x^⋆ with x^⋆ ∈ X\Y.

Question 9.12

a) In [0,1] (as a metric subspace of ℝ with the Euclidian distance), does the sequence 1/n converge ?
b) In ]0,1[ (as a metric subspace of ℝ with the Euclidian distance), does the sequence 1/n converge ?

Question 9.13

Consider the sequence of numbers (x_n) defined recursively by x₁ = 1, x_n+1 = 

\frac{{x_{n}}^{2} + 2}{2 x_{n}}

a) Does this sequence converge in ℝ with the Euclidian distance?
b) Does this sequence converge in ℚ, as a subspace of ℝ with the Euclidian distance?

Challenge 9.14

For the metric space in remark 6.3, find a convergent sequence; find also a sequence which does not converge.

Challenge 9.15 (convergence of a subsequence)

Let (x_n) be a sequence in a metric space (X,d) and let (x_{n_k}) be a subsequence. How does the convergence of (x_n) relate to the convergence of (x_{n_k}) ?

Challenge 9.16

Let (x_n) and (y_n) be two sequences in a metric space (X,d) and consider the sequence (z_n) obtained by alternating terms of (x_n) with terms of (y_n), that is, z_2n = x_n, z_2n+1 = y_n. How does the convergence of (x_n) and (y_n) relate to the convergence of (z_n) ?

Remark 9.17

Definition 9.1 is equivalent to d(x_n,x^⋆) → 0 when n → +∞, in ℝ with the Euclidian distance.

Question 9.18

Let (x_n) be a sequence in a metric space (X,d) and let x^⋆, z ∈ X be two points
a) If x_n → x^⋆ in X, does it imply d(x_n,z) → d(x^⋆,z) in ℝ ?
b) If d(x_n,z) → d(x^⋆,z) in ℝ, does it imply x_n → x^⋆ in  X ?

Question 9.19

Let (x_n) be a sequence in a metric space (X,d) and let x^⋆ ∈ X be a point with the following property : ∀z ∈ X, d(x_n,z) → d(x^⋆,z). Does this imply x_n → x in  X ?

Question 9.20

Let (x_n) and (y_n) be two sequences in a metric space (X,d).
a) If both x_n and y_n converge to the same point x^⋆ ∈ X, does this imply d(x_n,y_n) → 0 in ℝ ?
b) If x_n → x^⋆ in  X and d(x_n,y_n) → 0 in ℝ, does this imply y_n → x^⋆ in  X ?

Definition 9.21 (closed set)

A subset F of a metric space (X,d) is said to be closed if, for any sequence (x_n) of points in F, if the sequence converges to some x^⋆ ∈ X then x^⋆ ∈ F.

Remark 9.22

The empty set ∅, as well as the entire space X, are closed sets.

Challenge 9.23

Describe all closed sets of the metric space in Remark 6.3.

Challenge 9.24 (complementary of an open set is closed)

Prove that a subset F of a metric space (X,d) is closed if and only if its complementary is open; see Definition 8.19.

Remark 9.25

The term "closed set" was chosen on purpose. A set F is closed when no sequence in F can "exit" F by passing to the limit; if a sequence converges then its limit belongs to F, too. Together with challenge 9.24, this provides a justification for the choice of the term "open set" to refer to the complementary of a closed set.

Remark 9.26

If a set is not open, this does not mean it is closed. If a set is not closed, this does not mean it is open.
There are sets which are simultaneously open and closed; see remarks 8.20 and 9.22 and example 9.27.b.
On the other hand, there are sets which are neither open nor closed; see example 9.27.a.

Example 9.27

a) Let X = ℝ with the Euclidian metric. In this metric space, the set ]2,3] is neither open nor closed.
b) Let X = [0,1] ∪ ]2,3] ∪ ]5,6[ with the Euclidian metric. In this metric space, the sets [0,1], ]2,3] and ]5,6[ are simultaneously open and closed.

Challenge 9.28

a) Prove that a closed ball (definition 8.9) is a closed set in the sense of definition 9.21.
b) Is an open ball (definition 8.1) a closed set in the sense of definition 9.21 ?

Questions 9.29 ( union, intersection, complementary of closed sets)

Let A and B be two closed subsets of a metric space  (X,d)
a) Is A ∪ B closed ?
b) Is A ∩ B closed ?
Let  A  be a closed subset of a metric space  (X,d).
c) Is ∁A = X \ A closed ?
Let 𝒜 be a finite family of closed subsets of a metric space (X,d).
d) Is ⋃𝒜  closed ?
e) Is ⋂𝒜  closed ?
Let 𝒜  be a family (possibly infinite, possibly uncountable) of closed subsets of a metric space (X,d).
f) Is ⋃𝒜  closed ?
g) Is ⋂𝒜  closed ?

Challenge 9.30 (intervals in ℝ)

Consider the metric space ℝ with the Euclidian distance
a) Let a,b ∈ ℝ, a < b. Prove that the interval [a,b] is a closed set
b) Let a,b ∈ ℝ, a < b. Prove that the interval ]a,b[ is not a closed set.
c) Let a,b ∈ ℝ, a < b. Prove that the interval [a,b[ is neither open nor closed.
d) Let a ∈ ℝ. Prove that ]a,+∞[ is not a closed set.
e) Let a ∈ ℝ. Prove that [a,+∞[ is a closed set.

Remark 9.31

The concept of closed set describes a relation between a set F and the surrounding space X; see examples 9.32. See also remark 8.22.

Examples 9.32

a) Consider the metric space X = ℝ with the Euclidian distance. In X, the set F = ]0,1] is not closed (prove).
b) Consider the metric space Y = ]0, +∞[ with the Euclidian distance. In Y, the set F = ]0,1] is closed (prove).

Question 9.33

Consider the metric subspace ℚ with the Euclidian distance (it can be viewed as a metric subspace of ℝ). Is the set { x ∈ ℚ : 2 < x² < 3 } closed in this space ?

Question 9.34 (distance between two closed disjoint sets)

If E and F are two closed subsets of a metric space (X,d) such that E ∩ F = ∅, does this imply dist (E,F) > 0 ? Compare with question 6.13.

Question 9.35 (distance between a point and a closed set)

If F is a closed subset of a metric space (X,d) and x^⋆ ∈ X \ F, does this imply dist (x^⋆, F) > 0 ? Compare with question 6.14.

Challenge 9.36 (inequalities between distances)

Let (X,d) be a metric space. Let A be a subset of X. Consider r > 0.
a) Is the set { x ∈ X : dist (x,A) ≤ r } closed ?
Let B be another subset of X.
b) Is the set { x ∈ X : dist (x,A) ≤ dist (x,B) } closed ?

Definition 9.37 (clopen set)

A subset A of a metric space is said to be clopen if it is simultaneously closed and open.
See example 9.27.b.

Challenge 9.38 (closed sets containing a given set)

Let A be a subset of a metric space (X,d). Consider the family ℱ of all closed sets F ⊂ X containing A. This family is an ordered set with the inclusion relation.
Prove that ℱ has a minimum element.
Note that this family is not empty since X ∈ ℱ. It may happen that ℱ = { X }; in this case, the minimum element is X.

Remark 9.39

If we reverse the inclusion relation in challenge 9.38, the answer becomes negative. That is, take ℱ the family of all subsets of  A which are closed in  X; ordered with the inclusion, this family may have no maximum element.
Note that this family is never empty since ∅ ∈ ℱ.

Definition 9.40 (closure of a set)

The smallest closed set containing A (challenge 9.38) is called the closure of A and is denoted by A.

Remark 9.41

A set A is closed if and only if A = A.

Challenge 9.42

Prove that x^⋆ ∈ A if and only if dist (x^⋆, A) = 0.

Challenge 9.43

Prove that x^⋆ ∈ A if and only if there exists a sequence (x_n) of elements of A converging to x^⋆.

Challenge 9.44 (closure of subsets of ℝ)

In ℝ with the Euclidian distance, compute the closure of
a) {0}
b) ℕ
c) ]0,1[
d) [0,1[
e) ℚ
f) ℝ \ {0}
g) ℝ \ ℚ
h) {1, 1/2, 1/3, 1/4,...}

Challenge 9.45 (closure of subsets of ℝ²)

In ℝ²with the Euclidian distance, compute the closure of
a) {(0,0)}
b) ℝ²\{(0,0)}
c) ]0,+∞[ × ℝ
d) ℝ × {0}
e) the square ]0,1[ ²
f) ℝ × ℚ
g) ℚ × ℚ

Remark 9.46

The closure of a set depends on the surrounding space. For instance, in the space X = [0,1], the closure of A = ]0,1[ is [0,1]. However, in the space Y = ]0,1], the closure of A = ]0,1[ is ]0,1]. See also Remark 9.31.

Challenge 9.47 (monotonicity of closure)

Prove that if  A and  B  are two sets such that  A ⊂ B then  A ⊂ B.

Question 9.48 (closure of union, of intersection)

Let  A and  B  be two subsets of a metric space (X,d). What can be said of the closure of  A ∪ B ? What can be said of the closure of  A ∩ B ?

Definition 9.49 (boundary of a set)

Let  A be a subset of a metric space (X,d). We call boundary of A, sometimes denoted by ∂A, to the difference A \ 

\overset{\circ}{A}

Remark 9.50

A set is closed if and only if it contains its boundary.
A set is open if and only if it is disjoint of its boundary.
A set is clopen if and only if it has empty boundary.

Definition 9.51 (dense set)

A subset A of a metric space (X,d) is called dense in X if A = X.
Provide examples.

Challenge 9.52

Prove that the property stated below is equivalent to the density of A :
For any (non-empty) open set B ⊂ X, A ∩ B ≠ ∅.

Question 9.53 (complementary of a dense set)

How can the property of a set being dense be expressed in terms of the complementary set ?

Definition 9.54 (equivalent distances)

Consider a set  X and two distances d₁ and d₂ on  X. We say that d₁ and d₂ are equivalent if the convergent sequences defined by d₁ are exactly the same as those defined by d₂. In other words, if x_n → x^⋆ in d₁ is equivalent to x_n → x^⋆ in d₂.

Challenge 9.55

If d₁ and d₂ are equivalent distances on  X, then a set is open relatively to d₁ if and only if it is open relatively to d₂. The same holds for the concepts of closed set, of interior, of closure, of dense set.

Challenge 9.56

The reverse of challenge 9.55 is also true. Given two distances on a set  X, if the open sets are the same then the distances are equivalent. If the closed sets are the same then the distances are equivalent. Thus, the concept of equivalent distances can be defined in different ways : the convergent sequences are the same, the open sets are the same, the closed sets are the same. We could even express it as : the neighbourhoods are the same.

Remark 9.57 (metric and topologic concepts and properties)

As we see, there are many concepts and properties which are invariant when we switch from a distance to another, equivalent, one. These concepts and properties are topologic in nature. We have already met some topologic concepts : convergent sequence, neighbourhood, open set, interior of a set, closed set, closure of a set, dense set. Other topologic concepts will be studied in sections 13 - 17 of this textbook.
We have also met concepts whose nature is not topologic; they are expressed in terms of distances and they may change if we modify the distance, even towards an equivalent distance. Some examples are : distance between points, diameter of a set, bounded set, distance between a point and a set, distance bewteen two sets.

Challenge 9.58

Prove that, if the set  X is finite, any two distances are equivalent.

Challenge 9.59

Prove that the distance introduced in question 6.8.d is equivalent to the Euclidian distance inherited from ℝ.

Challenge 9.60

Prove that, if (X,d) is a metric space, the quantities  

\frac{d}{1 + d}

  and  min {1, d}  are distances equivalent to d. See question 6.11.

Remark 9.61

Challenges 6.30 and 9.60 show that the diameter of a metric space is not a topologic concept. Thus, the concept of bounded space (or bounded set) is not topologic in nature.

Remark 9.62

A metric property often implies a topologic property. After all, the very definition 9.1 of convergence is expressed in metric terms (it uses the distance). It is rare for a topologic property to imply a metric one; challenges 9.10 and 9.42 show such cases.

Question 9.63 (dist (x,A) = 0 in equivalent distances)

Let d₁ and d₂ be two equivalent distances on a set  X. Let x^⋆ be an element of  X and A be a subset of  X. If dist (x^⋆,A) = 0 in (X,d₁), can we prove that dist (x^⋆,A) = 0 in (X,d₂) ?

Question 9.64 (dist (A,B) = 0 in equivalent distances)

Let d₁ and d₂ be two equivalent distances on a set  X. Let A and B be two subsets of  X. If dist (A,B) = 0 in (X,d₁), can we prove that dist (A,B) = 0 in (X,d₂) ?

10. Cauchy sequences, complete metric spaces

Definition 10.1 (Cauchy sequence)

Let (X,d) be a metric space (definition 6.1). Let (x_n) be a sequence of points in X. We say that (x_n) is a Cauchy sequence if ∀ 𝜀 > 0, ∃ N ∈ ℕ, ∀ m,n ≥ N, d(x_n,x_m) < 𝜀.

Remark 10.2 (N depends on 𝜀)

In definition 10.1, N depends of course on 𝜀 and could be denoted by N(𝜀). See also remark 9.2.

Remark 10.3

The definition 9.1 of convergent sequence involves an element x^⋆ exterior to the sequence. In contrast, the definition 10.1 of Cauchy sequence is expressed only in terms of the elements of the sequence.

Remark 10.4

The chain of quantifiers in definition 10.1 can be imagined as a competition between two players, in the spirit of remark 9.3.

Remark 10.5

Definition 10.1 can be interpreted as follows. As n increases, the points x_n of the sequence get closer and closer to each other. See also remark 9.4.

Question 10.6 (equivalent definition of Caychy sequence)

Which of the logical expressions below is equivalent to definition 10.1 ?
a) ∀ 𝜀 > 0, ∃ N ∈ ℕ, ∀ m,n ≥ N, d(x_n,x_m) ≤ 𝜀.
b) ∀ 𝜀 > 0, ∃ N ∈ ℕ, ∀ m,n > N, d(x_n,x_m) < 𝜀.
c) ∀ 𝜀 > 0, ∃ N ∈ ℕ, ∀ m,n > N, d(x_n,x_m) ≤ 𝜀.

Challenge 10.7 (Cauchy implies bounded)

Prove that if (x_n) is a Cauchy sequence then it is bounded (definition 6.27).

Challenge 10.8 (subsequence of a Cauchy sequence)

Let (x_n) be a sequence in a metric space (X,d) and let (x_{n_k}) be a subsequence. How does the property of (x_n) being Cauchy relate to the property of (x_{n_k}) being Cauchy ?

Challenge 10.10

Let (x_n) and (y_n) be two sequences in a metric space (X,d).
If both (x_n) and (y_n) are Cauchy sequences, prove that (d(x_n,y_n)) is a Cauchy sequence in ℝ.
Compare with question 9.20.

Questions 10.11

a) If a sequence (x_n) is convergent, does this imply that it is Cauchy ?
b) If a sequence (x_n) is Cauchy, does this imply that it is convergent ?
It should be noted that the second assertion is inherently more difficult to prove than the first one since we need to prove the existence of an element x^⋆ which does not appear in definition 10.1.

Answer

b) is false; there are Cauchy sequences which do not converge; see examples 10.12.

Examples 10.12 (Cauchy sequences which do not converge)

Prove that the sequences described below are Cauchy but do not converge.
a) In X = ]0,+∞[ with the Euclidian metric, x_n = 

\frac{1}{n}

 .
b) In X = ℚ with the Euclidian metric, define (x_n) recursively by x₁ = 1, x_n+1 = 

\frac{{x_{n}}^{2} + 2}{2 x_{n}}

 . Prove that this sequence is Cauchy but does not converge.

Challenge 10.13

Let (x_n) be a Cauchy sequence. Assume there exists a subsequence of (x_n) which is convergent. Prove that (x_n) is convergent.

Question 10.14 (Cauchy sequence in a metric subspace)

Let (X,d) be a metric space and let Y ⊂ X be a metric subspace, see definition 6.19. Let (y_n) be a sequence of points in Y. If (y_n) is Cauchy in X, does this imply that (y_n) is Cauchy in Y ? What about the other way around ?

Remark 10.15

The situations under consideration in questions 8.10 and 10.14 can be summarized as follows. The property "a sequence converges to a certain point" is intrinsic, does not describe a relation to the surrounding space. Likewise, the property of a sequence being Cauchy is intrinsic, does not depend on the surrounding space.
The property of a sequence being convergent only depends on the surrounding space because it may happen that the limit point belongs to a certain metric space but not to a given subspace, see question 9.11. This does not happen for the property of a sequence being Cauchy because this property does not involve an element exterior to the sequence; see remark 10.3.

Definition 10.16 (complete space)

We say that a metric space (X,d) is complete if any Cauchy sequence in  X is convergent in  X.
More precisely : if, for any Cauchy sequence (x_n) there exists a point x^⋆ ∈ X such that x_n → x^⋆ in  X.

Questions 10.17 (which spaces are complete ?)

Among the metric spaces below, which are complete ?
a) the space introduced in Remark 6.3
b) ℕ with the Euclidian distance
c) ℤ with the Euclidian distance
d) ℚ with the Euclidian distance
e) [0,+∞[ with the Euclidian distance
f) ]0,+∞[ with the Euclidian distance
g) [0,1] with the Euclidian distance
h) ]0,1[ with the Euclidian distance
i) ℝ with the Euclidian distance
j) ℝ\{0} with the Euclidian distance
k) ℝ\ℚ with the Euclidian distance
l) ℂ with the Euclidian distance

Remark 10.18

Since the notion of Cauchy sequence is not topologic in nature, the notion of complete space is also not topologic. More precisely : there may exist two equivalent metrics d₁ and d₂ on a set X such that (X,d₁) is complete and (X,d₂) is not.
Provide examples.

Challenge 10.19

Let  X be a complete metric space and  F ⊂ X be a closed subset. Prove that  F, as a subspace of  X, is complete.
This gives a quick positive answer to questions 10.17.a, 10.17.b, 10.17.c, 10.17.e, 10.17.g (if we assume 10.17.i).

Challenge 10.20

Let  X be a metric space and F ⊂ X be a subset. If  F (with the metric induced from  X) is complete, then  F is closed in  X.
This gives a quick negative answer to questions 10.17.f, 10.17.h and 10.17.j. Actually, also applies to questions 10.17.d and 10.17.k.

Definition 10.21 (completed space)

Let (

\tilde{X}

\tilde{d}

) be a metric space and let (X,d) be a metric subspace of it. If

\tilde{X}

is complete and X is dense in

\tilde{X}

then

\tilde{X}

is called the completed space of  X. See definitions 9.51 and 10.16.

Remark 10.22 (ℝ is the completed space of ℚ)

ℝ is complete and ℚ is dense in ℝ, so ℝ is the completed space of ℚ.
This is one possible definition of the concept of real number.

Challenge 10.23 (uniqueness of completed space)

For a given metric space  X, the completed space is unique up to an isometry.
More precisely : let  Y be a metric space such that  X is a subspace of  Y; let  Z be a metric space such that  X is a subspace of  Z. Denote by i_Y : X → Y the inclusion of X in Y and by i_Z : X → Z the inclusion of X in Z If both Y and Z are complete and X is dense in Y and X is dense in Z then there exists an isometry h : Y → Z such that h∘ i_Y = i_Z.
Note that, in the above, we do not state the existence of a completed space (this is postponed to challenge 10.24).

Challenge 10.24 (existence of a completed space)

For any metric space (X,d), a completed metric space (

\tilde{X}

\tilde{d}

) exists (definition 10.21).

11. Normed spaces

Remark 11.1 (vector space, linear dependence, base)

We assume the reader is acquainted with the notions of vector space, linear dependence (and independence) of vectors, base.
All vector spaces in this textbook are considered over the field of real numbers.

Definition 11.2 (norm)

Let  X be a vector space. A function n : X → ℝ is called a norm if
a) ∀ x ∈ X, n(x) ≥ 0
b) ∀ x ∈ X, n(x) = 0 ⇒ x=0
c) ∀ x,y ∈ X, n(x+y) ≤ n(x)+n(y) (subadditivity)
d) ∀ x ∈ X, ∀ λ ∈ ℝ, n(λx) = |λ|n(x) (positive homonegenity)
We often use the notation ||x|| instead of n(x).

Challenge 11.3

A consequence of property 11.2.d is that n(0) = 0.

Remark 11.4 (semi-norm)

If, from definition 11.2, we drop property b), we obtain the notion of semi-norm.

Challenge 11.5 (modulus is norm)

Prove that n : ℝ → ℝ, n(x)=|x| (the absolute value of x) is a norm.

Challenge 11.6 (norms on ℝⁿ)

Prove that the quantities below are norms on ℝⁿ :
a) ||x||_∞ = max { |x₁|, |x₂|, ... |x_n| } (the infinity norm)
b) ||x||₂ = ( x₁² + x₂² + ... + x_n² )^1/2 (the Euclidian norm, or two-norm)
c) ||x||₁ = |x₁| + |x₂| + ... + |x_n| (the one-norm)
d) for a given p >1, ||x||_p = ( |x₁|^p + |x₂|^p + ... + |x_n|^p )^1/p (the p-norm)

Questions 11.7 (skew norms on ℝ²)

a) Is max { |x₁|, 2|x₂| } a norm on ℝ² ?
b) Is |x₁| + 2|x₂| a norm on ℝ² ?
c) Is

\sqrt{{x_{1}}^{2} + 2 {x_{2}}^{2}}

a norm on ℝ² ?
d) Is

\sqrt{{x_{1}}^{2} + {x_{2}}^{2} - x_{1} x_{2}}

a norm on ℝ² ?
e) Is

\sqrt{{x_{1}}^{2} + {x_{2}}^{2} + 3 x_{1} x_{2}}

a norm on ℝ² ?

Remark 11.8 (a norm induces a distance)

If X is a vector space and n is a norm on X, then d(x,y) = n(x-y) is a distance on X.

Remark 11.9

On a vector space X, there are distances not originating from a norm.
Provide examples.

Questions 11.10 (norms on function spaces)

a) Is sup_x∈]0,1[ |f(x)| a norm on C(]0,1[) (the space of continuous functions on ]0,1[) ?
b) Is max_x∈[0,1] |f(x)| a norm on C([0,1]) (the space of continuous functions on [0,1]) ?
c) Is ∫₀¹ |f(x)| dx a norm on C(]0,1[) (the space of continuous functions on ]0,1[) ?
d) Is ∫₀¹ |f(x)| dx a norm on C([0,1]) (the space of continuous functions on [0,1]) ?
e) Is (∫₀¹ |f(x)|² dx)^1/2 a norm on C(]0,1[) (the space of continuous functions on ]0,1[) ?
f) Is (∫₀¹ |f(x)|² dx)^1/2 a norm on C([0,1]) (the space of continuous functions on [0,1]) ?

Definition 11.11

Let a < b be two real numbers. A function  f : ]a,b[ → ℝ is said to have compact support if there is an 𝜀 > 0 such that  f = 0 on ]a,a+𝜀[ and on ]b-𝜀,b[.

Remark 11.12

Some of the quantities in questions 11.10 are not norms simply because those quantities (e.g. integrals) are infinte for functions  f  which are continuous on ]0,1[. Such functions may be unbounded. In order to get finite quantities, we may add the assumption that  f  is bounded. Another possibility is to assume that the functions have compact support (definition 11.12) :
a) max_x∈[0,1] |f(x)| is a norm on C_b([0,1]) (the space of continuous bounded functions on [0,1]).
b) max_x∈]0,1[ |f(x)| is a norm on C_c(]0,1[) (the space of continuous functions on ]0,1[ with compact support).
c) ∫₀¹ |f(x)| dx is a norm on C_b(]0,1[) (the space of continuous bounded functions on ]0,1[).
d) ∫₀¹ |f(x)| dx is a norm on C_c(]0,1[) (the space of continuous functions on ]0,1[ with compact support).
e) (∫₀¹ |f(x)|² dx)^1/2 is a norm on C_b(]0,1[) (the space of continuous bounded functions on ]0,1[).
f) (∫₀¹ |f(x)|² dx)^1/2 is a norm on C_c(]0,1[) (the space of continuous functions on ]0,1[ with compact support).
g) ∫₀¹ |f(x)| dx is a norm on the space of C¹ functions on ]0,1[ which are bounded and whose first derivative is bounded.
h) ∫₀¹ |f(x)| dx is a norm on C¹_c(]0,1[) (the space of C¹ functions on ]0,1[ with compact support).
i) (∫₀¹ |f(x)|² dx)^1/2 is a norm on the space of C¹ functions on ]0,1[ which are bounded and whose first derivative is bounded.
j) (∫₀¹ |f(x)|² dx)^1/2 is a norm on C¹_c(]0,1[) (the space of C¹ functions on ]0,1[ with compact support).
k) ∫₀¹ (|f(x)|+|f'(x)|) dx is a norm on the space of C¹ functions on ]0,1[ which are bounded and whose first derivative is bounded.
l) ∫₀¹ (|f(x)|+|f'(x)|) dx is a norm on C¹_c(]0,1[) (the space of C¹ functions on ]0,1[ with compact support).
m) (∫₀¹ (|f(x)|²+|f'(x)|²) dx)^1/2 is a norm on the space of C¹ functions on ]0,1[ which are bounded and whose first derivative is bounded.
n) (∫₀¹ (|f(x)|²+|f'(x)|²) dx)^1/2 is a norm on C¹_c(]0,1[) (the space of C¹ functions on ]0,1[ with compact support).

Questions 11.13

a) Is ∫₀¹ |f'(x)| dx a norm on the space of C¹ functions on ]0,1[ which are bounded and whose first derivative is bounded ?
b) Is ∫₀¹ |f'(x)| dx a norm on C¹_c(]0,1[) (the space of C¹ functions on ]0,1[ with compact support) ?
c) Is (∫₀¹ |f'(x)|² dx)^1/2 a norm on the space of C¹ functions on ]0,1[ which are bounded and whose first derivative is bounded ?
d) Is (∫₀¹ |f'(x)|² dx)^1/2 a norm on C¹_c(]0,1[) (the space of C¹ functions on ]0,1[ with compact support) ?

Challenge 11.13⋆

Prove that, in a normed space, any ball is convex (may it be an open ball or a closed ball). Is it necessarily strictly convex ?

Definition 11.14 (inner product)

Let  X  be a vector space. A function p : X × X → ℝ is called inner product on X  if
a) ∀ x,y ∈ X, p(x,y) = p(y,x)
b) ∀ x^⋆ ∈ X, the map y ↦ p(x^⋆,y) is linear.
c) ∀ x ∈ X, p(x,x) ≥ 0
d) ∀ x ∈ X, p(x,x) = 0 ⇒ x=0

Challenge 11.15

A consequence of properties 11.14.a and 11.14.b is : ∀ y^⋆ ∈ X, the map x ↦ p(x,y^⋆) is linear.

Definition 11.16 (bilinear form)

A function with two arguments which is linear in each argument (when we keep the other argument frozen) is called a bilinear form.

Examples 11.17 (inner products on function spaces)

a) ∫₀¹ f(x)g(x) dx is an inner product on C_b(]0,1[) (the space of continuous bounded functions on ]0,1[).
b) ∫₀¹ f(x)g(x) dx is an inner product on C_c(]0,1[) (the space of continuous functions on ]0,1[ with compact support).
c) ∫₀¹ f(x)g(x) dx is an inner product on the space of C¹ functions on ]0,1[ which are bounded and whose first derivative is bounded.
d) ∫₀¹ f(x)g(x) dx is an inner product on C¹_c(]0,1[) (the space of C¹ functions on ]0,1[ with compact support).
e) ∫₀¹ (f(x)g(x)+f'(x)g'(x)) dx is an inner product on the space of C¹ functions on ]0,1[ which are bounded and whose first derivative is bounded.
f) ∫₀¹ (f(x)g(x)+f'(x)g'(x)) dx is an inner product on C¹_c(]0,1[) (the space of C¹ functions on ]0,1[ with compact support).

Remark 11.18 (inner product on a complex vector space)

In this textbook, all vector spaces are real (remark 11.1). For a complex vector space, we must change definition 11.14 accordingly. p will take complex values rather than real. In property 11.14.a, p(y,x) must be equal to the complex conjugate of p(x,y). Consequently, in challenge 11.15 we get not a linear map but an antilinear one. Also, property 11.14.c must be interpreted as : p(x,x) is real and ≥ 0. Definition 11.16 must also be changed accordingly, which leads us to the concept of sesquilinear form.

Challenge 11.19

If  p is an inner product on a vector space  X, the mapping n(x) =

\sqrt{p (x, x)}

is a norm on  X.

Challenge 11.20

In a space with inner product, any ball is strictly convex (may it be an open ball or a closed ball).

Question 11.21

In challenge 11.19 one builds a norm from an inner product. Is the reverse process possible ? That is, for a given norm n, how can we recover the inner product p such that n(x) =

\sqrt{p (x, x)}

Definitions 11.22 (Banach space, Hilbert space)

A vector space endowed with a norm which is a complete metric space is called Banach space.
A vector space endowed with an inner product which is a complete metric space is called Hilbert space.

Question 11.23

Which of the spaces described in Remark 11.12 are Banach ? Hilbert ?

12. Product spaces, quotient spaces

Definition 12.1 (product of two metric spaces)

Let (X,d_X) and (Y,d_Y) two metric spaces. Then the quantity d((x₁,y₁),(x₂,y₂)) defined by d((x₁,y₁),(x₂,y₂))² = d_X(x₁,x₂)² + d_Y(y₁,y₂)² is a distance on the set X×Y. We call product space to the metric space (X×Y,d)

Remark 12.2

One can define other distances on the set X×Y. For instance, d₁((x₁,y₁),(x₂,y₂)) = d_X(x₁,x₂) + d_Y(y₁,y₂) or d_∞((x₁,y₁),(x₂,y₂)) = max { d_X(x₁,x₂), d_Y(y₁,y₂) }. These metrics are equivalent to the one in definition 12.1 (which might have been denoted by d₂), so for studying topological properties of the product space any of these metrics can be used. See definition 9.54 and remark 12.5.

Remark 12.3

By repeatedly applying definition 12.1 we can define the product of any finite family of metric spaces.

Remark 12.4

The process described in remark 12.3 can be used to define the metric space ℝⁿ.

Remark 12.5

The convergence of a sequence (x_n,y_n) ∈ X × Y is equivalent to the convergence of x_n in X and of y_n in Y. A sequence (x_n,y_n) ∈ X × Y is Cauchy if and only if x_n is Cauchy in X and y_n is Cauchy in Y.

Remark 12.6

The product of two complete metric spaces is a complete metric space. To prove this, use the properties in remark 12.5.

Challenge 12.7

a) Describe the product between the real line ℝ and the circle S¹.
b) Describe the product between the circle S¹ and ( a copy of) itself.

Answers (difficulty level a:3, b:5)

a) This metric space could be called "cylinder". If we consider the Euclidean metric on S¹ (inherited from ℝ²), the product space is isometric to the usual cylindric surface { (x,y,z) ∈ ℝ³ : x²+y² = 1 }, with the Euclidean metric inherited from ℝ³. If we consider the geodesic metric on S¹, the product space is isometric to the "flat cylinder" in example 12.12.e.
b) This metric space could be called "torus". However, the details are tricky. If we consider the geodesic metric on (both copies of) S¹, the product space is isometric to the "flat torus" in example 12.12.f (rescaled by 2𝜋). Either with the geodesic distance or with the Euclidian distance on S¹, the product space is topologically equivalent but not isometric to the doughnut, also called torus of revolution.

Remark 12.8

Let (X,d_X) be a metric space and consider an equivalence relation ~ on X. We can define the quotient set Y = X/~ (definition 4.1), but is it possible to (naturally) define a distance on this quotient set ? Since each element of Y is a subset of X (an equivalence class), a reasonable definition would be to take the distance between subsets of X as distance on Y. However, there are many examples when this is not a distance on Y.

Remark 12.9

A specific equivalence relation can be defined on a metric space X by considering a group of isometries of X, that is, any subgroup 𝒢 of the group of all isometries (definition 7.15). The equivalence relation is then defined as : x~y ⇔ there exists an isometry φ ∈ 𝒢 such that y = φ(x). One can use the notation X/𝒢 instead of X/~.
Even in this case, it is not possible to prove, in general, that the distance between sets (equivalence classes) is a distance on the quotient set.
In certain particular cases, this can be proven, and we obtain the concept of quotient metric space.

Remark 12.10

Any translation φ : ℝⁿ → ℝⁿ can be expressed as φ(x) = x+v for a certain vector x ∈ ℝⁿ and thus φ can be identified with the vector v. Since the composition between translations corresponds to the sum of the vectors defining them, a group of translations can be identified with an additive subgroup of ℝⁿ.

Challenge 12.11 (quotient by a group of translations)

In the space ℝⁿ with the Euclidian metric, consider a group 𝒢 of translations, having m linearly independent generators, m ≤ n. Then the distance between equivalence classes is a distance on the quotient set ℝⁿ/𝒢.

Examples 12.12

a) If we take 𝒢 to be the trivial group (consisting of the identity only, which can be identified with the null vector) then ℝⁿ/𝒢 is isometric to ℝⁿ.
b) If we take, in ℝ, the group 𝒢 of translations given by integer numbers, then ℝ/𝒢 (which can be also denoted as ℝ/ℤ) is a metric space.
c) If we take, in ℝ, the group 𝒢 of translations given by multiples of 2𝜋, then ℝ/𝒢 is a metric space. It is isometric to S¹ with the geodesic distance.
d) If we take, in ℝ, the group 𝒢 of translations given by rational numbers, then ℝ/𝒢 (which can be also denoted as ℝ/ℚ) is not a metric space.
e) If we take, in ℝ², the group 𝒢 of translations given by pairs (2k𝜋,0) with k ∈ ℤ, then ℝ²/𝒢 is a metric space. We may call this metric space "flat cylinder". It is isometric to the product space in challenge 12.7.a (with the geodesic distance on S¹).
f) If we take, in ℝ², the group 𝒢 of translations given by pairs of integer numbers, then ℝ²/𝒢 (which can be also denoted as ℝ²/ℤ²) is a metric space. We may call this metric space "flat torus". If we slightly change the group 𝒢 by multiplying its elements by 2𝜋, we obtain a metric space which is isometric the product space in challenge 12.7.b (with the geodesic distance on both copies of S¹).
g) If we take, in ℝ², the group 𝒢 of translations generated by the two vectors (1,0) and (0.5,

\sqrt{0.75}

) (a hexagonal lattice) then ℝ²/𝒢 is a metric space which we may call "skew flat torus".

Challenge 12.13

Compute the diameter of the metric spaces in examples 12.13.bcfg.

Answers (difficulty level bc:3, f:4, g:5)

b) the diameter is 0.5
c) the diameter is 𝜋
f) the diameter is

\sqrt{0.5}

, or 𝜋

\sqrt{2}

, respectively
g) the diameter is

\sqrt{0.(3)}

Challenges 12.14 (finite groups of isometries)

On ℝ² with the Euclidian metric, consider the equivalence relations below. Each relation corresponds to a finite group 𝒢 of isometries; describe this group. Prove that the distance between subsets of ℝ² is a distance on ℝ²/𝒢. Describe this metric space.
a) (x₁,y₁) ~ (x₂,y₂) ⇔ x₁ = x₂, y₁ = -y₂
b) (x₁,y₁) ~ (x₂,y₂) ⇔ |x₁| = |x₂|, |y₁| = |y₂|
c) (x₁,y₁) ~ (x₂,y₂) ⇔ x₁ = -x₂, y₁ = -y₂
d) Generalize the example in c for a group generated by a rotation around the origin with angle 2𝜋/n.

Answers (difficulty level a:3, b:4, c:5, d:6)

a) 𝒢 has two elements, the identity and a symmetry with respect to the horizontal axis. ℝ²/𝒢 is isometric with the half-plane ℝ × [0,+∞[, with the Euclidian distance.
b) 𝒢 has four elements, the identity, two symmetries (with respect to each axis) and a rotation with 180º around the origin. ℝ²/𝒢 is isometric with the first quadrant [0,+∞[², with the Euclidian distance.
c) 𝒢 has two elements, the identity and a symmetry with respect to the horizontal axis. ℝ²/𝒢 is isometric with (half of) a cone C in ℝ², with the Euclidian distance. The cone is 60º wide. The equation defining the cone C is x² = 3y² + 3z²; if we add the inequation x ≥ 0, we obtain half of the cone.
d) 𝒢 has n elements, rotations around the origin. ℝ²/𝒢 is isometric with (half of) a cone C in ℝ². The angular opening of the cone is 2 arctan (1/n).

Challenge 12.15

On ℝ² with the Euclidian metric, consider the group of isometries 𝒢 consisting of all rotations around the origin.
Prove that the distance between subsets of ℝ² is a distance on ℝ²/𝒢.
Describe the quotient metric space ℝ²/𝒢.

Answer (difficulty level 4)

ℝ²/𝒢 is isometric with [0,+∞[.

Challenge 12.16

On the space S² = { (x,y,z) ∈ ℝ³ : x² + y² + z² = 1 }, with the geodesic distance, consider the group of isometries 𝒢 with two elements : the identity and the symmetry φ with respect to the origin, φ (x,y,z) = (-x,-y,-z).
Prove that the distance between subsets of S² is a distance on S²/𝒢.
Describe the quotient metric space S²/𝒢.

Answer (difficulty level 6)

S²/𝒢 is called projective plane. It is isometric with the metric space in question 6.9.c, because the angle between two straight lines passing through the origin is equal to the length of the arc joining the points where these lines intersect the sphere S².

Challenges 12.17

On X = ℝ × [-1,1] with the Euclidian metric, consider the equivalence relations ~ below. Prove that the distance between subsets of X is a distance on X/~. Describe this metric space.
a) (x₁,y₁) ~ (x₂,y₂) ⇔ y₂ = y₁ and x₂ = x₁ + 2k𝜋, k ∈ ℤ
b) (x₁,y₁) ~ (x₂,y₂) ⇔ (y₂ = y₁ and x₂ = x₁ + 2k𝜋, k ∈ ℤ) or (y₂ = -y₁ and x₂ = x₁ + 2k𝜋 + 𝜋, k ∈ ℤ) ⇔ y₂ = (-1)^ky₁ and x₂ = x₁ + k𝜋, k ∈ ℤ

Answers (difficulty level a:2, b:4)

a) This is the cartesian product between the space in challenge 12.12.c and [-1,1]. Thus, it is isometric to the piece of cylinder S¹ × [-1,1], with the geodesic metric on S¹.
b) This space is called Möbus strip.

Challenge 12.18

Compute the diameter of the metric spaces in examples 12.17.ab.

Answers (difficulty level a:2, b:5)

a) the diameter is

\sqrt{4 + 𝜋^{2}}

g) the diameter is

\frac{𝜋^{2} - 4}{2 𝜋}

Challenge 12.19

On [-1,1]² with the Euclidian metric, consider the equivalence relations ~ below. Prove that the distance between subsets of [-1,1]² is a distance on [-1,1]²/~. Describe this metric space.
a) (x₁,y₁) ~ (x₂,y₂) ⇔ ( x₁ = x₂, y₁ = y₂ ) or ( x₁ = x₂, y₁ = 1, y₂ = -1 ) or ( x₁ = x₂, y₁ = -1, y₂ = 1 ) or ( x₁ = 1, x₂ = -1, y₁ = y₂ ) or ( x₁ = -1, x₂ = 1, y₁ = y₂ )
b) (x₁,y₁) ~ (x₂,y₂) ⇔ ( x₁ = x₂, y₁ = y₂ ) or ( x₁ = x₂, y₁ = 1, y₂ = -1 ) or ( x₁ = x₂, y₁ = -1, y₂ = 1 ) or ( x₁ = 1, x₂ = -1, y₁ = -y₂ ) or ( x₁ = -1, x₂ = 1, y₁ = -y₂ )
c) (x₁,y₁) ~ (x₂,y₂) ⇔ ( x₁ = x₂, y₁ = y₂ ) or ( x₁ = -x₂, y₁ = 1, y₂ = -1 ) or ( x₁ = -x₂, y₁ = -1, y₂ = 1 ) or ( x₁ = 1, x₂ = -1, y₁ = -y₂ ) or ( x₁ = -1, x₂ = 1, y₁ = -y₂ )

Answers (difficulty level a:3, bc:6)

a) This is a flat torus. The only difference relatively to challenge 12.12.f is a zoom with ratio 2 (or 1/𝜋, respectively).
b) This is a possible definition of the Klein surface.
c) This space is topologically equivalent (but not isometric) to the projective plane described in question 6.9.c and challenge 12.16.

Topologic spaces

13. Definition, examples, base

Remark 13.1

We have seen in previous chapters that, in a metric space, the distance allows one to define the idea o proximity between points. Note that the idea of convergence of a sequence is tighlty related to the proximity between points : intuitively, a sequence of points is convergent if its terms get gradually closer and closer to a given point (the limit).
The main goal of topology is to describe the concept of proximity between points in a set without using a numerical quantity like the distance.

Remark 13.2

The concept of topology can be defined in several, equivalent ways.
a) We could make a (huge) list of convergent sequences, together with their respective limits. We should find out which properties of this selection lead us to a consistent theory. For instance, it makes sense to impose that a constant sequence converges to the respective constant. Also, it makes sense to assume that, if a certain sequence converges to a point x^⋆, any of its subsequences converges towards the same point x^⋆. Other assumptions may be necessary.
b) We could make a list of neighbourhoods of each point in the set. Again, we should impose certain properties of this list. For instance, a point should belong to each of its neighbourhoods. If V is a neighbourhood of a point x^⋆ and W is a set such that V ⊂ W then W should be a neighbourhood of x^⋆, too. Other properties are related to intersection of neighbourhoods.
Based on the notion of neighbourhood, we then define the concept of convergent sequence, of open set and so on.
c) We could make a list of sets to which we call "open sets". Again, we must choose a list of properties these sets should satisfy, for instance related to union and intersection.
Based on the notion of open set, we define the concept of convergent sequence, of closed set and so on. This is the approach followed by this textbook, see definition 13.3.
d) We could make a list of sets to which we call "closed sets". Again, we must choose a list of properties these sets should satisfy, for instance related to union and intersection.
Based on the notion of closed set, we define the concept of open set, of convergent sequence and so on.

Definition 13.3 (topology)

Let  X be a set. A topology on  X is a family 𝒯 of subsets of  X which we shall call "open sets". That is, 𝒯 ⊂ 𝒫(X). This family must satisfy the following properties
a) The empty set ∅ and the entire space X are open.
b) If 𝒜 is a family of open sets (that is, 𝒜 ⊂ 𝒯), possibly infinite, possibly not countable, then the union ⋃𝒜 is open (that is, ⋃𝒜 ∈ 𝒯).
c) If 𝒜 is a finite family of open sets (that is, 𝒜 ⊂ 𝒯), then the intersection ⋂𝒜 is open (that is, ⋂𝒜 ∈ 𝒯).
The pair (X,𝒯) is called topologic space.

Remark 13.4 (a distance defines a topology)

In a metric space, one defines the concept of open set (see definition 8.19) and these sets satisfy properties in definition 13.3 (see questions 8.28).

Example 13.5 (extreme topologies)

For a given set  X, the poorest topology is { ∅, X }. It is called indiscrete topology.
The richest topology is 𝒫(X). It is called discrete topology.

Remark 13.6 (finer and less fine topologies)

If 𝒯₁ and 𝒯₂ are two topologies on the same set  X such that 𝒯₁ ⊂ 𝒯₂, we say that 𝒯₁ is poorer, or less fine, or weaker, than 𝒯₂. We say that 𝒯₂ is richer, or finer, or stronger, or more separate, than 𝒯₁. We already used this terminology in example 13.5.

Remark 13.7

The topology induced by a discrete metric (see question 6.5.b) is precisely the discrete topology (see example 13.5).

Definition 13.8 (metrizable space)

Let (X,𝒯) be a topologic space. If there exists a distance on X which induces the topology 𝒯, we say that the space (X,𝒯) is metrizable.
Note that a distance defines uniquely a topology but not the other way around : there may exist different distances on X which induce the same topology; they are "called equivalent distances" (see definition 9.54).

Challenge 13.9

The discrete topology is metrizable (it can be defined based on the discrete distance).
The indiscrete topology is not metrizable.

Examples 13.10

a) On ℝ, the family of all semi-axes ]a,+∞[ satisfies properties 13.3.b and 13.3.c. Thus, if we add to this family two more elements, ∅ and ℝ, we get a topology.
b) What happens if we consider all semi-axes [a,+∞[ ?

Definition 13.11 (neighbourhood)

Let (X,𝒯) be a topologic space and let x^⋆ ∈ X. We say that a set V ⊂ X is a neighbourhood of x^⋆ if there is an open set A ⊂ X such that x^⋆ ∈ A ⊂ V.

Remark 13.12 (properties of neighbourhoods)

a) If V ⊂ X is a neighbourhood of x^⋆ and W is a set such that V ⊂ W then W is a neighbourhood of x^⋆, too.
b) If 𝒱 is a finite family of neighbourhoods of x^⋆ then their intersection ⋂𝒱 is also a neighbourhood of x^⋆.

Definition 13.13 (convergent sequence)

Let (X,𝒯) be a topologic space. Let x_n be a sequence in X and let x^⋆ ∈ X. We say that x_n converges to x^⋆ if for any neighbourhood V of x^⋆ there is an order N ∈ ℕ such that ∀ n ≥ N, x_n ∈ V.

Remarks 13.14

a) In a metric space, definition 13.13 reduces to definition 9.1; see remark 9.8
b) If a sequence converges, any of its subsequences converges, towards the same limit.

Challenge 13.15

Describe the convergent sequences in the discrete topology, in the indiscrete topology and in the topology in example 13.10.a.

Remark 13.16

A weaker topology has less open sets than a stronger one (see definition 13.6).
Consequently, in a weaker topology, each point has less neighbourhoods than in a stronger one.
Another consequence is that a weaker topology has more convergent sequences than a stronger one. In other words : strong convergence implies weak convergence.

Definition 13.17 (closed set)

In a topologic space (X,𝒯), a set F ⊂ X is called closed if its complementary X \ F is open.
Remarks 8.22, 9.26 and 9.31, stated for metric spaces, apply to the topologic context.

Definition 13.18 (sequentially closed set)

In a topologic space (X,𝒯), a set F ⊂ X is called sequentially closed if, for any sequence (x_n) ⊂ F which converges (in X) to some x^⋆ ∈ X, one has x^⋆ ∈ F.

Challenge 13.19 (a closed set is sequentially closed)

Prove that closedness implies sequential closedness.

Answer (difficulty level 3)

Consider a closed set F ⊂ X and a sequence x_n ∈ F converging to some x^⋆ ∈ X. Suppose x^⋆ does not belong to F; thus x^⋆ ∈ X\F. Since F is closed, X\F is open; so, by the definition of convergence, there is an order N ∈ ℕ such that x_n ∈ X\F for all n ≥ N which is a contradiction.

Remark 13.20

For metric spaces, we have followed a reverse approach : the concept of closed set was defined by means of convergent sequences (definition 9.21) and later we observed that this concept is equivalent to the complement being open (challenge 9.24).
Thus, in a metric space, closedness is equivalent to sequential closedness.

Challenge 13.21

Let (x_n) be a sequence in a topologic space X such that none of its subsequences converges (of course the sequence itself does not converge either). Then
a) None of the elements of the sequences shows up infintely many times in the sequence.
b) The set C = { x_n, n ∈ ℕ } ⊂ X is sequentially closed.
This will be useful in challenge 17.12.c.

Answer (difficulty level a:1, b:4)

If an element showed up infinitely many times, this would give rise to a constant (thus convergent) subsequence.
Suppose that C is not sequentially closed; thus, there is a sequence of elements of C which converges to some element not belonging to C. It is tedious but not very difficult to show that such a sequence is actually a subsequence of (x_n) and this contradicts the hypothesis.

Remark 13.22

We define the interior of a set A ⊂ X as the largest open set contained in A. Items 8.35 - 8.38, stated for metric spaces, apply to the topologic context.
We define the closure of a set A ⊂ X as the smallest closed set containing A. Items 9.38 - 9.40, stated for metric spaces, apply to the topologic context.
We define the concept of clopen set just like for metric spaces, see definition 9.37.
We define the boundary of a set just like for metric spaces, ∂A = A \ 

\overset{\circ}{A}

, see definition 9.49. Remark 9.50, stated for metric spaces, applies to the topologic context.
We define the concept of dense set just like for metric spaces, see definition 9.51. Question 9.53, stated for metric spaces, applies to the topologic context.
Properties involving the distance, like 8.39 or 9.42, do not apply to the topologic contex, obviously.

Questions 13.23

It is not easy to describe a topology because often there are many open sets, and they may have a complicated structure. It would be nice if we could just list some of the open sets and then let the properties in definition 13.3 "do the job" of describing the rest of the family of open sets.
More precisely, given a family 𝒜 of sets which we intend to call "open" but which do not verify properties in definition 13.3, we question : is there a topology containing 𝒜 ? The answer is obvius, since 𝒫(X) is a topology which surely contains 𝒜. We now refine the question : which is the smallest, or poorest, topology  𝒯 containing 𝒜 ?
Actually, the correct approach is to first question the very existence of such a topology. See remark 13.24 and challenge 13.25.

Remark 13.24 (explicit construction of a topology from a set of open sets)

Taking into account the type of properties we want this family of sets to fulfill (definition 13.3) our intuition suggests a constructive process, consisting of successivly enlarging the family 𝒜. We first add ∅ and  X to the family. Then we add all possible unions of sets in the family. Then we add all possible finite intersections of sets in the family. Is this a topology ? Not yet; by construction, it satisfies properties 13.3.a and 13.3.c but not necessarily 13.3.b. Well, let us add, again, all possible unions of sets in the family. Is this a topology ? By construction, it satisfies properties 13.3.a and 13.3.b but not necessarily 13.3.c.
This process may never end.

Challenge 13.25

Rather than enlarging successively the family 𝒜, we may try a reverse approach : start with the largest topology 𝒫(X) and then search for smaller (poorer) topologies still containing 𝒜.
Let 𝒜 be a family of subsets of  X. Consider the family of all topologies containing 𝒜. This is an ordered set, with the inclusion between topologies. Prove that it has a minimum element.
This minimum element is called topology generated by 𝒜.

Answer

It is not difficult to prove that the intersection of arbitrarily many topologies is a topology. Then the minimum element can be defined as the intersection of all topologies on X which contain 𝒜.

Remark 13.26

The concept of topology generated by a family of sets can be useful for certain theoretical constructs and properties. Here is an example.
Let 𝒯₁ and 𝒯₂ be two topologies on a set  X. Suppose we would like to prove that 𝒯₁ ⊂ 𝒯₂, i.e. that 𝒯₁ is weaker than 𝒯₂. If 𝒯₁ is generated by a family 𝒜 ⊂ 𝒯₁ then it is enough to prove that 𝒜 ⊂ 𝒯₂; this implies immediately that 𝒯₁ ⊂ 𝒯₂. Why ?

Answer

Because, by definition, 𝒯₁ is the smallest (weakest) topology containing 𝒜, thus it must be weaker than 𝒯₂.

Remark 13.27

We can weaken the construction in remark 13.26 as follows.
Consider two families 𝒜₁ and 𝒜₂ of subsets of  X. Suppose 𝒜₁ generates a topology 𝒯₁ and 𝒜₂ generates a topology 𝒯₂. If any element of 𝒜₁ can be written as a union of elements of 𝒜₂ then 𝒯₁ ⊂ 𝒯₂.

Remark 13.28

Let 𝒜 be a family of subsets of  X. Let C ⊂ X be a set. Saying that C can be written as a union of elements of 𝒜 is equivalent to saying that ∀ x ∈ C, ∃ A ∈ 𝒜 such that x ∈ A ⊂ C.

Remark 13.29

The "top-to-bottom" process described in challenge 13.25 is not explicit enough, thus is not convenient.
There are situations where a constructive approach similar to the one in remark 13.24 works; see challenge 13.30.

Challenge 13.30

Let 𝒜 be a family of subsets of  X such that the intersection between any two sets in 𝒜 can be written as a union of a family (possibly infinte, possibly uncountable) of sets in 𝒜. Assume also that the union of all elements in 𝒜 is  X (in other words, 𝒜 is a covering of  X). Then the family 𝒯 of all unions of subfamilies (possibly infinite, possibly uncountable) of 𝒜 is a topology. Prove.
A family 𝒜 with the above property is called a topologic basis.
We may also say that 𝒜 is a basis of the topology 𝒯.

Remark 13.31

Due to the equivalence in remark 13.28, we have that 𝒜 ⊂ 𝒫(X) is a basis of a certain topology 𝒯 if ∀ D ∈ 𝒯, ∀ x ∈ D, ∃ A ∈ 𝒜 such that x ∈ A ⊂ D.

Examples 13.32

a) The family of all open intervals ]a,b[ ⊂ ℝ, with a,b ∈ ℝ, is a basis of the Euclidian topology on ℝ.
b) The family of all open intervals ]p,q[ ⊂ ℝ, with p,q ∈ ℚ, is a basis of the Euclidian topology on ℝ.
c) Describe the topology on ℝ generated by the family of all closed intervals [a,b] ⊂ ℝ, with a,b ∈ ℝ.
d) Is the family in example c above a topologic basis ?
e) Describe the topology on ℝ generated by the family of all semi-closed intervals [a,b[ ⊂ ℝ, with a,b ∈ ℝ.
f) Is the family in example e above a topologic basis ?
g) The family of all open balls in ℝ² is a basis of the Euclidian topology on ℝ².
h) The family of open balls in ℝ² whose center has rational coordinates and of rational radius is a basis of the Euclidian topology on ℝ².
i) The family of all open rectangles in ℝ² is a basis of the Euclidian topology on ℝ².
j) The family of all open rectangles in ℝ² with sides parallel to the axes is a basis of the Euclidian topology on ℝ².
k) The family of all open rectangles in ℝ² with sides parallel to the axes and with rational sidelengths is a basis of the Euclidian topology on ℝ².
l) The family of all open triangles in ℝ² is a basis of the Euclidian topology on ℝ².
m) The family of all open equilateral triangles in ℝ² is a basis of the Euclidian topology on ℝ².

Remark 13.33

In example 13.32.l above, we should not be mistaken by the following construct.
We want to prove that the intersection of any two triangles can be written as union of triangles. One of the cases we must take into consideration is depicted in the figure below. So, we must prove that an open hexagon is a union of open triangles. At first view, one may think that any hexagon is the union of four triangles, depicted also in the figure below. However, in the present context this would be a mistake since we are talking about open triangles. Thus, the union of the four open triangles in the figure is not equal to the open hexagon; three segments are missing.
two intersecting triangles

Definition 13.34 (separate space, Hausdorff space)

We say that a topologic space (X,𝒯) is T2, or separate, or Hausdorff, if any two distinct points have disjoint neighbourhoods.

Question 13.35

Among the topologic spaces introduced in this textbook, which are Hausdorff ?

Remark 13.36

A metric space is Hausdorff (see challenge 8.31).
A metrizable topologic space is Hausdorff.

Remark 13.37

In a Hausdorff space, the limit of a convergent sequence is unique.

Definition 13.38 (fundamental system of neighbourhoods)

Let (X,𝒯) be a topologic space and let x^⋆ ∈ X. We call a base of neighbourhoods at x^⋆ (or fundamental system of neighbourhoods) to a family 𝒱_x^⋆ of neighbourhoods of x^⋆ such that for any neighbourhood V of x^⋆ there is a W ∈ 𝒱_x^⋆ such that W ⊂ V.

Examples 13.39

a) In any topologic space (X,𝒯), the family of all open neighbourhoods of a point is a fundamental system of neighbourhoods.
b) In a metric space (X,d), the family of all open balls centered at x^⋆ is a fundamental system of neighbourhoods of x^⋆.
c) In a metric space (X,d), the family of open balls centered at x^⋆ having rational radius is a fundamental system of neighbourhoods of x^⋆.
d) In a metric space (X,d), the family of all closed balls centered at x^⋆ is a fundamental system of neighbourhoods of x^⋆.
e) In a metric space (X,d), the family of closed balls centered at x^⋆ having rational radius is a fundamental system of neighbourhoods of x^⋆.
f) In ℝ², the family of all open equilateral triangles centered at x^⋆ is a fundamental system of neighbourhoods of x^⋆.
g) In a discrete topologic space, the family with one set only 𝒱_x^⋆ = { { x^⋆ } } is a fundamental system of neighbourhoods of x^⋆.

Definition 13.40 (first countable space)

We say that a topologic space (X,𝒯) is first countable if at any point of X there is a countable fundamental system of neighbourhoods.

Challenge 13.41

Let 𝒱 be a countable base of neighbourhoods of x^⋆. Since it is countable, we can organize it as a sequence 𝒱 = { V_n }. Moreover, we can build from it another base of neighbourhoods of x^⋆, organized as a decreasing sequence; it suffices to define W_n = V₁ ∩ V₂ ∩ ... ∩ V_n. Prove that { W_n } is indeed a fundamental system of neighbourhoods of x^⋆.

Answer (difficulty level 1)

Let W be any neighbourhood of x^⋆; since { V_n } is a fundamental system of neighbourhoods, there is some n ∈ ℕ such that V_n ⊂ W. But W_n ⊂ V_n so W_n ⊂ W, thus { W_n } is indeed a fundamental system of neighbourhoods of x^⋆.

Remark 13.42

Any metric space is first countable; see example 13.39.c or 13.39.e.
Any metrizable topologic space is first countable.

Challenge 13.43

Let 𝒱 be a countable base of neighbourhoods of x^⋆, organized as a decreasing sequence 𝒱 = { V_n } (see challenge 13.41 above). Let us choose, for each n ∈ ℕ, an arbitrary point x_n ∈ V_n. Then the sequence (x_n) thus constructed converges to x^⋆.

Answer (difficulty level 2)

Let W be any neighbourhood of x^⋆; since { V_n } is a fundamental system of neighbourhoods, there is some N ∈ ℕ such that V_N ⊂ W. Consequently, for all n ≥ N, x_n ∈ W and this proves that x_n converges to x^⋆.

Remark 13.44

In a first countable topologic space, sequential closedness implies closedness (thus, they are equivalent). See items 13.17 - 13.20.

Answer (difficulty level 6)

Consider a sequentially closed set F ⊂ X and suppose F is not closed. This means X\F is not open, so there is a point x^⋆ ∈ X\F which is not interior to X\F. Thus, there is no neighbourhood of x^⋆ disjoint of F. Let { V_n } be a fundamental system of neighbourhoods of x^⋆, ordered as a sequence. None of them is disjoint of F so let us choose, for each n ∈ ℕ, a point x_n ∈ V_n ∩ F. The sequence (x_n) thus constructed converges to x^⋆ (challenge 13.43). Since F is sequentially closed, this implies x^⋆ ∈ F which contradicts the assumption x^⋆ ∈ X\F.

Definition 13.45 (second countable)

We say that a topologic space (X,𝒯) is second countable if 𝒯 has a topologic base which is countable.

Remarks 13.46

a) Not any metric space is second countable.
b) ℝ² with the Euclidian topology is second countable; see example 13.32.h.
c) Any second countable topologic space is first countable.

14. Continuous functions, homeomorphisms

Remark 14.1

For a scalar function of one variable f : ℝ → ℝ, the usual definition of continuity (at a point x^⋆ ∈ ℝ) is lim_{x → x^⋆} f(x) = f(x^⋆). The same definition applies to a function of several variables, or to a vector function.
It is a nice exercise to prove that a function is continuous in all points of its domain if and only if, for any B ⊂ ℝ open, the inverse image f^-1(B) is also open.
Actually, these two properties are equivalent even for a function between two metric spaces (challenge 14.6).
For the more general context of a function between two topologic spaces f : (X,𝒯_X) → (Y,𝒯_Y), these two properties are no longer equivalent. Thus, we shall use different names for them; the former will be called "sequential continuity" (see definition 14.4) while the latter will be called "continuity" (see definition 14.2).

Definition 14.2 (continuous function)

A function f : (X,𝒯_X) → (Y,𝒯_Y) is said to be continuous on X if, for any open set B ⊂ Y (that is, B ∈ 𝒯_Y), the inverse image f^-1(B) is open in X (that is, f^-1(B) ∈ 𝒯_X).

Remark 14.3

Since a closed set is simply the complementary of an open set, definition 14.2 can be reformulated as "inverse images of closed sets are closed".

Definition 14.4 (sequentially continuous function)

A function f : (X,𝒯_X) → (Y,𝒯_Y) is said to be sequentially continuous on X if, for any convergent sequence in X x_n → x^⋆, the sequence of images (values of f) also converges in Y towards the corresponding value of f : f(x_n) → f(x^⋆).

Challenge 14.5

Prove that continuity (definition 14.2) implies sequential continuity (definition 14.4).

Challenge 14.6

Prove that, in a metric space, continuity (definition 14.2) is equivalent to sequential continuity (definition 14.4).

Questions 14.7

a) Does a continuous function (forward) transport open sets into open sets ?
b) Does a continuous function (forward) transport closed sets into closed sets ?

Questions 14.8

Let (X,𝒯_X) be a topologic space and let Y be a set. Let f : X → Y be a function.
a) Is there a topology on Y which turns f continous ? The answer is easy; if there are few open sets in Y the continuity is ensured (see definition 14.2) so we choose the indiscrete topology { ∅, Y }.
b) Are there richer topologies on Y such that f is still continuous ? The answer depends on the example at hand; there may be.
c) Is there a "richest" topology on Y among those which preserve f continous ?
d) Is there an explicit, constructive, definition of the richest topology ?

Answer

c) First, let us stress that an argument similar to the one in challenge 13.25 does not work here. If we consider the family of all topologies on  Y which make f continuous, ordered with the inclusion, there is no reason for a maximum element to exist a priori. The union of such a family of topologies may not be a topology.
The answer is positive, though, due to the constructive proof in item d below.
d) Let us first show a failed tentative. One could try to define the family { f(A) : A ∈ 𝒯_X }. However, this is not a topology in general.
Inverse images have "nicer" properties than forward images of sets. The "richest" topology on  Y which makes f continuous can be defined as { B ⊂ Y : f^-1(B) ∈ 𝒯_X }. It is easy to prove that this is a topology on  Y and that it makes f continuous.

Definition 14.9 (forward image of a topology)

Let (X,𝒯_X) be a topologic space and let Y be a set. Let  f : X → Y be a function. We call forward image of  𝒯_X  through  f  to the richest topology on  Y  which keeps  f  continuous (see questions 14.8).

Questions 14.10

Let (Y,𝒯_Y) be a topologic space and let X be a set. Let f : X → Y be a function.
a) Is there a topology on X which turns  f  continous ? The answer is easy; if there are many open sets in X the continuity is ensured (see definition 14.2) so we choose the discrete topology 𝒫(X).
b) Are there poorer topologies on  X such that  f  is still continuous ? The answer depends on the example at hand; there may be.
c) Is there a "poorest" topology on  X among those which preserve  f  continuous ?
d) Is there an explicit, constructive, definition of the poorest topology ?

Answer

c) Yes, due to an argument similar to the one in challenge 13.25. The intersection of a family of topologies which make f continuous is a topology which makes f continuous. Or, see the constructive proof in item d below.
d) The "poorest" topology on  X among those which preserve  f  continuous can be defined as { f^-1(B) : B ∈ 𝒯_Y }. It is easy to prove that this is a topology on  X and that it makes f continuous.

Definition 14.11 (inverse image of a topology)

Let (Y,𝒯_Y) be a topologic space and let X be a set. Let f : X → Y be a function. We call inverse image of  𝒯_Y  through  f  to the poorest topology on  X which keeps  f  continuous (see questions 14.10).

Definition 14.12 (topologic subspace)

Let (X,𝒯) be a topologic space and let C ⊂ X be a subset. Consider i : C → X be the inclusion application; the inverse image of 𝒯 through i is a topology on C called the induced topology. The set C, endowed with this topology, is called a topologic subspace of X.
It is easy to see that a set A ⊂ C is open in the induced topology if and only if there exists an set B ⊂ X, open in the topology 𝒯, such that A = B ∩ C.

Remark 14.13

Let (X,𝒯_X) and (Y,𝒯_Y) be two topologic spaces and let f : X → Y be a function. It is not difficult to see that the following assertions are equivalent.
a)  f  is continuous
b) The forward image of 𝒯_X through  f  is richer than (includes) 𝒯_Y.
c) The inverse image of 𝒯_Y through  f  is poorer than (is included in) 𝒯_X.

Definition 14.14 (homeomorphism)

A bijection f : (X,𝒯_X) → (Y,𝒯_Y) which is continuous and whose inverse f^-1 is also continuous is called a homeomorphism between the spaces (X,𝒯_X) and (Y,𝒯_Y).

Remark 14.15

Since a homeomorphism transforms open sets into open sets (and thus closed sets into closed sets) both ways, that is, from X to Y and also from Y to X, all topologic properties of X are transferred to Y. In particular, if X is connected so is Y (see section 16), if X is compact so is Y (see section 17). From the topologic viewpoint, spaces (X,𝒯_X) and (Y,𝒯_Y) are indistinguishable.

Remark 14.16

Topology can be defined as "the study of properties which are invariant upon homeomorphisms"; see remark 14.15.

Challenge 14.17

Any isometry is a homeomorphism.
Not every homeomorphism is an isometry. A homeomorphism can deform distances (if a distance is defined at all).

Questions 14.18

Are these two topologic spaces homeomorphic ? That is, is there a homemorphism between them ?
a) ]0,1[ and ℝ
b) [0,1[ and [0,+∞[
c) ]0,1[ and [0,+∞[
d) ℝ and ℝ²

Challenge 14.19

Let (X,𝒯_X) and (Y,𝒯_Y) be two topologic spaces. Let f : X → Y be a bijection such that ∀ x^⋆ ∈ X, there is a neighbourhood V ⊂ X of x^⋆ such that W = f(V) is a neighbourhood of f(x^⋆) and f is a homeomorphism between V and W. Prove that f is a homemorphism between X and Y.
In other words : a bijection which is a local homeomorphism is a homeomorphism.

Remark 14.20

As a consequence of challenge 14.19, any local isometry (definition 7.18) is a homeomorphism.
This implies that the two metric spaces in question 7.21.c are homeomorphic.

15. Product spaces, quotient spaces

Definition 15.1 (inverse image of a family of topologies)

Let (Y_i,𝒯_i) be a family of topologic spaces (possibly infinite, possibly uncountable) and let X be a set. Let f_i : X → Y_i be a family of functions. We call inverse image of the topologies 𝒯_i through f_i to the poorest topology on X which makes all functions f_i continuous.

Remark 15.2

Definition 15.1 is a generalization of definition 14.12 and the existence of the inverse image can be proven as in question 14.10.c. The intersection of a family of topologies which make all f_i continuous is a topology which makes all f_i continuous.
However, the explicit construction shown in question 14.10.d is no longer valid; see remark 15.3.

Remark 15.3

Consider, for each i fixed, the inverse image of 𝒯_i through f_i, denoted by f_i^-1(𝒯_i). Each f_i^-1(𝒯_i) is a topology on X. However, their union ⋃_i f_i^-1(𝒯_i) is not a topology, not even a topologic base.
The inverse image described in definition 15.1 can be defined as the topology generated by the above union.

Definition 15.4 (product topology)

Let (Y_i,𝒯_i) be a family of topologic spaces (possibly infinite, possibly uncountable) and let X = ∏_iY_i be their cartesian product. Let 𝜋_i : X → Y_i be the canonical projection on Y_i. The inverse image of the topologies 𝒯_i through 𝜋_i, in the sense of definition 15.1, is called the product topology on ∏_iY_i.

Remark 15.5

Consider the cartesian product of two sets Y₁×Y₂. If B₁ is a subset of Y₁ then 𝜋₁^-1(B₁) = B₁×Y₂; this can be interpreted as a "vertical strip". If B₂ is a subset of Y₂ then 𝜋₂^-1(B₂) = Y₁×B₂; this can be interpreted as a "horizontal strip". Their intersection 𝜋₁^-1(B₁) ∩ 𝜋₂^-1(B₂) is simply the "rectangle" B₁ × B₂.
Consider the cartesian product of three sets Y₁×Y₂×Y₃. If B₁ is a subset of Y₁ then 𝜋₁^-1(B₁) = B₁×Y₂×Y₃. If B₂ is a subset of Y₂ then 𝜋₂^-1(B₃) = Y₁×B₂×Y₃. If B₃ is a subset of Y₃ then 𝜋₃^-1(B₃) = Y₁×Y₂×B₃. These sets can be interpreted as "layers". Their intersection 𝜋₁^-1(B₁) ∩ 𝜋₂^-1(B₂) ∩ 𝜋₃^-1(B₃) is simply the "parallelipiped" B₁×B₂×B₃.
Similar considerations are valid for the cartesian product of an arbitrary family of sets Y_i.

Remark 15.6

If X is the product of a finite family of topologic spaces, the product of open sets can be viewed as the (finite) intersection of "layers"; see remark 15.5. Since each "layer" is open in X by definition and the intersection of a finite family of open sets is still open, we conclude that the product of open sets (which can be viewed as a "parallelipiped") is open.
We know that the family of all "layers" generates the product topology; see remark 15.3. It is not difficult to check that the above "open parallelipipeds" form a base for the product topology.

Remark 15.7

If X is the product of an infinite family of topologic spaces, the product of open sets can still be viewed as an intersection of "layers" (see remark 15.5) but this time we are talking of an infinite family of "layers". There is no reason for such an intersection to be open in X.

Remark 15.8

If X is the product of an infinite family of topologic spaces, the family of all "layers" generates the product topology; see remark 15.3.
It is not difficult to prove that the family of all finite intersections of "layers" is a basis for the product topology. Such a finite intersection of "layers" is equal to the direct product ∏_iB_i where each B_i is an open set in Y_i and B_i = Y_i for all i with the exception of a finite number of indices.

Questions 15.9

a) In a product of topologic spaces, is the projection of an open set open ?
b) In a product of topologic spaces, is the projection of a closed set closed ?

16. Connected spaces

Definition 16.1 (connected space)

A topologic space (X,𝒯) is said to be disconnected if there is a (non-trivial) partition of X with open sets.
In other words, a topologic space (X,𝒯) is disconnected if there exists a subset A ⊂ X which is open and whose complementary X\A is also open.
In other words, a topologic space (X,𝒯) is disconnected if there exists a (non-trivial) clopen set, a set which is simultaneously closed and open.
In other words, a topologic space (X,𝒯) is disconnected if there are two non-empty subsets A and B such that A∪B = X, A ∩ B = ∅ and A ∩ B = ∅.
A topologic space is said to be connected if it is not disconnected.

Question 16.2

In a disconnected space, must there exist two non-empty subsets A and B such that A∪B = X and A ∩ B = ∅ ?

Challenge 16.3

Prove that ℝ (with the Euclidian topology) is connected.

Definition 16.4 (connected set)

Let (X,𝒯) be a topologic space; a subset C ⊂ X is said to be connected if C, with the topology induced from X (definition 14.12), is a connected topologic space.

Remark 16.5

Unlike other properties (see remarks 8.22 and 9.31), connectedness of a set does not describe the relation between that set and the surrounding space; we may say it is an intrinsic property.
More precisely : if a set C is included in two different topologic spaces X and Y, as long as the induced topology on C is the same, then C is connected as a subset of X if and only if it is connected as a subset of Y.

Challenge 16.6

Let (X,𝒯) be a topologic space and C ⊂ X a disconnected subset. Does this imply that there are two non-empty A and B such that A∪B = C and A ∩ B = ∅ ? Note that the closure is relative to the space X.

Challenge 16.7

Let (X,𝒯) be a topologic space and let C ⊂ X be a connected subset. Consider D ⊂ X another subset such that C ⊂ D ⊂ C. Prove that D is connected.
In particular, the closure of a connected set is connected.
Is the interior of a connected set connected ?

Challenge 16.8

Let (X,𝒯) be a topologic space and let C_i ⊂ X be a family of connected sets with non-empty intersection : ⋂_iC_i ≠ ∅. Then their union ⋃_iC_i is connected.

Challenge 16.9

Prove that ℝⁿ (with the Euclidian topology) is connected.

Answer

Recall that a straight line in ℝⁿ is connected (since it is homeomorphic to ℝ). It suffices to note that ℝⁿ is the union of all straight lines passing through the origin and apply challenge 16.8.

Challenge 16.10

A continuous function transforms connected sets in connected sets.

Definition 16.11 (path)

Let (X,𝒯) be a topologic space and let a and b be two points in X. We call path from a to b to any continuous function γ : [0,1] → X such that γ(0) = a and γ(1) = b.
This is a weaker notion than the one introduced in remark 6.31; here we only impose continuity of γ.

Definition 16.12 (space connected by paths)

A topologic space (X,𝒯) is said to be connected by paths if for any two points a, b ∈ X there is a path in X from a to b.

Challenge 16.13

A space connected by paths is connected.
Is the reverse true ?

Challenge 16.14

A continuous function transforms sets connected by paths in sets connected by paths.

Definition 16.15 (connected component)

Let (X,𝒯) be a topologic space and let x^⋆ ∈ X be a point. Consider the family of all connected subsets of X containing x^⋆. Does it have a maximum element (with the order relation given by the inclusion) ?
The answer would be difficult if not for the property in challenge 16.8 : the union of all these sets is itself a connected set and thus it is a maximum element. It is called connected component associated to x^⋆.

Remark 16.16

Let (X,𝒯) be a topologic space; the family of all connected components in X is a partition of X. Each element of this partition is a clopen set (definition 16.1).

Challenge 16.17

In a normed space, a convex set is connected.

Challenge 16.18

In a normed space, a star-shaped set is connected.

17. Compact spaces

Remark 17.1

We learn in real analysis to call "compact" any closed bounded set K ⊂ ℝⁿ.
We can talk about closed bounded sets in any metric space. However, these sets do not necessarily satisfy other properties that we usually expect from compact sets, like the ones in definitions 17.2 or 17.4. See e.g. challenge 17.19.e.
In a topologic context, there are no bounded or unbounded sets since there is no distance to measure diameteres.

Definition 17.2 (sequential compactness)

A topologic space (X,𝒯) is said to be sequentially compact if any sequence in X has a convergent subsequence.

Challenge 17.3

Prove that
a) ℝ, with the Euclidian topology, is not sequentially compact.
b) ]0,1], with the Euclidian topology, is not sequentially compact.
c) [0,1], with the Euclidian topology, is sequentially compact.
d) On any set X, the indiscrete topology { ∅,X } is sequentially compact.

Definition 17.4 (compactness)

A topologic space (X,𝒯) is said to be compact if any covering 𝒜 of X with open sets has a finite subcovering. See definitions 1.42 and 1.46.

Remark 17.5

Some authors include in the definition of compactness the property of the space being Hausdorff (definition 13.34).

Remark 17.6

One can re-write definition 17.4 in terms of complementary sets. A topologic space (X,𝒯) is said to be compact if, for any family ℱ of closed sets whose intersection is empty, there exists a finite subfamily ℱ^⋆ ⊂ ℱ whose intersection is still empty.

Challenges 17.7

Prove that
a) ℝ, with the Euclidian topology, is not compact.
b) ]0,1], with the Euclidian topology, is not compact.
c) [0,1], with the Euclidian topology, is compact.
d) On any set X, the indiscrete topology { ∅,X } is compact.

Answer

c) This is difficult to prove directly. It is easier to prove that [0,1] is countably compact, see challenge 17.11.c.

Definition 17.8 (countable compactness)

A notion slightly weaker than compactness is : any countable covering 𝒜 of X with open sets has a finite subcovering. We call this property countable compactness.

Challenge 17.9

Prove that the property stated below is equivalent to countable compactness.
For any increasing sequence of open sets B₁ ⊂ B₂ ⊂ B₃ ⊂ ... whose union is X, there is an N ∈ ℕ such that B_N = X.

Answer (difficulty level 4)

Assume X is countably compact and consider an increasing sequence of open sets B₁ ⊂ B₂ ⊂ B₃ ⊂ ... whose union is X. According to definition 17.8, there is a finite subcovering B_n₁, B_n₂, ... B_{n_m}. Since the sets B_n increase with n, B_n₁ ∪ B_n₂ ∪ ...  ∪ B_{n_m} = B_{n_m} = X.
Conversely, assume X satisfies the property stated in the challenge and consider a countable covering 𝒜 = { A₁, A₂,A₃,... } of X (not necessarily increasing). We want to prove that there is a finite subcovering of 𝒜. For each n ∈ ℕ, define B_n = A₁ ∪ A₂ ∪ ... ∪ A_n. We thus obtain an increasing sequence of open sets B₁ ⊂ B₂ ⊂ B₃ ⊂ ... Since each B_n contains A_n, the union of all B_n contains the union of all A_n which is X. Applying the property stated in the challenge, there is an N ∈ ℕ such that B_N = X which implies A₁ ∪ A₂ ∪ ... ∪ A_N = X so this is a finite subcovering of 𝒜.

Remark 17.10

In the spirit of remark 17.6, one can re-write the property stated in challenge 17.9 above as :
For any decreasing sequence of closed sets F₁ ⊃ F₂ ⊃ F₃ ⊃ ... whose intersection is ∅, there is an N ∈ ℕ such that F_N = ∅.
Still another way of putting it is : any decreasing sequence of non-empty closed sets has non-empty intersection.

Challenges 17.11

Prove that
a) ℝ, with the Euclidian topology, is not countably compact.
b) ]0,1], with the Euclidian topology, is not countably compact.
c) [0,1], with the Euclidian topology, is countably compact.

Challenges 17.12

a) Prove that a compact space is countably compact.
b) Prove that a sequentially compact space is countably compact.
c) Prove that a first countable space which is countably compact is sequentially compact.

Answers (difficulty level a:1, b:5, c:7)

a) The proof is really simple.
b) Let X be a sequentially compact topologic space. In the spirit of remark 17.10, consider a decreasing sequence of non-empty closed sets F₁ ⊃ F₂ ⊃ ... For each n, choose a point x_n ∈ F_n; we thus obtain a sequence (x_n) in X; by hypothesis, this sequence has a convergent subsequence x_{n_k} → x^⋆ ∈ X. For each fixed m ∈ ℕ, the points x_{n_k} belong, starting from a certain order, to the set F_m which is closed. Thus, for each fixed m ∈ ℕ, x^⋆ ∈ F_m. So, x^⋆ belongs to the intersection of all F_m, so this intersection is not empty. This proves that X is countably compact.
c) Let X be a first countable topologic space which is countably compact. Due to remark 13.44, in such a space closedness is equivalent to sequential closedness. Let (x_n) be a sequence of points in X; we want to prove that (x_n) has a convergent subsequence. Supposing (x_n) has no convergent subsequence, challenge 13.21.b implies that the set F_m = { x_n, n ≥ m } is sequentially closed (and thus closed). We have built a decreasing sequence of non-empty closed sets F_m. Since by hypothesis X is countably compact, the intersection of all sets F_m is non-empty (see remark 17.10). This contradicts challenge 13.21.a.

Challenge 17.13

Prove that, for a second countable topologic space, countable compactness implies compactness. Together with challenge 17.12.a, this implies that (in a second countable space) countable compactness is equivalent to compactness.

Answer (difficulty level 5)

Let (X,𝒯) be a second countable topologic space; let B₁,B₂,B₃,... be a countable topologic base in X. Suppose X is countably compact. Let 𝒜 = (A_α)_α∈I be a covering of X with open sets (I not necessarily countable). Each A_α can be written as a union of elements in the topologic base, A_α = ⋃_{n∈N_α} B_n, where N_α is a subset of ℕ. Then the family (B_n)_{n∈N_α,α∈I} is also a covering (with open sets) of X. The family (B_n)_{n∈N_α,α∈I} is countable since it is included in the base B₁,B₂,B₃,.... (This may seem contradictory, as (B_n)_{n∈N_α,α∈I} seems larger than 𝒜. The apparent contradiction is explained by the fact that many of the sets B_n are repeated.) Since by hypothesis X is countably compact, (B_n)_{n∈N_α,α∈I} has a finite subcovering B_n₁,B_n₂,...,B_{n_m} with each n_k belonging to some N_{α_k}. This implies that A_α₁,,A_α₂,...,A_{α_m} is a finite subcovering of 𝒜 and this concludes the proof.

Challenge 17.14

Prove that, for a metric space, compactness is equivalent to sequential compactness and to countable compactness.
The proof can be perfomed following the chain of implications below.
a) For a metric space, sequential compactness is equivalent to countable compactness.
b) For a metric space, compactness implies countable compactness.
c) For a metric space, sequential compactness implies compactness.

Answers (difficulty level a:2, b:1, c:9)

a) Since a metric space is first countable (remark 13.42), it suffices to apply challenges 17.12.bc.
b) Apply challenge 17.12.a.
c) Let (X,d) be a sequentially compact metric space. It suffices to prove that X is second countable; then the assertion will follow from challenge 17.13. The proof that X is second countable is difficult; see here.

Challenge 17.15

Prove that a compact metric space is bounded.

Answer (difficulty level 3)

Let (X,d) be a compact metric space (thus, countably compact). Choose and fix a point x^⋆ ∈ X. For each n ∈ ℕ, consider the open ball B (x^⋆,n) of center x^⋆ and radius n. This is an increasing sequence of open sets covering X. According to challenge 17.9, there is an N ∈ ℕ such that B (x^⋆,N) = X which means X is bounded.

Challenge 17.16

Prove that a compact metric space is complete.

Answer (difficulty level 2)

Let (X,d) be a compact metric space (thus, sequentially compact). Consider a Cauchy sequence (x_n) ⊂ X; since X is sequentially compact, (x_n) has a convergent subsquence. According to challenge 10.13, (x_n) converges and this proves that X is complete.

Remark 17.17 (compact sets)

Notions like compactness, sequential compactness and countable compactness extend naturally from spaces to subsets. That is, a subset K of a topologic space X is said to be compact (or sequentially compact, or countably compact) if it is compact (or sequentially compact, or countably compact) as a subspace of X.
This terminology has been implicitly used in challenges 17.7.bc and 17.11.bc.

Remark 17.18

Unlike other properties (see remarks 8.22 and 9.31), compactness of a set does not describe the relation between that set and the surrounding space; we may say it is an intrinsic property.
More precisely : if a set K is included in two different topologic spaces X and Y, as long as the induced topology on K is the same, then K is compact as a subset of X if and only if it is compact as a subset of Y.

Challenges 17.19

a) Prove that a closed subset of a compact space is compact.
b) Prove that a closed subset of a countably compact space is a countably compact.
c) Prove that a closed subset of a sequentially compact space is sequentially compact.
d) Let (X,d) be a metric space and K be a compact subset of X. Prove that K is closed in X.
e) Show an example of a closed bounded subset of a metric space which is not compact.

Challenge 17.20

Prove that a continuous function transforms compact spaces/sets in compact spaces/sets.

Challenge 17.21

Prove that a sequentially continuous function transforms sequentially compact spaces/sets in sequentially compact spaces/sets.

Index

bounded : 6.27
Cauchy sequence : 10.1
closed set : 9.21, 13.17
clopen set : 9.37
closure : 9.40, 13.32
compact : 17.4, 17.5, 17.17
complete : 10.16
connected by paths : 16.13
connected by piecewise C¹ paths : 6.31
connected : 16.1, 16.4
connected component : 16.15
convergent sequence : 9.1, 9.8, 13.13
countably compact : 17.8
dense set : 9.51
diameter : 6.20, 6.23
first countable : 13.40
geodesic distance : 6.32
Hausdorff : 13.34
interior : 8.37, 13.32
isometry : 7.4
Klein surface : 12.19.b
neighbourhood : 8.14, 13.11
open set : 8.19, 13.3
product metric space : 12.1, 12.2, 12.3
projective plane : 6.9.c, 12.16, 12.19.c
quotient metric space : 12.8, 12.9
second countable : 13.45
sequentially closed set : 13.18
sequentially compact : 17.2
torus : 12.7.b, 12.12.fg, 12.19.a

Acknowledgements

Anabela Silva contributed with typing.

Colophon

The text is written in plain html. Simple formulas are written in html, more complicated formulas (e.g. involving fractions or roots) are written using the Mathematical Markup Language. The html editor from blogger.com has been used for quickly finding some mathematical symbols.
This script is extremely useful for managing the numbering of items and sections.
Simple drawings are produced in Paint. More complicated drawings are produced using maniFEM and gmsh.

updated on 2025.01.12