|
Se dois pontos A e B são dados num plano vertical, fazer corresponder a uma partícula móvel M o trajecto AMB pelo qual a partícula, descendo sobre o seu próprio peso, passa do ponto A para o ponto B no mais curto espaço de tempo. |
1º enunciado
do problema. Ao longo do texto, Johann formula três enunciados para o mesmo problema.
|
|
| Para suscitar nos amantes de tais coisas o desejo de se empenharem na resolução deste problema, observe-se que a questão proposta não consiste, como parece, em mera especulação sem qualquer uso. Pelo contrário, como ninguém prontamente acreditaria, tem grande utilidade noutros ramos da ciência tais como a mecânica. Entretanto, (para evitar decisões precipitadas) [importa ter em conta que] apesar de a linha recta AB ser o caminho, de facto, mais curto entre os dois pontos A e B, no entanto, não é esse o caminho percorrido no mais curto período de tempo. |
|
|
| Contudo, a curva AMB, cujo nome darei caso ninguém a tenha descoberto até ao final deste ano, é uma bem conhecida dos geómetras. | Johann refere-se à Tautochrone de Huygens
|
|
|
Proclamação Tornada Pública em Groeningen, [Janeiro], 1697 |
||
| Johann Bernoulli, professor público de matemática, presta a sua mais sincera homenagem aos mais perspicazes matemáticos de todo o mundo. Dado que é conhecido com certeza ser raro existir algo que mais grandiosamente motive espíritos nobres e engenhosos para trabalhos que levem ao aumento do conhecimento do que propor problemas simultaneamente difíceis e proveitosos, e que através da resoluções dos mesmos, e por nenhum outro modo, lhes permitam atingir a fama e construir para si próprios monumentos eternos para a posterioridade; | Johann
Bernoulli faz apelo,
não a recompensas materiais, mas sim a razões cognitivas e de
reconhecimento do mérito.
|
|
| assim, devo merecer o agradecimento do mundo matemático se, imitando o exemplo de homens como Mersenne, Pascal, Fermat, e, acima de todos, o recente e anónimo enigmatista Florentino, e outros que fizeram o mesmo antes de mim, trouxer perante os proeminentes analistas da nossa época um problema que permita, | O anónimo florentino a que Johann se refere é Vincentius Viviani e o problema por si proposto data de 1692. Para mais esclarecimentos sobre os problemas propostos pelos matemáticos referidos, clique aqui (1) | |
| qual pedra-de-toque, testar os seus métodos, exercer os seus poderes e, caso consigam dar à luz alguma descoberta, comunicar connosco de forma a que todos recebam publicamente o seu merecido reconhecimento. | Touchstone - pedra utilizada para testar a pureza de ouro ou prata. Em sentido lato, teste que permite determinar a qualidade e genuinidade de algo. | |
|
O facto é que, há meio ano atrás, no número de Junho da Acta de Leipzig, propus um desses problemas cuja utilidade, conjuntamente com a beleza, deverá ser reconhecida por todos aqueles que se apliquem com sucesso sobre o assunto. |
No entanto, Leibniz, no número de Maio de 1697 das Acta Eruditorum, p.202, afirma que terá sido Galileu quem originalmente propôs o problema de Braquistócrone. Para mais informação clique aqui (2) | |
|
Foi dado aos geómetras o prazo de seis meses desde o dia da publicação, findo o qual, se ninguém apresentasse uma solução, eu próprio havia prometido exibir a minha. |
Acabariam por ser entregues cinco soluções. Para além da de Johann, foram apresentadas nas Acta Eruditorum de 1967 soluções do seu irmão Jakob, de Leibniz e uma outra sob anonimato. Ao examinar a solução anónima, Johann terá comentado "reconheço o leão pela sua garra". Referia-se a Newton o qual, posteriomente, admitiu ter resolvido o problema. Uma outra solução foi submetida por L´Hopital. | |
|
Problema
Mecânico-Geométrico sobre a Curva de Descida mais Rápida. |
2º enunciado
do problema.
|
|
| O significado do problema é este: De entre as infinitas curvas que juntam dois pontos dados, ou que se possam descrever de um para o outro, escolher aquela que, se a curva fôr substituída por um tubo fino ou calha e por uma pequena esfera que seja lá colocada e solta, então esta [esfera] irá passar de um ponto ao outro no menor período de tempo. |
|
|
|
De forma a excluir qualquer ambiguidade, que seja expressamente compreendido que aqui aceitamos a Hipótese de
Galileu, cuja verdade, quando a fricção é neglegenciada, não causará duvidas a nenhum geómetra de bom senso: velocidades adquiridas por um corpo pesado em queda são proporcionais à raiz quadrada da altura percorrida em queda. Contudo, o nosso método de solução é completamente geral e poderia ser usado sob quaisquer outras hipóteses. Uma vez que nada de obscuro permanece, ferverosamente pedimos a todos os geómetras desta época que preparem, abordem e utilizem tudo o que mantêm escondido nos últimos recantos dos seus métodos. |
A Hipótese de Aristóteles afirma que a velocidade de queda é proporcional ao peso e inversamente proporcional à densidade do meio em que o meio caí. A Hipótese de Galileu assume que um corpo em queda acelera uniformemente, ou seja, ganha iguais quantidades de velocidade em iguais intervalos de tempo.
|
|
|
Que aquele que consiga solucionar este problema conquiste o prémio que prometemos. Obviamente, esse prémio não é ouro nem prata, prémios esses que apelam apenas a espíritos simples e venais dos quais nada há a esperar de louvável ou de útil para a ciência. Ao invés, como a virtude é nela própria a mais desejada recompensa e a fama um poderoso incentivo, oferecemos àquele homem de nobre sangue,
um prémio, composto por honras, elogios e aplausos; assim coroaremos, honraremos e exaltaremos, pública e privadamente, por carta e por palavra, a perspicácia do nosso grande
Apollo.
Se, contudo, passar a época da Páscoa e ninguém se apresentar como tendo resolvido o nosso problema, então não reteremos por mais tempo a nossa solução. |
Johann continua a exaltar as nobres recompensas e motivos para abordar este problema | |
| Se os geómetras estudarem estas soluções, que são desenhadas a partir de fontes profundas e obscuras, não temos dúvidas que irão apreciar as estreitas fronteiras da geometria vulgar e valorizar tantro mais a nossa descoberta, quanto poucos são os que apareceram para resolver o nosso extraordinário problema; | Johann mostra estar consciente do novo ramo da matemática que descobrira e da sua importância. | |
| E, mesmo entre esses, que proclamam métodos especiais que recomendam como elevados, os nossos
métodos, não só penetraram nos mais profundos segredos da geometria, como alargaram as suas fronteiras de forma maravilhosa; ainda que, os seus preciosos teoremas, que imaginam desconhecidos por todos, tenham sido publicados por outros já há muito
tempo. |
Johann refere-se à polémica que opunha Leibniz a Newton. Na verdade, enquanto Leibniz publicava o seu trabalho sobre o Cálculo, trabalho este que encontrou grande entusiasmo por parte dos Bernoulli, Newton estudava e mantinha em segredo as suas descobertas sobre fluxos. Daí que seja possível dizer que a apresentação do problema de Braquistócrone visava saber quanto Newton tinha avançado nas suas investigações. |
|
| A curvatura de um raio de luz num ambiente não-uniforme, e a solução do problema proposto na Acta de 1696, p. 269, de descobrir a Braquistócrone, i.e., a curva ao longo da qual uma partícula pesada desliza verticalmente de um ponto dado para um outro ponto dado no mais curto período de tempo; e a construção da Sincrone, ou a frente do raio. | ||
| Até os nossos dias apareceram tantos métodos que lidam com máximos e mínimos que, aparentemente, não permanece nada de subtil em relação a esta matéria que não possa ser discernida esses métodos - assim pensam aqueles que se orgulham por serem os criadores desses métodos ou aqueles que são seus seguidores. Agora, podem os estudantes jurar quanto quiserem pela palavra do seu mestre, que ainda assim, se fizerem apenas um esforço, verão que o nosso problema não pode ser forçado para dentro das limitadas fronteiras impostas pelos seus métodos, que abrangem somente a determinação de máximos e mínimos dentro de certas quantidades em número finito ou infinito. De facto, onde as próprias quantidades envolvidas no nosso problema, de onde serão descobertos máximos e mínimos, não estão mais determinadas que aquilo que se procura - esta é uma tarefa, uma ardúa tarefa! |
Em todo este parágrafo, Johann mostra estar consciente de que descobrira uma nova área na matemática, o cálculo de variações. Referindo-se aos métodos desenvolvidos por Descartes e Fermat sobre o tema dos extremos, Johann descreve aquele que é o tema central do Cálculo de Variações: a análise de extremos mas cujas variáveis, em oposição ao cálculo introdutório, são funções. |
|
|
Mesmo homens distintos
como Descartes, Fermat e outros, que em tempos disputaram tão vigorosamente pela superioridade dos seus métodos como se disputassem por Deus e
terra, ou agora, nos seus lugares, os seus discípulos, necessitam de confessar sinceramente que os métodos disponíveis por essas mesmas autoridades são aqui inteiramente inadequados.
Não é da minha natureza nem meu propósito ridicularizar as descobertas de outros. Estes homens, certamente, muito conseguiram e atingiram de forma admirável o objectivo por eles estabelecido. No entanto, porque não encontramos quaisquer considerações sobre este tipo de máximos e mínimos nos seus legados escritos, não recomendaram assim, os seus métodos para outros senão os problemas usuais. |
Descartes e Fermat mantiveram de facto uma vigorosa disputa sobre máximos e mínimos.
|
|
|
Não proponho apresentar um método universal, [algo] que poderá ser uma vã procura; mas antes, métodos particulares de proceder pelos quais, felizmente, decifrei este problema. Métodos que são, de facto, bem sucedidos, não só neste problema mas em muitos outros também. |
||
| Nesse sentido, decidi submeter a minha solução ao celebrado
Leibniz, enquanto outros procuravam outras soluções, para que ele pudesse publicá-la juntamente com a sua própria, caso descobrisse
alguma, situação de que não duvido pois estou a par do génio deste homem sagaz.
De facto, enquanto escrevo isto, sei através de uma das suas cartas, com que ele frequentemente me honra, que o meu problema
lhe agradou para além das [minhas] expectativas, e (dado que o atraíu pela sua beleza, como ele o diz, como a maçã atraíu Eva) imediatamente ficou detentor da solução. O futuro revelará o que outros terão
conseguido. Em todo o caso, o problema merece que os geómetras lhe dediquem algum tempo à sua resolução, pois um homem como Leibniz, tão ocupado com outras tarefas, não pensou ser inútil dedicar-lhe o seu. |
|
|
|
E é recompensa suficiente para eles, se o resolverem, que obtenham acesso a verdades escondidas que dificilmente de outra forma se aperceberiam. |
Insistência de Johann no seu apelo e na virtuosa recompensa. |
|
| Com justiça admiramos Huygens porque ele foi o primeiro a descobrir que uma partícula pesada descreve na queda uma ciclóide comum, dispendendo o mesmo tempo, qualquer que seja o ponto de onde a ciclóide começa o seu movimento. Mas ficarão petrificados de espanto quando eu disser que, precisamente esta Ciclóide, a Tautócrone de Huygens é a nossa Braquistócrone pedida. |
Sobre a ligação entre a Braquistócrone, a Tautochrone e as Ciclóides em
geral, saiba
mais (3) |
|
| Cheguei a este resultado por meio de dois caminhos distintos, um indirecto e outro directo. Ao seguir o primeiro [caminho], descobri uma maravilhosa relação entre a órbita curva de um raio de luz num meio continuamente variável e a nossa curva Braquistócrone. Observei ainda outras coisas sob as quais não sei o que se esconde de que será útil para a dióptrica. Consequentemente, o que afirmei quando propus o problema é verdade, nomeadamente, que não era mera especulação mas que se provaria bastante útil para outros ramos da ciência, como por exemplo para a dióptrica. Mas, como o que se diz é confirmado pelo próprio problema, aqui está o primeiro método de resolução! | Johann declara ser detentor de duas soluções, uma indirecta e outra
directa: o primeiro método, indirecto, utiliza uma analogia com um raio de
luz; o segundo, directo, parte da Hipótese de Galileu.
Neste momento, Johann vai resolver o problema de forma indirecta estabelecendo uma analogia entre o seu problema e a trajectória de um raio de luz. |
|
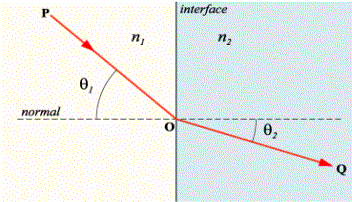
| Fermat demonstrou numa cara a La Chambre que uma raio de luz que passe de um meio raro para um meio denso é curvado pela normal, de forma a que o raio (que por hipótese procede sucessivamente da fonte de luz para o ponto iluminado) descreva o trajecto que é mais curto em tempo. A partir deste princípio, ele mostra que o seno do ângulo de incidência e que o seno do ângulo de refracção são directamente proporcionais à raridade do meio, ou aos reciprocos das densidades; ou seja, na mesma proporção das velocidades com que o raio atravessa os meios. | Os princípios
referidos são o "princípio
do menor tempo enunciado por Fermat e a Lei de Snell. Para mais
desenvolvimentos, clique aqui (4)
|
|
| Mais tarde, o perspicaz Leibniz, na Acta Eruditorum, 1682, p. 185 et. seq., e, pouco depois, o celebrado Huygens no seu tratado De Lumine, p. 40, provaram em detalhe e justificaram pelos mais convincentes argumentos este mesmo princípio físico, ou aliás metafísico, que Fermat, satisfeito com a sua prova geométrica e muito lesto a renunciar à validade do seu princípio do menor tempo, aparentemente abandonou sob a pressão de Clerselier. |
Suporte histórico para esta afirmação de Bernoulli (5)
|
|
|
Se agora considerarmos um meio que não seja uniformemente denso mas [que seja] como se separado por um número infinito de planos deitados horizontalmente, um debaixo do outro, cujos interstícios estão preenchidos com material transparente, cuja raridade aumenta ou decresce variando consoante uma certa lei; então é claro que um raio possa ser considerado como uma pequena esfera que se move, não numa linha recta, mas sim numa linha curva. (O acima mencionado Huygens anota isto no seu tratado
De Lumine mas não determina a natureza da curva.) Este trajecto é tal que a partícula que o atravessa com cuja velocidade aumenta ou diminui continuamente em proporção à raridade, passa de um ponto ao outro no menor espaço de tempo. Dado que os senos [dos ângulos] de refracção em cada ponto são respectivos à raridade do meio ou às velocidades da partícula, é também evidente que essa curva terá essa propriedade, que os senos [dos ângulos] de inclinação na vertical serão sempre proporcionais às velocidades. Posto isto, repara-se sem dificuldade que a Braquistócrone é a curva que seria traçada por um raio de luz na sua passagem por um meio cuja raridade é proporcional à velocidade que uma partícula pesada atinge em queda vertical. Pois, quer o aumento de velocidade esteja dependente da natureza do meio, mais ou menos resistente, assim como no caso do raio de luz, ou quer se remova o meio, e supõe-se que a aceleração é produzida por meio de outro agente mas de acordo com a mesma lei, assim como no caso da gravidade; como em ambos os casos a curva é supostamente percorrida no menor espaço de tempo, o que nos impede de substituir um no lugar do outro? |
||
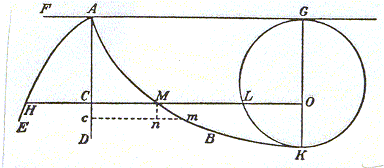
| Desta forma podemos resolver o nosso problema na forma geral, assumindo uma qualquer lei da acelaração. Porque é reduzido a descobrir o trajecto curvo de um raio de luz num meio cuja raridade varia arbitrariamente. Assim seja FGD o meio, limitado pela horizontal FG
no qual[está situado] o ponto originário A.
|
||
Seja a vertical AD o eixo de uma curva dada AHE, cuja associada HC determina a raridade do meio na altura AC, ou a velocidade do raio, ou corpúsculo, nos pontos M. Seja AMB o raio curvo que se procura. Chame-se AC, x; CH, t; CM, y; o diferencial Cc, dx; diff. Nm, dy; diff. Mm, dz; e seja a uma constante arbitrária. Tome-se Mn para o seno inteiro, (13) mn para o seno do ângulo de refracção ou de inclinação da curva em relação à vertical, e assim pelo que foi acabado de dizer, mn está para HC numa proporção constante, ou seja, dy : t = dz : a. Isto dá-nos a equação a . dy = t . dz, ou a . a .
dy2 = t . t . dz2 = t . t . dx2 + t . t .
dy2; que quando reduzida dá a equação diferencial geral dy = t . dx : para a curva AMB. Assim, e de uma única vez, resolvi dois notáveis problemas, um óptico e outro mecânico, e [consegui] mais do que havia pedido a outros; demonstrei que dois problemas de àreas completamente distintas da matemática são contudo da mesma natureza. |
||
Vamos agora considerar um caso especial, nomeadamente aquele que surge da hipótese usual incialmente introduzida e provada por Galileu, de acordo com a qual a velocidade de um corpo pesado em queda varia consoante a raiz quadrada da distância percorrida; pois este é, de facto, o problema. Sobre esta suposição a curva AHE será uma parábola, ou seja, t.t = a.x e t = . Se esta é substítuida na equação geral
descobre-
se que dy = dx .  ,
da qual concluo que a curva Braquistócrone é a Ciclóide vulgar. De
facto, se rolarmos o círculo GLK,
cujo diâmetro é a, por AG, e se o início da rotação se dá no próprio A; então o ponto K
descreve uma ciclóide, que se descobre ter a mesma equação diferencial dy
= dx . |
Demonstração do segundo método, directo, utilizando a Hipótese de Galileu.
|
|
|
também (a . dx – 2 . x . dx) : 2 . teremos y ou CM = GL – LO, e assim MO = CO – GL + LO. Dado que (assumindo CO = semiperímetro GLK) CO – GL = LK, tem-se MO = LK + LO, e, cancelando LO, ML = LK; o que mostra que a curva KMA é a Ciclóide. |
A palavra
soma é aqui utilizada como Integral;
A título de
curiosidade, foi num manuscrito datado de 29 de Outubro de 1675, que
Leibniz introduziu o símbolo que actualmente se utiliza para representar
o integral. O símbolo 
que tanto utilizamos, sugeria a Leibniz a primeira letra da palavra
latina summa, isto é, soma. A meio
do seu trabalho sobre integrações por somas dos indivisíveis de
Cavalieri, abreviou “omnes lineae”,
ie, todas as linhas, com “omn 1”.
Comentou na altura, “Será útil escrever
para omn,
ie, a soma dos 1. No mesmo dia, introduziu o símbolo da diferencial “d”. |
|
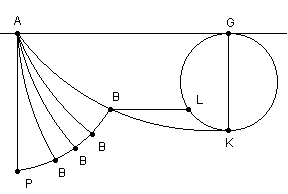
| Por forma a solucionar completamente o problema temos de mostrar ainda como de um dado ponto, como vértice, se pode desenhar a Braquistócrone, ou Ciclóide, que passa por um segundo ponto dado. Isto é facilmente conseguido pelo seguinte; Unem-se os dois pontos dados A, B, pela recta AB, e descreve-se uma Ciclóide arbitrária na horizontal AL, tendo como ponto inicial A e intersectando a recta AB no ponto R; então, o diâmetro do círculo que descreve a Ciclóide pretendida ABL e que passa por B está para o diâmetro do círculo que descreve a Ciclóide ARS assim como AB está para AR. | ||
| Antes de concluir, não posso deixar de expressar mais uma vez a admiração que experimentei sobre esta inesperada identidade da Tautochrone de Huygens e da nossa Braquistócrone. | Johann faz agora algumas considerações sobre a sua descoberta e sobre a Brachistochrone. | |
| Mais, penso que seja merecedor de atenção que esta identidade seja encontrada apenas sob a Hipótese de Galileu, para que, a partir disto, se possa conjecturar que a natureza assim o queria. Pois, como a natureza está acostumada a proceder de forma mais elementar, aqui consegue dois serviços diferentes através de uma única curva, enquanto sobre outra qualquer hipótese duas curvas seriam necessárias, uma para oscilações de igual duração, outra para a curva de mais rápida descida. |
Estão aqui subjacenbtes dois grandes princípios metafísicos: razão suficiente e simplicidade
|
|
| Se, por exemplo, a velocidade de queda de um corpo variasse não como a raiz quadrada mas como a raiz cúbica da altura [percorrida], então a Braquistócrone seria algébrica, a Tautochrone por outro lado seria transcendente; mas, se a velocidade variasse com a altura [percorrida] então as curvas seriam algébricas, uma seria um círculo, a outra uma linha recta. | Johann levanta agora duas outras conjecturas | |
|
Acredito que os geómetras não ficarão ingratos se, em conclusão, eu der a solução de
um outro problema, apenas como merecedor de consideração, que me ocorreu enquanto escrevia o que está para trás. horizontal e AP a vertical. O significado do problema é o seguinte, que para qualquer ciclóide descrita em AG, uma porção AB seja considerada, tal que a partícula pesada que desce de A necessitasse o mesmo tempo a atravessa-la como necessitaria para na queda de uma dada altura vertical AP; quando isto é conseguido, o ponto B estará na curva Sincrone PB que se procura. |
Johann apresenta ainda outro problema, que deixa parcialmente em aberto. | |
, designando AC, x, e CM, y. Este facto
também se
=
x.dx :
,
