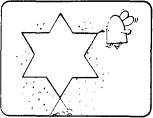
A curva "cristal-de-neve"
é uma figura paradoxal, mas não impossível.
A construção inicia-se com a forma de um
triângulo equilátero. Ao desenhar um triângulo sombreado no terço central de
cada um dos lados do triângulo original, obtém-se uma estrela
de seis pontas.

Repetindo a operação, desenhando triângulos cada
vez mais pequenos nos lados da estrela, a
curva vai-se tornando cada vez mais extensa e
ganhando a forma de um cristal-de-neve.
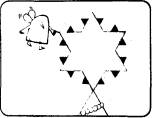

A curva "cristal-de-neve" é uma das mais belas de uma classe de curvas
designadas por patológicas devido às suas
características paradoxais. Prosseguindo a
construção do cristal-de-neve ad infinitum, o comprimento dessa curva
tenderá para o infinito, sem deixar, no entanto, de delimitar uma área finita!
Dito de outra forma, os sucessivos comprimentos da curva, em cada fase de
construção, formam uma série divergente, enquanto as sucessivas áreas
englobadas pela curva formam uma série que converge para 8/5 da área do triângulo
original!
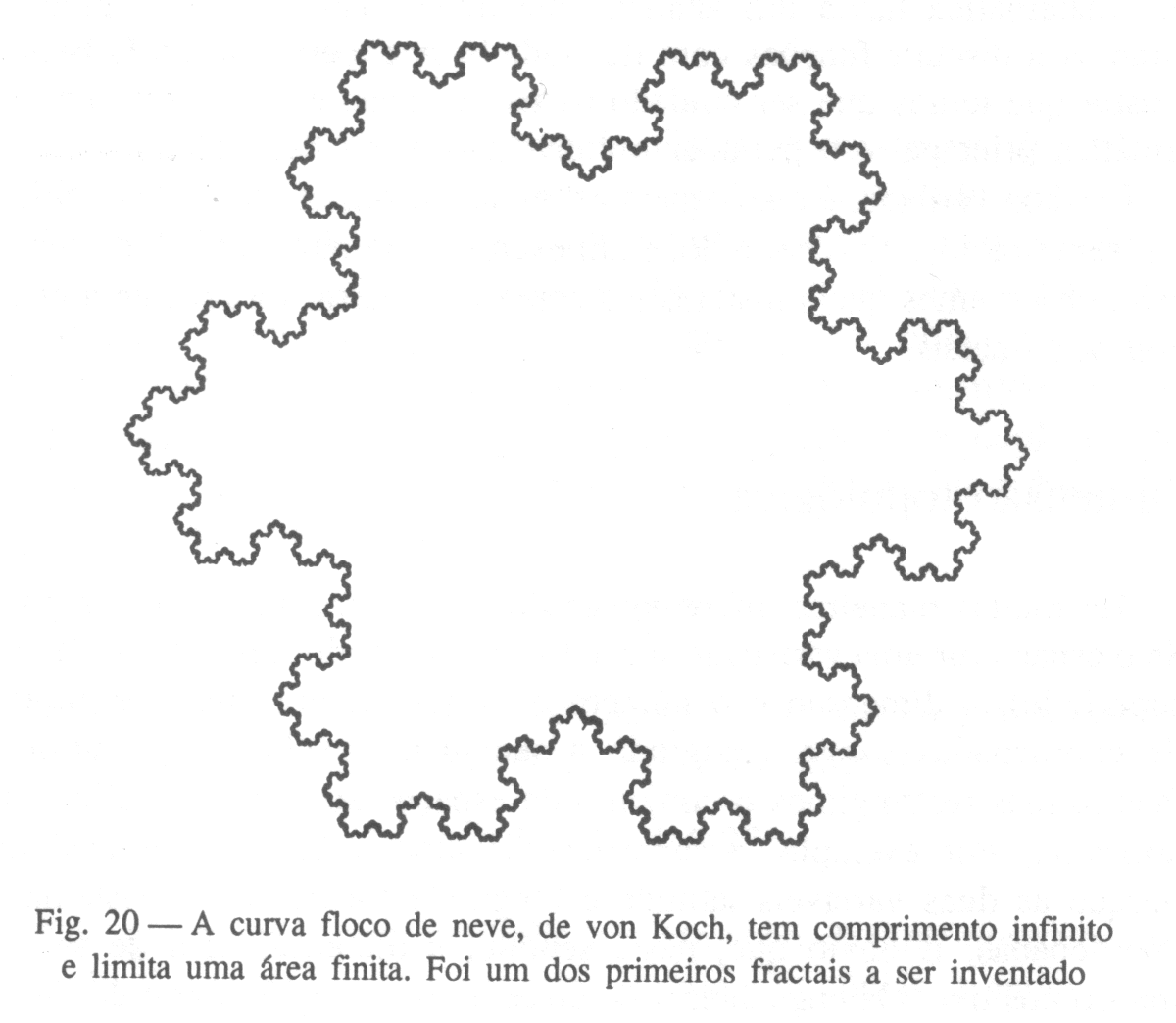
(Retirado de Stewart, 1996, p. 199)