O Rectângulo de ouro é um ser matemático que ultrapassa as fronteiras da matemática sendo utilizado em áres tão diversas como a arquitectura, a compreensão da natureza ou a publicidade
Vejamos como se constrói o rectângulo de ouro
-
Dado um segmento [AC], tal que B divida o segmento de acordo com a proporção de ouro, constroi-se o quadrado [ABCD]
(i) ![]()
![]()
(ii) 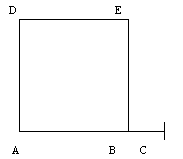
-
Traça-se [CF] perpendicular a [AC]
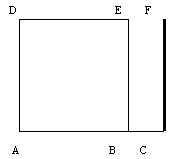
-
Prolonga-se o lado [DE] de forma a que este intersecte [CF] no ponto F
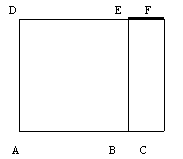
A figura [ACDF] é o rectângulo de ouro.
Luca Pacioli, matemático e humanista italiano, nascido em Florença em 1445, autor de diversas obras de enorme difusão entre matemáticos e pintores do séc. XVI,: Entre elas, destaca-se o tratado "De Divina Proportione" (1509) no qual aparece o rectângulo de ouro.
Um exemplo do rectângulo de ouro que aparece em De Divina Proportione
Sejam 3 rectângulos de ouro que se intersectam simetricamente e, cada um deles, perpendicularmente aos outros 2. Os vértices desses 3 rectângulos coincidem com os 12 vértices de um icosaedro regular.
Foi a partir deste tratado que Leonardo Da Vinci mostrou de que modo a proporção de ouro se encontra relacionada com a estrutura do corpo humano. A utilização desta proporção na pintura ficou conhecida como a técnica da simetria dinâmica.
Outras notas sobre o rectângulo de ouro:
-
Muitas embalagens têm a configuração do rectângulo de ouro
-
O cartão de crédito tem um tamanho próximo do número de ouro
-
O rectângulo de ouro está interligado com outros conceitos matemáticos, tais como séries infinitas, decágono regular, sólidos platónicos, espirais equiangulares e logaritmicas, limites, triângulo de ouro e pentágono.
Um exemplo do rectângulo de ouro da arte Grega
Também os arquitectos e artistas da Grécia Antiga sentiram que a razão de ouro e o rectângulo de ouro potenciavam o valor estético dos monumentos e das esculturas. Conheciam a razão de ouro, como construi-la, como obter aproximações e como usá-la para construir o rectângulo de ouro.
O Parténon ilustra maravilhoasamente o uso arquitectónico do rectângulo de ouro
