O cálculo lógico é um pressuposto de qualquer cálculo e sem o seu auxílio nenhuma demonstração poderia ser feita. O que uma teoria axiomática faz é sobrepor-se à lógica, acrescentando algumas constantes (não lógicas) específicas e alguns axiomas (não lógicos) necessários para a dedução de novos resultados. Esses axiomas não lógicos, específicos da teoria, são dados como premissas para outras deduções. São fórmulas que não têm o carácter de "verdades lógicas" mas sim de "verdades aceites". A sua função é a de se constituírem como base para deduções de resultados que a lógica por si só não poderia permitir.
Dizemos que uma fórmula é logicamente válida quando puder ser deduzida dos axiomas lógicos. Ao lado das fórmulas logicamente válidas, existem fórmulas designadas simplesmente como válidas. Não há método uniforme para as caracterizar. O mais comum, é seleccionar um conjunto (finito ou não) de proposições que são chamadas axiomas não lógicos e dizer que uma proposição é válida se e só se puder ser deduzida desse conjunto. Por outras palavras, a proposição f será válida se e só se puder ser deduzida dos axiomas (lógicos e não lógicos) admitidos por esta teoria.
As teorias em que a noção de validade tiver sido introduzida dessa maneira dir-se-ão teorias axiomáticas. Quando a teoria tiver sido axiomatizada, diz-se que as proposições válidas são proposições demonstradas (ou demonstráveis).
Uma teoria formalizada, salvo se apresentada directamente como sistema axiomático (caso em que as suas proposições válidas se identificam com as proposições demonstráveis nesse sistema) pode ou não ser axiomatizada. Entre as teorias axiomáticas, um grupo particularmente notável é aquele que é composto por teorias com um número finito de axiomas.
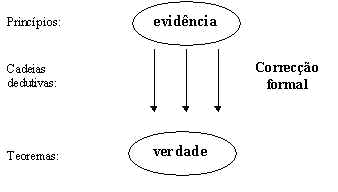
De acordo com o logicismo, partimos de um conjunto de axiomas, postulados e definições tidos como verdades evidentes, dos quais, garantidos a correcção e o rigor formais, se chega à verdade da conclusão.
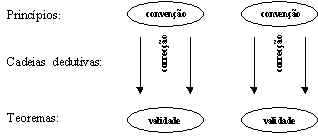
Segundo o axiomatismo, partimos de axiomas, postulados e definições que são considerados como puras convenções e deles deduzimos teoremas cuja validade depende das convenções iniciais e do rigor das cadeias dedutivas.
Esquematicamente, temos:
Logicismo
Axiomatismo