As Três Leis de Kepler
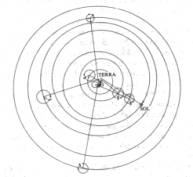
O movimento dos planetas, estrelas e outros corpos celestes têm sido observados desde há muito tempo. Na antiguidade pensava-se que a Terra estava no centro do Universo. Este Modelo Geocêntrico foi elaborado e formalizado pelo astrónomo grego Ptolomeu (100-170) e aceite durante 1400 anos.

Figura: Sistema ptolemaico
Em 1543, Copérnico (1473-1543) sugeriu que a Terra e os outros planetas teriam órbitas circulares em torno do Sol: Modelo Heliocêntrico.
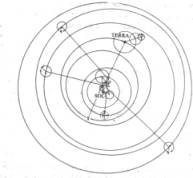
Figura: Sistema copernicano.
O astrónomo dinamarquês Tycho Brahe (1546-1601) realizou medidas astronómicas durante 20 anos sendo de notar que as suas observações precisas de planetas e de 777 estrelas visíveis a olho nú foram feitas sem utilizar o telescópio, então não ainda inventado.
As observações realizadas por Tycho Brahe
tornaram-se infinitamente mais valiosas para o progresso da ciência depois de
trabalhadas por Kepler. Quando Kepler se tornou sucessor de Tycho, herdou a
maior e mais cuidada colecção de observações planetárias, em especial do
planeta Marte, que alguma vez se tinha conseguido reunir.
Kepler passou cerca de dezasseis anos a tentar chegar a uma
dedução matemática do modelo do movimento dos planetas que justificasse as
observações realizadas pelo seu mestre. A análise de Kepler mostra que a ideia de existência de
órbitas circulares tinha de ser abandonada, contrariando assim a teoria
defendida por Tycho que, em carta enviada havia escrito1:
"É necessário que
as órbitas dos planetas sejam completamente descritas por movimentos circulares
pois, caso contrário, eles não regressariam perpétua e uniformemente à sua
órbita e a sua perpetuidade seria perturbada (...) uma mente racional iria
retrair-se com horror face tal suposição [a não circularidade] (...) se o
movimento circular nos céus, devido à sua disposição, por vezes aparenta
produzir - para alguém que tenha a vã curiosidade de reparar em tais
particularidades - diversas figuras angulares na sua maioria de forma oblonga,
então isso pode ter sido por acaso." 2
Kepler descobriu, em 1605, que a órbita de Marte só podia ser descrita por uma elipse. Citando Kuhn3: "Uma longa série de tentativas sem sucesso forçou Kepler a concluir que nenhum sistema baseado em círculos compostos resolveria o problema. Uma outra figura geométrica deveria, pensou, conter a chave. Tentou vários tipos de ovais, mas nenhum eliminou as discrepâncias entre a sua hipótese de teoria e a observação. Então, reparou que as próprias discrepâncias variavam de um forma matemática familiar e, ao investigar essa irregularidade descobriu que a teoria e a observação podiam ser conciliadas se os planetas se movessem em órbitas elípticas com velocidades variáveis."
Kepler generalizou esta análise para todos os planetas e, em 1605, enunciou a Primeira Lei :
Lei da órbitas elípticas
Todos os planetas se
movem segundo órbitas elípticas com o Sol num dos pontos focais.
No entanto, em 1602,
quando tentava calcular a posição da Terra na sua órbita, Kepler havia já
definido aquela que viria a ser a sua Segunda Lei
Lei da áreas
À medida que o planeta
descreve a sua órbita, o seu vector posicional relativamente ao Sol percorre
áreas iguais em intervalos de tempo iguais.
Uma demonstração desta Lei é apresentada por Serway4:
Considere-se um planeta de massa Mp que se move em torno do Sol em órbita elíptica:
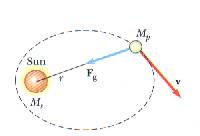
Figura: A força gravitacional que actua num
planeta dirige-se para o Sol, ao longo do vector direccional.
A força gravitacional actua no planeta sempre ao longo do vector posicional, com direcção para o Sol. A força dirigida para dentro ou para fora de um ponto fixo é chamada de força central (que é apenas função do raio). O momento da força que actua no planeta devido a esta força central é obviamente zero, desde que F seja paralelo a r. Ou seja,
![]()
Como ![]() e
e ![]() , o momento angular
de um planeta é
, o momento angular
de um planeta é
uma constante do movimento:
![]() constante
constante
Dado que L é uma constante
do movimento, o movimento dos planetas em qualquer instante é restringido ao
plano formado por r e v.
Pode-se relacionar este resultado com as seguintes
considerações geométricas. O vector posicional r na figura seguinte descreve
uma área no intervalo de tempo . Esta área é igual a metade da área ![]() de um paralelogramo formado pelos vectores r e
de um paralelogramo formado pelos vectores r e ![]() .
.
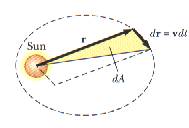
Figura: Como um planeta orbita em torno do Sol, a área descrita pelo vector direccional no tempo dt é igual a metade da área do paralelogramo formada pelos vectores r e dr = v dt.
Como o deslocamento do planeta no
intervalo de tempo ![]() é
é ![]() ,
obtém-se:
,
obtém-se:
![]()
![]() constante
constante
em que L e Mp são constantes do movimento. Assim, o vector posicional do Sol ao planeta descreve áreas iguais em intervalos de tempo iguais (Segunda Lei de Kepler).
A primeira e a segunda leis de Kepler, embora descobertas em 1605 e 1602, respectivamente, apenas foram publicadas em 1609 na obra intitulada "Astronomia Nova".
A Terceira
Lei estabelece uma
relação entre os tempos periódicos em que os planetas completam as suas
órbitas em torno do Sol e as suas distâncias médias ao Sol.
Kepler começou por tentar estabelecer uma relação entre D (distância do
planeta ao Sol) e T (período sideral do planeta), e depois entre D e T2 não
tendo conseguido chegar a nenhuma conclusão satisfatória. O mesmo aconteceu
quando considerou T2 e D2. Mas quando tentou relacionar T2 e D3 a situação
mudou , tal como se pode observar pela tabela seguinte:
| Mercúrio | Vénus | Terra | Marte | Júpiter | Saturno | |
| Semi-eixo maior(UA) | 0,387 | 0,723 | 1,000 | 1,524 | 5,203 | 9,534 |
| Período(anos) | 0,241 | 0,615 | 1,000 | 1,881 | 11,862 | 29,456 |
| T2 (U.A.) | 0,058 | 0,378 | 1,00 | 3,53 | 141 | 867,7 |
| D3 (U.A.) | 0,058 | 0,378 | 1,00 | 3,54 | 141 | 867,9 |
E assim formulou a sua Terceira Lei:
Lei Harmónica
Os quadrados dos tempos de revolução de quaisquer dois planetas em torno do Sol (incluindo a Terra) são proporcionais aos cubos das suas distâncias médias ao Sol.
Esta lei estabelece que os planetas com
órbitas maiores se movem mais lentamente em torno do Sol. O que implica que a força entre o Sol e o planeta decresce com a distância ao Sol.
Sendo T o período sideral do planeta, D o semi-eixo maior da
órbita que é igual à distância média do planeta ao Sol, e K uma constante,
podemos expressar a 3ª lei como:
![]()
Esta lei significa
que
é impossível que, em qualquer sistema de satélites, estes se movam a qualquer
velocidade ou a qualquer distância, dado que uma vez escolhida a distância a
velocidade está necessariamente determinada.
É lei é conhecida por Lei Harmónica uma vez que, quando
Kepler a descobriu, pensou que demostrava a verdadeira harmonia celeste. Foi
publicada em 1619 em "Harmonices Mundi", tendo
exercido um influência decisiva na formação da teoria da atracção universal
de Newton.
Serway 5 apresenta a seguionte demonstração da Terceira Lei de Kepler:
Considere-se um planeta de massa Mp que se move em torno do Sol, de massa MS, numa órbita circular, tal como mostra a figura seguinte:
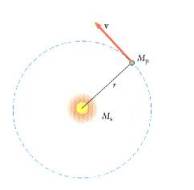
Figura - Um planeta de massa Mp move-se segundo um órbita circular em torno do Sol. A órbita de todos os planetas, com a excepção de Marte, Mercúrio e Plutão são aproximadamente circulares.
Dado que a força gravitacional exercida no planeta pelo Sol é igual à força central necessária para fazer com que o planeta se mova circularmente, tem-se:
![]()
Como a velocidade orbital
do planeta é dada por ![]() ,
,
em que T é o período, a expressão anterior fica:
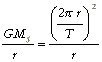
Simplificando, chega-se então à expressão final:
![]() Equação 1
Equação 1
onde KS é uma constante dada por:
![]()
A equação 1 representa a Terceira Lei de Kepler. A lei também é válida para órbitas elípticas substituindo r pelo comprimento do semi eixo-maior da elipse, a .
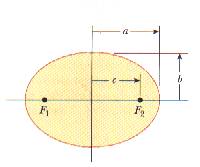
Figura: Esquema de uma elipse. O semi-eixo maior tem um comprimento a, e o semi-eixo menor tem um comprimento b. Os pontos focais estão a uma distância c do centro, com a2 = b2+c2, e a excentricidade é definida por e = c/a
Note-se
que a constante de proporcionalidade Ks, é independente da massa do
planeta. Deste modo, esta equação é válida para qualquer planeta. Se se
considerar a órbita de um satélite em torno da Terra, como a Lua, então a
constante terá um outro valor, substituindo a massa do Sol pela massa da Terra.
Neste caso, a constante de proporcionalidade será ![]() .
.
Referências:
1
Kozhamthadam, J. (1994); "The discovery ok
Keples's laws: the interaction of science, philosophy and religion";
University of Notre Dame Press; Notre Dame; London , p. 202
2 Tradução das autoras.
3 Kuhn, T. (1957); "A revolução copernicana - A astronomia
planetária no desenvolvimento do pensamento ocidental"; Edições 70;
Lisboa, p.244
4 Serway, R.; (1996); "Physics for Scientists and Engineers";
4ª Edição; USA: Saunders Golden Sunburst Series, p. 399
5 Serway, R.; (1996); "Physics for Scientists and Engineers";
4ª Edição; USA: Saunders Golden Sunburst Series, p. 398