Do século III a.C. ao século XXI...

            Aproximadamente em 300 a. C., Euclides escreveu os Elementos. 

            No século I a.C., Possidónio apresentou uma definição de paralelismo segundo a qual as rectas paralelas são as rectas equidistantes, ou seja, duas linhas rectas são paralelas se a distância medida numa qualquer perpendicular de uma delas, for sempre igual, independentemente da perpendicular escolhida. Assumir isto é equivalente a pressupor o quinto postulado e, por isso, as demonstrações baseadas nesta definição não estavam correctas.

            Proclus, no século V, criticou esta definição de Possidónio e apontou o facto de que é plausível a ideia do quinto postulado não se verificar pois há linhas como a hipérbole  que convergem para as suas assimptotas mas não chegam a intersectar-se. No entanto, Proclus acreditou que o quinto postulado era demonstrável e disse que outros antes dele haviam afirmado o mesmo.  No seu comentário ao primeiro livro dos Elementos, Proclus apresentou uma tentativa de demonstração do quinto postulado por Ptolomeu (século II), que  identifica como errada, e a sua própria tentativa de demonstração que falha ao pressupor que a distância entre duas linhas paralelas é sempre inferior a uma distância fixa (ainda que possa variar), pois isso é equivalente ao quinto postulado.

Numa tradução do século XII de um comentário árabe aos elementos de Euclides de al-Nirizi (século IX), é citado Simplicius (século VI) que, num comentário seu ao primeiro livro de Euclides, terá apresentado a demonstração de Aganis, que comete o erro de assumir uma definição de paralelismo semelhante à de Possidónio. O facto de esta demonstração de Aganis chegar até nós através do comentário de um matemático árabe é sintomático da importância da Matemática árabe após a decadência da Grécia.

            No século XIII, Nasiraddin at-Tüsi, apresenta também uma demonstração do quinto postulado. Nesta demonstração, Nasiraddin supõe que se duas rectas AB e CD são cortadas por uma recta PQ que é perpendicular apenas a uma delas (por exemplo AB). Então, as distâncias medidas nas perpendiculares de AB para CD serão menores do lado em que PQ faz ângulos agudos com CD e maiores do lado em PQ faz ângulos obtusos com CD. O seu erro reside no facto desta suposição ser equivalente ao quinto postulado.

Em 1533 foi impresso pela primeira vez o Comentário de Proclus. Sob a sua influência, várias críticas surgem de alguns comentadores.

Commandino (1509-1575), cai no erro de juntar à definição de paralelismo a ideia de equidistância. No entanto, no que toca ao quinto postulado, acaba por aceitar a demonstração de Proclus que como já se referiu, está errada. Também Clavio (1537-1612), que traduziu para latim os Elementos, reproduziu e criticou a demonstração de Proclus e apresentou uma demonstração sua do quinto postulado. A sua demonstração assenta no facto de o conjunto dos pontos equidistantes de uma recta (de um lado da recta) formarem uma linha recta. Ora, supor isso, é equivalente a supor o quinto postulado. A sua demonstração acaba por ter algumas semelhanças com a de Nasiraddin.

            No século XVII, Cataldi (1548-1626) é o primeiro matemático a publicar uma obra exclusivamente dedicada à teoria das paralelas. Cataldi assume uma hipótese que é equivalente ao quinto postulado: linhas rectas não equidistantes convergem numa direcção e divergem na outra. 

            Também no século XVI, Borelli (1608-1679) e Vitale (1633-1711) irão nos seus estudos regressar à ideia de equidistância das linhas paralelas, que havia sido levantada por Possidónio.

            Quase 2000 anos passaram desde que Euclides escreveu os Elementos e o seu quinto postulado continua a gerar perplexidade pois parece ser óbvio mas os matemáticos não conseguem demonstrá-lo. A generalidade das tentativas de demonstração até aqui referidas têm em comum o facto de pressuporem alguma hipótese que se julga óbvia e que, por isso, não precisaria de demonstração. Contudo, o que essas demonstrações demonstram não é mais do que a equivalência dessas hipóteses ao quinto postulado (a maioria dessas hipóteses saem directamente do quinto postulado e estes matemáticos provam que, reciprocamente, elas implicam o quinto postulado). 

            Muitos desses matemáticos que tentaram demonstrar o quinto postulado de Euclides tiveram o cuidado de estudar e criticar as tentativas que os precederam. Apesar disso, muitos acabaram por reincidir nos mesmos erros ou em erros semelhantes. 

        Entretanto, durante o século XVII, alguns matemáticos irão aperceber-se que, se consideram alguma hipótese que não é demonstrada dos primeiros quatro postulados, então não é correcto usá-la para demonstrar o quinto postulado.

É o caso de Wallis (1616-1703), que abandona a ideia de equidistância que os matemáticos seus antecessores haviam utilizado sem sucesso para tentar demonstrar o postulado. Wallis desiste de tentar demonstrar o quinto postulado a partir unicamente dos primeiros quatro postulados e introduz um axioma que considera ser mais plausível que o quinto postulado: sobre um segmento é sempre possível construir um triângulo semelhante a um triângulo dado. Wallis demonstra com sucesso o quinto postulado, mas está a utilizar um axioma alternativo, portanto o que está a provar é equivalência desse axioma ao quinto postulado (porque reciprocamente, o quinto postulado implica aquele axioma).  Na sua demonstração do quinto postulado, Wallis ao provar que uma determinada hipótese é equivalente ao quinto postulado, acaba pois por não fazer algo muito diferente dos seus antecessores. Contudo, é de destacar o facto de estar consciente disso e apresentar o seu axioma como alternativa ao quinto postulado.

Um outro matemático que se dedicou muito a tentar demonstrar o quinto postulado de Euclides e que deu um passo largo no caminho das geometrias não euclidianas, foi Gerolamo Saccheri (1667-1733).

Em primeiro lugar, Saccheri analisou e criticou muitas das tentativas de demonstrar o quinto postulado por matemáticos anteriores. Nessas análises, Saccheri sublinhou que tudo tinha que ser demonstrado e que, portanto, não fazia sentido tomar certas hipóteses sem as demonstrar, como haviam feito muitos matemáticos anteriores. Saccheri não cometeu esse erro. 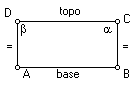Profundamente convicto de que poderia demonstrar o quinto postulado, embrenhou-se num longo estudo com esse objectivo, sem nunca considerar o quinto postulado. Começou por considerar um tipo especial de quadriláteros (os quadriláteros de Saccheri), que se caracterizam por ter um par de lados opostos iguais e perpendiculares a um terceiro lado. Este lado chama-se base e o oposto é o topo. Os ângulos a e b são os ângulos de topo. Intuitivamente, a tendência será dizer que é óbvio que estes quadriláteros são rectângulos e os ângulos a e b têm de ser rectos. Contudo, por incrível que pareça, se não for considerado o quinto postulado, essa afirmação não pode ser provada!

Saccheri provou várias equivalências ao quinto postulado: todos os quadriláteros de Saccheri são rectângulos; existe pelo menos um rectângulo (!); a soma dos ângulos internos de um triângulo é 180º. Nesse sentido, Saccheri procurou provar que os quadriláteros por ele inventados seriam rectângulos mesmo que não se considerasse o quinto postulado. Primeiro, provou que os ângulos de topo teriam que ser congruentes e que, por isso, teriam que ser ambos rectos, ambos agudos ou ambos obtusos. Então, procedeu a uma demonstração por redução ao absurdo: considerou três hipóteses  consoante os ângulos (a hipótese do angulo agudo (HAA), a hipótese do angulo recto (HAR) e a hipótese do angulo obtuso(HAO)) e procurou atingir absurdos a partir de HAA e HAO, para concluir que HAR era a única possível.

O esforço de Saccheri teve sucesso ao provar que HAO levava a um absurdo. Contudo, o sucesso não foi total, pois HAA é impossível provar ser um absurdo. Ao considerar HAA, Saccheri vai estudar a geometria hiperbólica sem se aperceber disso. Na busca de absurdos, vai demonstrar propriedades desta nova geometria até chegar a um ponto em que, talvez por querer tanto que aquilo resultasse num absurdo, comete um erro na demonstração que o faz pensar ter chegado à conclusão que pretendia.

No ano da sua morte, é publicada a obra, intitulada de Euclides ab omne naevo vindicatus, o que significará algo como Euclides liberto de todos os erros. Para ele, o grande erro de Euclides era ter colocado aquele resultado como postulado e para livrá-lo dos erros tinha de demonstrá-lo. Há quem defenda que Saccheri apercebeu-se que a sua demonstração não estava absolutamente correcta e que por isso hesitou tanto antes de publicá-la.

É espantoso ver que Saccheri lançou as fundações das geometrias não euclidianas, quando tinha o único intuito de as destruir! Há quem considere que Saccheri descobriu as geometrias não euclidianas, mas simplesmente não quis acreditar.

De destacar em 1763, a realização da tese de Georg Klügel (1739-1832), que consistiu em analisar vinte e oito tentativas de demonstrar este postulado. Klügel concluiu que todas eram insatisfatórias e sugeriu que o postulado não podia ser provado e que apenas era aceite como verdadeiro por causa dos testemunhos dos nossos sentidos. Aqui, finalmente, começa a ser levantada a possibilidade de ser impossível demonstrar o quinto postulado.

Já no século XVIII, Lambert (1728-1777) estudou as investigações de Saccheri e descobriu novos resultados no âmbito da HAA. Para além disso, Lambert teve também uma aproximação semelhante à de Saccheri, ao estudar quadriláteros cujas características essenciais seriam ter pelo menos 3 ângulos rectos (quadriláteros de Lambert). Também ele contribuirá com novos resultados para a geometria não euclidiana, mas não atingirá contradição.

Nos finais do século XVIII, o estudo da teoria das paralelas, que já havia dado frutos na Itália e na Alemanha, começa a ter notáveis avanços também em França. Por esta altura, vários matemáticos famosos franceses manifestaram interesse nesta temática da teoria das paralelas e o quinto postulado, como foi o caso de D’Alembert, Lagrange, Carnot e Laplace. D’Alembert terá mesmo falado no “escândalo da geometria” a propósito do fracasso das muitas tentativas de demonstração do quinto postulado!

Destaca-se o caso de Legendre (1752-1833), um dos melhores matemáticos do seu tempo e que, de tal modo desenvolveu uma espécie de obsessão pela demonstração do quinto postulado, que durante 29 anos publicou tentativa após tentativa em várias edições do seus Élements de Géométrie.

No século XIX, começa-se a compreender que é possível uma geometria sem o quinto postulado, embora ainda se acredite que no espaço físico é a geometria euclidiana a única possível.

Há quem considere que Gauss (1777-1855) terá sido o primeiro a ter noção dessa geometria que contrariava o quinto postulado, contudo, Gauss não publicou nada sobre os seus estudos neste campo durante a sua vida. Só através de publicações póstumas, nomeadamente correspondência sua com outros matemáticos, conseguiu-se ver que também ele tinha compreendido a possibilidade do quinto postulado ser impossível de demonstrar, se bem que não aceitasse uma geometria não euclidiana como possível.

Ainda em 1799, em resposta a uma carta de Wolfgang Bolyai em que este afirmava ter demonstrado o quinto postulado, Gauss escreve (traduzindo a transcrição de Greenberg, 1980, p. 319):

Noutro momento, terá afirmado que "Eu estou a chegar mais e mais à convicção que a necessidade da nossa geometria não pode ser demonstrada, pelo menos nem por, nem para, o intelecto humano... geometria deve ser classificada, não com a aritmética, que é puramente apriorista, mas com a mecânica", o que transmite a ideia que Gauss estava a aperceber-se da possibilidade de geometrias não euclidianas (pois não pode demonstrar que só existe a euclidiana), mas achava que para a realidade física só a euclidiana faria sentido.

Vários matemáticos estudaram esta temática durante este século e “aproximaram-se” das geometrias não euclidianas, contudo, foram Janos Bolyai (1802-1860) e Nikolai Lobachevsky (1793-1856) quem descobre e corajosamente anuncia a descoberta de novas geometrias, diferentes da euclidiana. Também eles haviam tentado demonstrar o quinto postulado mas, perante o insucesso dessa tentativa tiveram a coragem de acreditar que havia uma alternativa ao que os sentidos faziam parecer ser a única hipótese.

Janos Bolyai era filho de Wolfgang Bolyai (1755-1856), um matemático que tinha-se dedicado ao estudo da teoria das paralelas e que também havia tentado provar o quinto postulado. Janos tinha aprendido matemática com o seu pai, onde revelou muito talento, mas, acabou por tornar-se oficial no exército austríaco. No entanto, isso não o impediu de investigar Matemática, nomeadamente a teoria das paralelas e o quinto postulado. Após, como tantos outros, ter fracassado em demonstrar o quinto postulado, Janos, tentou demonstrar a sua falsidade, acabando por descobrir uma geometria não euclidiana.

É interessante ler a correspondência entre pai e filho referente a esta matéria. Quando Janos diz a seu pai que está a estudar o “problema das paralelas”, Wolfgang procura desencorajá-lo, pois considera ser um caminho impossível de percorrer, revelando uma profundo desânimo pessoal nesta área da Matemática à qual tanto se havia dedicado: “Atravessei essa noite sem fim, que extinguiu toda a luz e alegria da minha vida.”. E pede ao filho que abandone esse estudo.

Ainda assim, Janos continua o seu estudo e acaba por convencer o seu pai de que está a chegar a conclusões importantes na teoria das paralelas. Wolfgang aconselha então o seu filho a publicar o mais depressa possível o seu estudo pois, “quando o tempo está maduro para certas coisas, estas aparecem em diferentes lugares”. O que de facto acontecerá neste caso em que Lobachevsky, na Rússia, descobre também ele uma geometria não euclidiana (e é Lobachevsky quem primeiro publica uma obra sobre geometria não euclidiana, em 1829). Janos terá dito: "criei um mundo novo e diferente a partir do nada"!

Em 1831, Janos publica a sua obra como apêndice a uma obra do seu pai sobre geometria. Wolfgang tinha estudado com Gauss e correspondia-se regularmente com ele (nomeadamente sobre tentativas de demonstrar o quinto postulado), logo, enviou uma cópia da obra a Gauss. Janos e Wolfgang esperaram ansiosamente pela resposta, mas o livro perdeu-se no correio. Enviaram um novo exemplar e Gauss responde que aqueles resultados, de uma geometria não euclidiana, não eram novidade para si, pois ele próprio já andava a reflectir sobre aquilo à muito tempo.

Janos não gostou do comentário de Gauss e pensou que este lhe quisesse retirar o crédito da descoberta. Terá ficado de tal modo deprimido que não voltou a publicar nada da sua pesquisa neste campo. Nem Bolyai nem Lobachevsky chegaram a ver o seu valor reconhecido pela grande descoberta que fizeram.

Estes dois matemáticos apenas descobriram uma geometria não euclidiana, outras, como a elíptica (para esta geometria não basta negar o quinto postulado), foram descobertas mais tarde. Muitos outros matemáticos vieram a distinguir-se no campo das geometrias não euclidianas.

Em 1868, Beltrami prova a consistência de uma geometria não euclidiana, ao provar que se a geometria euclidiana é consistente, também o é a geometria hiperbólica. Deste modo, provou que era impossível demonstrar o quinto postulado pois, provou que não havia contradição lógica em considerar os quatro primeiros postulados e um quinto que contrariasse o quinto postulado de Euclides.

  Seria de esperar, que após Beltrami provar que era impossível demonstrar o quinto postulado, que ninguém voltaria a tentar o mesmo (pelo menos se tivesse conhecimentos científicos). Contudo isso voltou a acontecer. Apresento os dois exemplos que encontrei:

• em 1905, Matthew Ryan (desconheço quem foi ou o que fazia ao certo, aliás ) publicou um folheto de 30 páginas Euclid's World-Renowned Parallel Postulate em que mistura o quinto postulado com religião. Este senhor demonstra o quinto postulado recorrendo a linhas em movimento, o que é não é permitido na geometria euclidiana e, portanto, não faz muito sentido. Este autor revela um autêntico pânico perante a ideia de Geometrias Não-Euclidianas e quase anuncia o apocalipse, como se pode depreender das suas palavras de conclusão: 

"1. As loucas Satânicas deduções da Geometria Não-Euclidiana; juntamente com as declarações tolas dos Não-Euclidianos, mostra que a invenção da Geometria "imaginária" ou Não-Euclidiana é bestialmente tola; e, por isso, de natureza a desorientar as mentes, desperdiçar o tempo, e destruir a saúde de milhões de estudantes cada ano.

2. O ensino da Geometria "imaginária" ou Não-Euclidiana em universidades e escolas geraria uma raça de estudantes arrogantes e imbecis, que colocariam a sociedade em perigo através da aplicação de raciocínios "imaginários" e falaciosos aos temas mais importantes, como o governo humano, trabalho e capital, doutrina Cristã, milagres de Cristo, Deus"

(traduzido de Dudley, 1992, p. 158)

•  em 1931, J. Callahan, o presidente de uma universidade nos EUA apresentou uma demonstração do quinto postulado, numa obra que denominou de Euclid or Einstein. Nesta obra, critica os principais matemáticos que desenvolveram as geometrias não euclidianas: Gauss, Bolyai, Lobachevsky, Riemann.... Ou seja, não é uma tentativa ingénua de quem não conhece a longa história deste postulado, mais pelo contrário, é um tentativa de demonstração que tem por objectivo rebater tudo o que já foi descoberto de geometrias não euclidianas. Contudo, este autor utiliza uma definição de linhas paralelas similar à de Possidónio, estando aí o fundamento para a sua demonstração (dizer que rectas paralelas são equidistantes é equivalente a afirmar o quinto postulado). Esta obra está disponível para consulta na internet em http://www.reciprocalsystem.com/euclid/callahan/front.htm. 

***

Pode parecer descabida esta demonstração do quinto postulado tanto tempo depois de ser demonstrado que é impossível fazê-lo, contudo, não posso deixar de notar, que, se esta publicação está online é porque alguém, na actualidade, a achou suficientemente relevante para a publicar. 

Quererá isto dizer que ainda nos dias de hoje, há quem defenda que se pode demonstrar o quinto postulado de Euclides?

Topo