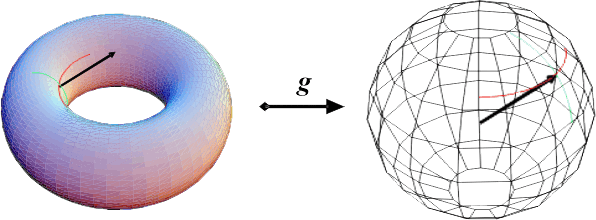
associa a cada ponto $p\in X$ o único vector unitário $g(p)$, perpendicular a $X$ em $p$, que aponta para fora da região limitada por $X$.
Teorema (Gauss-Bonnet)
Sejam $X\subset \mathbb{R}^3$ uma superfície compacta sem bordo,
e $K\colon X\to \mathbb{R}$ a sua curvatura Gaussiana.
$$ \int_X K = 2\pi \, \chi(X) . $$
A aplicação de Gauss $g\colon X\to \mathbb{S}^2$
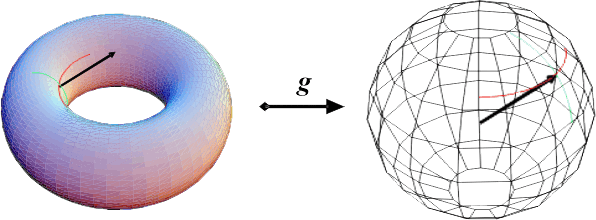
associa a cada ponto $p\in X$ o único vector unitário $g(p)$, perpendicular a $X$ em $p$, que aponta para fora da região limitada por $X$.
$ K(x)= \det( D g_x) \;\; $ e $\;\; {\rm deg}(g)=\frac{1}{2}\,\chi(X) $
$$\Downarrow $$ \begin{align*} \int_X K d{\rm A} & =\int_X \det(D g_x)\, dx = {\rm deg}(g)\,{\rm Area}(\mathbb{S}^2) \\ &= 4\, \pi \, {\rm deg}(g) = 2\,\pi\,\chi(X) . \end{align*}
>> Teoria do Grau