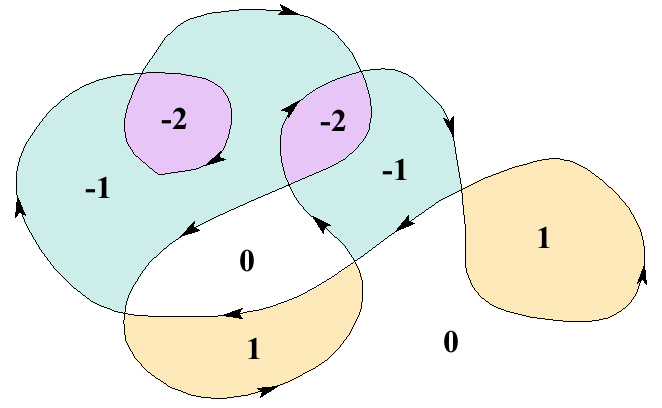
Índice de uma Curva fechada relativo a um Ponto

Dada uma curva fechada $\Gamma$ e um ponto $p\in\Gamma$, o índice de $\Gamma$ relativo a $p$ mede o número de voltas que $\Gamma$ dá em torno de $p$.

Seja $\gamma\colon \mathbb{S}^1\to \mathbb{R}^2$ uma parametrização de $\Gamma$.
O índice define-se por

${\rm Ind}(\Gamma, p) = {\rm deg}(f)$, onde $f\colon \mathbb{S}^1\to \mathbb{S}^1$, $\; f(x)= \frac{\gamma(x)-p}{\| \gamma(x)-p\|}$

     

Proposição
Sejam $\Gamma_1$ e $\Gamma_2$ duas curvas em $\mathbb{R}^2\setminus\{(0,0)\}$.
Se $\Gamma_1$ é homotópica a $\Gamma_2$ então ${\rm Ind}(\Gamma_1,p) = {\rm Ind}(\Gamma_2,p) $.