

$\beta_1 =0$
$\beta_2 =1$


$\beta_1 =2$
$\beta_2 =1$
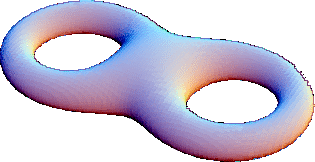

$\beta_1 =4$
$\beta_2 =1$


$\beta_1 =6$
$\beta_2 =1$
$\chi(X) =$ característica de Euler do espaço topológico X
$\beta_i(X,\mathbb{K})=\dim H_i(X,\mathbb{K}) = $ $i$-ésimo número de Betti de $X$ com coeficientes em $\mathbb{K}$
Numa superfície $X$ com uma estrutura de CW-complexo com $V$ vértices, $A$ arestas e $F$ faces$$ \chi(X) = F - A + V . $$
Os números de Betti da tabela seguinte correspondem ao corpo dos números reais.
| Banda de Möbius |  |
 |
$\chi = 0$ |
$\beta_0 =1$ $\beta_1 =1$ $\beta_2 =0$ |
| Garrafa de Klein | 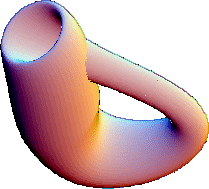 |
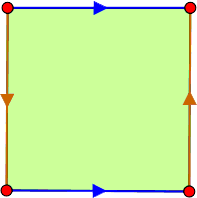 |
$\chi = 0$ |
$\beta_0 =1$ $\beta_1 =1$ $\beta_2 =0$ |
| Plano Projectivo |  |
 |
$\chi = 1$ |
$\beta_0 =1$ $\beta_1 =0$ $\beta_2 =0$ |
| Disco |  |
 |
$\chi = 1$ |
$\beta_0 =1$ $\beta_1 =0$ $\beta_2 =0$ |
| Anel |  |
 |
$\chi = 0$ |
$\beta_0 =1$ $\beta_1 =1$ $\beta_2 =0$ |
| Disco com 2 buracos |  |
 |
$\chi = -1$ |
$\beta_0 =1$ $\beta_1 =2$ $\beta_2 =0$ |
| Disco com 3 buracos |  |
 |
$\chi = -2$ |
$\beta_0 =1$ $\beta_1 =3$ $\beta_2 =0$ |
>> Página Principal