A MÃO - PRIMEIRA “MÁQUINA DE CONTAR”

Multiplicação digital dos números compreendidos entre 10 e 15     

Por um procedimento semelhante podem-se multiplicar entre si números compreendidos entre 10 e 15. Para este procedimento tem ainda de se saber o quadrados perfeitos do número inferior, neste caso o número 10 (10² =100). Assim, por exemplo,

 
Outro exemplo:

Multiplicação digital dos números compreendidos entre 15 e 20 e seguintes

Por técnica semelhante consegue-se multiplicar, entre si, números compreendidos entre 15 e 20, números compreendidos entre 20 e 25 e assim por diante.

Essas técnicas pressupõem o conhecimento de cor dos quadrados perfeitos de 10, 15, 20, 25, ... , e justificam-se pelas fórmulas seguintes:

- Multiplicação dos números compreendidos entre 10 e 15:

10 [(x – 10) + (y – 10)] + (x – 10) (y – 10) + 10² = x.y (fig. 19)

- Multiplicação dos números compreendidos entre 15 e 20:

15 [(x – 15) + (y – 15)] + (x – 15) (y – 15) + 15² = x.y (fig. 20)

- Multiplicação dos números compreendidos entre 20 e 25:

20 [(x – 20) + (y – 20)] + (x – 20) (y – 20) + 20² = x.y

           
Percebe-se assim como, durante vários séculos, os homens graças à sua memória e aos múltiplos recursos dos dedos das suas mãos conseguiam contar e calcular (fig. 21).

Fig. 21- 0 cálculo digital numa pintura funerária egípcia do Novo Império. [Fragmento de uma pintura mural que ornamentava a tumba do príncipe Menna em Tebas, que viveu na época da XVIII dinastia, sob o reino de Tutmosis IV, isto é, no fim do século XV a. C.] Seis escribas contábeis vigiam quatro trabalhadores que medem o grão e enchem vasos de trigo de um monte ao outro; à direita, num dos montes de grãos, o chefe escriba efetua operações aritméticas com os dedos e dita os resultados correspondentes aos três escribas da esquerda, que os registram em tabuletas (isso lhes permitirá, na sequência recopiar seus principais elementos em papiros estocados entre os arquivos do faraó). Tumba tebana n° 69, parede de entrada, 1ª sala à direita.

Como contar com os dedos até dez bilhões

Esta técnica de contagem com os dedos é bem mais completa e matematicamente mais interessante do que todos os sistemas anteriores. Desde o século XVI que se encontra fundamentada e descrita na obra de cálculo publicada em 1593: Suan fa tong zong. Ainda hoje é usada em Cantão e na China.
Considera-se que, cada articulação subjacente a cada falange é subdividida em três partes: junta à esquerda, junta ao centro e junta à direita. Assim, cada dedo fica associado às nove unidades consecutivas de uma mesma ordem decimal: o mínimo direito às unidades simples, o anelar da mesma mão às dezenas, o médio às centenas, o indicador aos milhares e o polegar direito às dezenas de milhar; depois, o polegar esquerdo é associado às centenas de milhar, o indicador da mesma mão aos milhões e assim por diante.

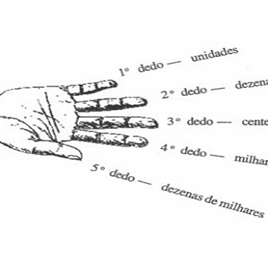(fig. 22)

 No mínimo direito conta-se inicialmente de 1 a 3 ao tocar sucessivamente, do lado esquerdo, as juntas superior, média e inferior. Em seguida, conta-se de 4 a 6 tocando sucessivamente, do lado central, e de baixo para cima, as articulações inferior, média e superior. Por fim, conta-se de 7 a 9, ao considerar-se do lado esquerdo e de cima para baixo, as juntas superior, média e inferior.

Se procedermos de igual forma sobre o dedo anelar direito conta-se inicialmente de 10 a 30, depois de 40 a 60 e por fim de 70 a 90.
Ao usar o médio direito pode-se contar de 100 a 900 e assim por diante até que na articulação inferior direita do mínimo esquerdo se atinge nove milhões.

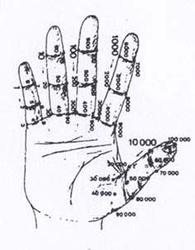
(fig. 23)

A técnica descrita permite, pelo menos em teoria, contar até cem mil numa mão e até dez bilhões nas duas.

É um belo testemunho da engenhosidade do espírito humano…

Para Trás «««