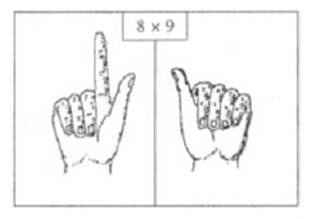
(fig. 15)
8 x 9 = (3 x 4) x 10 + 2 x 1 = 72
A MÃO -
PRIMEIRA
“MÁQUINA DE CONTAR”
Como calcular com os dedos
No
âmbito desta “informática digital” dos antigos, importa referir que a mão do
homem não serviu apenas para contar mas também para efectuar diversas operações
aritméticas. Ainda hoje, na Índia, Síria, Irão, Sérvia, Bessarábia, Auverne e
África do Norte se encontram individuos capazes de fazre multiplicações apenas
com os dedos.
Por exemplo, para multiplicar 8 por 9, dobram-se numa mão, tantos dedos quantas
as unidades suplementares de oito relativamente a 5, ou seja, 8-5=3 dedos, e
mantêm-se os outros dois dedos estendidos. Na outra mão dobram-se tantos dedos
quantas as unidades suplementares em 9 relativamente a 5, ou seja, 9-5=4 e
mantem-se um dedo estendido. Para obter mentalmente o resultado do produto
multiplica-se por dez o número de dedos dobrados nas duas mãos - o que dá
(3+4)x10=70 – e acrescenta-se a esse resultado o produto do número de dedos
estendidos numa mão pelo número de dedos estendidos na outra mão – 2x1=2. Logo,
o produto é 70+2=72
Em resumo:
|
(fig. 15) |
8 x 9 = (3 x 4) x 10 + 2 x 1 = 72 |
Para mutiplicar 9 por 7:
|
(fig. 16) |
9 x 7 = (4 + 2 ) x 10 + 1 x 3 = 63 |
Este procedimento permite efectuar rapidamente as multiplicações de todos os
números entre 5 e 10. Vejamos dois exemplos:
|
||
|
A justificação matemática
deste procedimento é a seguinte:
Sejam x e y dois números compreendidos enter 5 e 10 que se querem multiplicar
entre si. Dobremos, numa mão, tantos dedos quantas as unidades suplementares em
x relativamente a 5, isto é, (x-5) dedos e, na outra mão, tantos dedos quantas
as unidades suplementares em y relativamente a 5, ou seja, (y-5) dedos. O número
de dedos estendidos na primeira mão é igual a A e o número de dedos estendidos
na segunda mão é igual a B, em que
A = 5 – (x – 5) e B = 5 – (y – 5)
O número rotal de dedos dobrados nas duas mãos, é igual a:
R = (x-5) + (y-5)
A regra que diz respeito a esta multiplicação digital é baseada na expressão
(10 x R) + (A + B)
(produto por dez do número total de dedos dobrados, acrescido do produto do número de dedos estendidos) e corresponde exactamente a:
10[(x – 59 + (y – 5)] + [5 – (x – 5)] x [5 – (y – 5)] = x.y
isto é, o produto procurado.