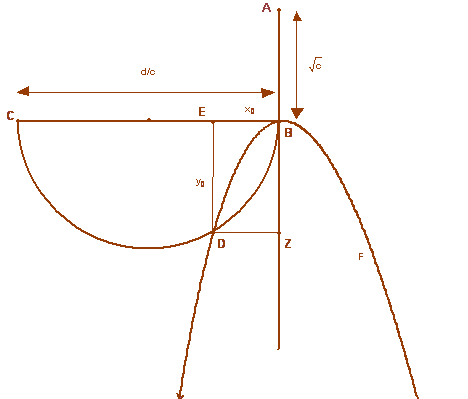A Geometria em Al-Khwārizmī e em al-Khayyām

Na obra Al-Kitāb al-muhtasar fī hisāb al-ğabr wa-l-muqābala (Obra breve sobre a álgebra e almucabala), depois de ter explicado exclusivamente por palavras a resolução das equações do segundo grau, Al-Khwārizmī afirma a necessidade de demonstrar geometricamente os resultados discutidos anteriormente. Relativamente à equação quadrados mais raízes igual a números, escolheu como exemplo x2+10x=39. A completação do quadrado é feita da seguinte forma:
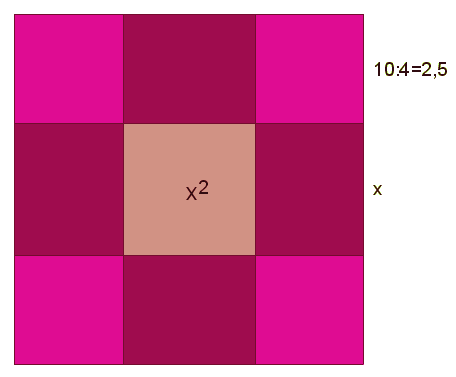 |
a) Lado do quadrado do centro = x b) Lado de cada um dos quadrados dos cantos = 2,5 c) Lado do quadrado maior = x + 2,5 + 2,5 = x + 5 d) Lados do rectângulo: x e 2,5 e) Área do quadrado do centro = x2 f) Área de cada um dos quadrados menores = 2,52 = 6,25 g) Área dos quatro quadrados menores = 4.(6,25) = 25 h) Área do quadrado maior = (x+5)2 i) Área de cada rectângulo = 2,5x j) Área dos quatro rectângulos = 10x |
O primeiro termo da equação é igual a e) + j), donde e) + j) =39. Se a este número somarmos a área dos quatro quadrados dos cantos, g), obtemos 39+25=64. Este número corresponderá então à área do quadrado maior, cujo lado terá de ser a raiz de 64, ou seja 8. Se a este número subtrairmos 2,5 duas vezes, obtemos 3 que será o valor de x.
Outra demonstração da mesma equação é:
 |
a) Lado do quadrado do centro = x b) Lado do quadrado do canto superior = 5 c) Lado do quadrado maior = x + 5 d) Lados do rectângulo: x e 5 e) Área do quadrado do centro = x2 f) Área do quadrado do canto superior = 52 = 25 g) Área do quadrado maior = (x+5)2 h) Área de cada rectângulo = 5x i) Área dos dois rectângulos = 10x |
A área do quadrado original mais a área de dois rectângulos será x2 + 5x + 5x = x2 + 10x, o que será igual a 39, visto ser o primeiro termo da equação. A área do quadrado maior será então 39 + 52 = 39 +25 = 64, logo o lado do quadrado maior é 8 e portanto x terá de ser igual a três.

Al-Khayyām, na resolução da equação cúbica x3 + cx = d, apresenta na Risāla fi-l-barāhīn ‘ala masā’il al-ğabr wa’l-muqābala (Tratado sobre as demonstrações de problemas de al-ğabr e al-mucabala) a seguinte demonstração geométrica, que se encontra explicada em As Obras e os Autores, no subtópico Álgebra, deste site: