A
velha questão: “Quem nasceu primeiro: o ovo ou a galinha?” é o exemplo
mais familiar daquilo a que os matemáticos chamam regressão infinita. Se o ovo
nasceu da galinha que nasceu de um ovo, etc.,
vemo-nos embrenhados num raciocínio que recua no tempo sem que a cada
passo se esteja mais perto do fim do que antes: é infinito.
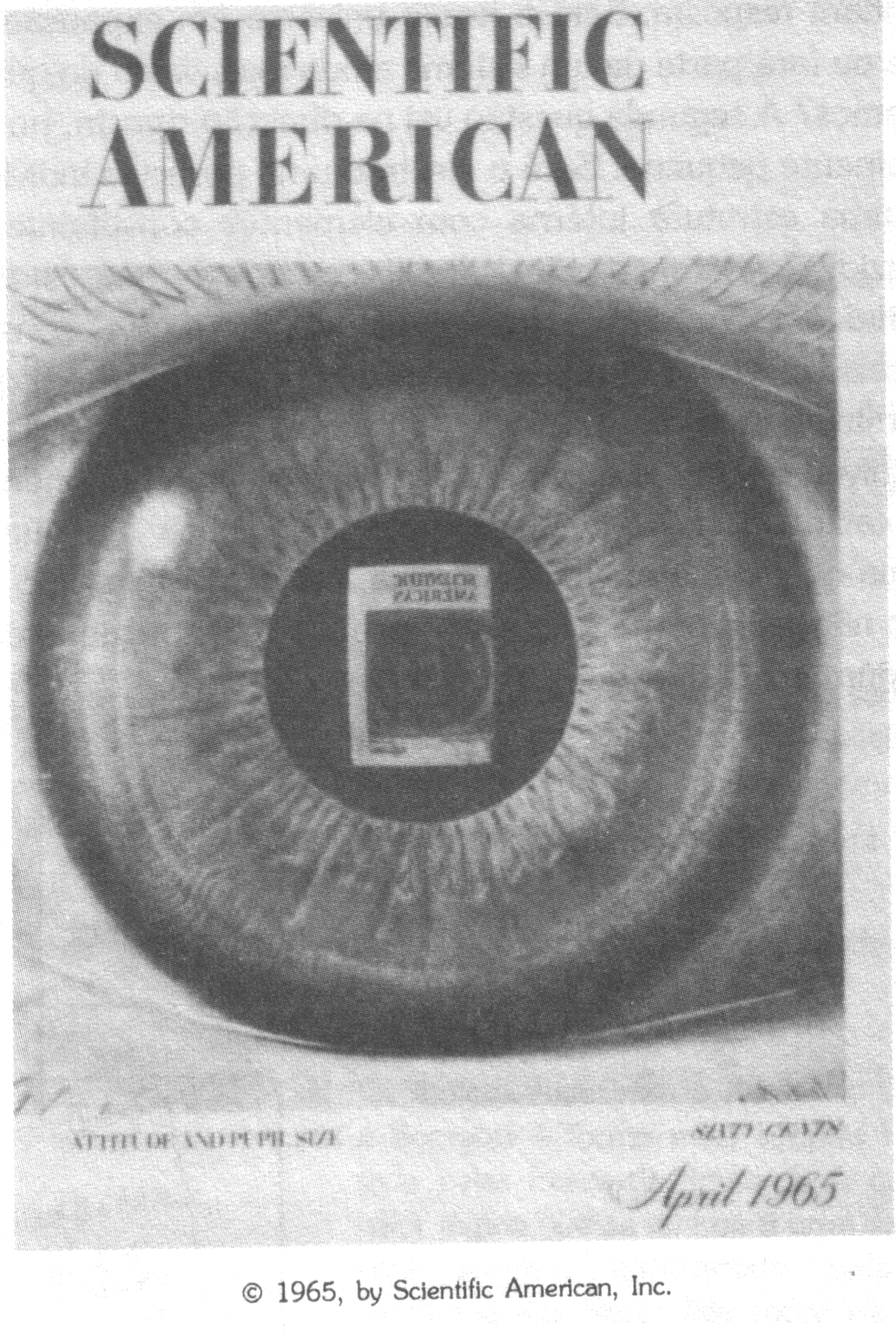
Outro
exemplo é o que podemos observar na figura seguinte; é uma reprodução da
capa da revista Scientific American de Abril de 1965, a qual aparece reflectida
num olho humano. A imagem reflectida, por sua vez, representa um olho mais
pequeno reflectindo uma capa mais pequena, e assim sucessivamente.

Podemos
encontrar também exemplos na literatura, por exemplo Jonathan Swift descreveu
num dos seus poemas uma regressão infinita envolvendo pulgas. Esse poema foi
rescrito pelo matemático Augustos de
Morgan:
|
Pulgas grandes pequenas pulgas têm Sobre as costas para as morderem E as pulgas pequenas mais pequenas pulgas têm, E assim ad infinitum. E as pulgas grandes, por sua vez, Maiores pulgas têm para morderem, Enquanto estas as têm ainda maiores, E essas maiores ainda, e assim sucessivamente.
(Morgan, cit in Gardner, 1993, p. 23) |
Um
paradoxo famoso relacionado com a regressão infinita é o Paradoxo de Platão e
Sócrates.