A TEORIA DE CANTOR

Podemos imaginar pontos distribuídos ordenadamente sobre uma recta ou eixo ordenado. Se todos os racionais forem colocados sobre essa recta será impossível encontrar “buracos” nessa linha: entre dois números, por exemplo 1/2 e 2/3, existe um outro número, 7/12; entre 1/2 e 7/12 existe 13/24, e entre estes existe ainda outro, e assim sucessivamente... Isto é, parecerá que os pontos estão unidos entre si. Na terminologia de Cantor, existe uma correspondência biunívoca entre todos os pontos da linha e todos os números racionais.

Este sistema de números - os racionais - era aquele que Pitágoras acreditava que regia o Universo. No entanto, até Pitágoras sabia que este sistema estava incompleto: há pontos da recta que não estão preenchidos por pontos associados a números racionais, como se pode verificar facilmente marcando sobre ela a hipotenusa de um triângulo rectângulo cujos catetos meçam uma unidade. O ponto determinado pelo comprimento da hipotenusa, Ö2, não tem equivalente numérico no sistema racional de números. Assim, nem todos os pontos da linha estavam efectivamente preenchidos pelo que não há correspondência biunívoca entre todos os pontos e todos os números.

O comprimento da hipotenusa é irracional; para preencher as lacunas na linha, os números irracionais têm de ser introduzidos no sistema. Mas com que fundamento, para além da conveniência e da necessidade, é que eles são introduzidos? E será que a sua admissão resulta no preenchimento de todos os espaços? Foram estas as questões que Cantor se propôs responder, e ao respondê-las transformou radicalmente a ideia acerca daquilo que o número é.

A sua abordagem do problema foi tão simples que a sua solução chegou a ser considerada por muitos como simplesmente ridícula. Cantor começou por contar todos os inteiros, todos os números racionais, e todos os números reais. Obviamente, não pode contar todos os números, porque há um número infinito de cada tipo, mas Cantor não estava interessado em saber exactamente quantos números existem; quis foi descobrir quantos de cada tipo estavam em relação com os de outros tipos. Para isso seguiu o caminho que seguiria qualquer pessoa que não soubesse contar. Se lhe fossem dadas duas caixas com bolas e lhe perguntassem qual tinha mais, ela poderia facilmente descobrir tirando simultaneamente uma bola de cada caixa; se uma caixa ficasse vazia antes da outra, essa caixa tinha menos bolas; se ambas ficassem vazias ao mesmo tempo, elas continham a mesma quantidade de bolas.

Cantor fez a mesma coisa, mas em vez de usar bolas usou números; e em vez de usar caixas usou aquilo a que ele chamou conjuntos ou classes. Um conjunto ou classe é simplesmente uma colecção de coisas semelhantes, podem ser maçãs, bolas, pessoas, linhas, pontos, números, qualquer coisa! Cantor decidiu que os membros dos conjuntos com que trabalharia seriam todos números, tendo uma propriedade em comum. Assim, os membros de um conjunto seriam os números pares, de outro os ímpares, de outro os inteiros, e assim sucessivamente. Cantor procedeu então à comparação do “tamanho” ou cardinalidade destes conjuntos emparelhando os seus elementos. Se cada elemento de um conjunto pudesse ser emparelhado com um único elemento de um outro conjunto, então os conjuntos teriam ambos a mesma cardinalidade.

Tomando o conjunto dos números inteiros, emparelhou os seus elementos com os do conjunto dos números pares, e descobriu que há tantos inteiros quantos os números inteiros pares! Isto pode ser facilmente visto na tabela que se segue.    

Para cada número inteiro há um número par correspondente: o seu dobro. Assim, Cantor chegou à notável conclusão de que, quando estamos a considerar quantidades infinitas, o todo nem sempre é maior do que cada uma das suas partes. Qualquer conjunto infinito cujos membros sejam qualquer subconjunto de números inteiros, têm exactamente a mesma cardinalidade que o conjunto de todos os números inteiros. Por exemplo, há tantos quadrados quantos os números inteiros negativos, há tantos cubos quantos os números divisíveis por 100, há tantos ímpares quantos os múltiplos de 2000, ... existindo tantos elementos nestes subconjuntos considerados como em todo o conjunto dos números inteiros. (Veja-se a tabela abaixo.)   

De facto, Cantor descobriu algo que parece agora bastante óbvio: não existe nenhum conjunto infinito que seja “mais pequeno”, isto é que tenha menor cardinalidade, do que o conjunto dos números inteiros. Para representar o número de elementos existentes neste conjunto, Cantor adoptou o termo aleph zero, que se representa por À₀. Aleph é a primeira letra do alfabeto hebraico. Para distinguir este novo número dos número finitos, ele designou-o como transfinito. No entanto, À₀ é tanto um número como 1 ou como 36, ou qualquer outro número.

De seguida, Cantor questionou-se se existiriam outros números transfinitos, isto é, será que existem conjuntos infinitos cuja cardinalidade seja maior do que a do conjunto dos números inteiros?

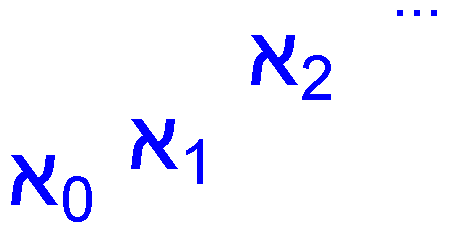
Aparentemente, parecem existir mais números racionais, visto que incluem as fracções, do que números inteiros. No entanto, Cantor emparelhou os elementos dos dois conjuntos e descobriu que tinham a mesma cardinalidade. Há tantas fracções e números inteiros juntos quantos os números inteiros apenas!  

Antes de considerarmos os números reais, que inclui o conjunto dos irracionais, é bom recordar alguma da teoria que Cantor já  tinha à sua disposição na altura.

Em 1844, J. Liouville provou que existem duas categorias de números irracionais: os algébricos e os transcendentes. Um número algébrico é aquele que pode ser raiz de uma equação algébrica; uma vez que existem infinitas equações algébricas, existe também um número infinito de suas raízes, racionais e irracionais. No entanto, há números que nunca podem ser raízes de uma equação algébrica; por exemplo, é impossível formular uma equação que tenha Π como raiz, porque este número só surge através do uso de processos infinitos de análise, nunca através de processos algébricos finitos. As equações não algébricas como por exemplo exponenciais, logarítmicas ou trigonométricas não têm, por regra, raízes que sejam números algébricos. Os números não algébricos denominam-se transcendentes, e os seus representantes mais conhecidos são Π e e.

Abaixo podemos ver uma representação esquemática do conjunto dos números reais.  

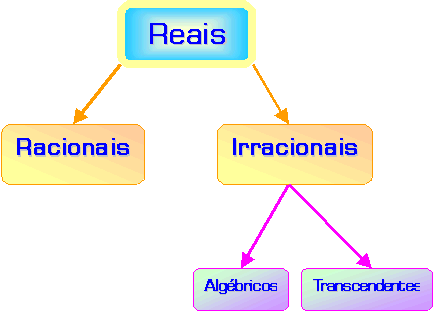
Para comparar a cardinalidade do conjunto dos números inteiros com a dos números reais, Cantor fez a distinção entre os números algébricos e o mais abrangente conjunto dos reais, que comporta também os transcendentes. Primeiro tentou emparelhar os inteiros com os algébricos. Através de um engenhoso método de ordenação das equações algébricas com base nos expoentes dos seus coeficientes, Cantor conseguiu mostrar que as suas raízes, isto é, os números algébricos, podiam ser emparelhados com os números inteiros. Portanto, o conjunto dos números algébricos tem a mesma cardinalidade do dos inteiros.  

Até aqui a procura de um infinito de dimensão superior ao dos inteiros parecia não conduzir a lado nenhum. Todos os conjuntos pareciam ter a mesma cardinalidade, mas Cantor surpreendeu toda a gente - e a si próprio - quando tentou emparelhar o conjunto dos números reais com o dos inteiros e descobriu que era maior, aliás, muito maior! A cardinalidade superior do conjunto dos reais deve-se aos números transcendentes que contém. Quando foram descobertos, pensava-se que estes números eram raros, mas Cantor provou exactamente o contrário: não só eles são comuns, como existem em muito maior quantidade do que qualquer outra espécie de números.

A sua demonstração de que o conjunto dos números reais é “maior” do que o dos inteiros (ou que o dos racionais e até mesmo dos algébricos) é muito simples.  

Primeiro, Cantor admitiu que existia uma correspondência perfeita entre todos os inteiros e todos os números reais de 0 a 1. (Se existir uma correspondência entre todos os inteiros e todos os reais de 0 a 1, existirá também uma correspondência entre todos os inteiros e todos os reais positivos). Para fazer esta correspondência, é preciso listar todos os números reais. Cantor assumiu que esta listagem podia ser feita, escrevendo todos esses números sob a forma de dízimas infinitas, como por exemplo:

Depois, através de um processo de diagonalização, mostrou que esta lista não contém todos os números reais, isto é, por mais exaustiva que seja a nossa lista, há sempre números reais em falta. Por exemplo, um número real diferente de todos os listados pode ser formado do seguinte modo: escolhendo para primeiro dígito um qualquer diferente do primeiro dígito do primeiro número listado, para segundo dígito um qualquer diferente do segundo dígito do segundo número listado, para terceiro um que seja diferente do terceiro dígito do terceiro número listado, e assim sucessivamente. O número resultante terá de ser diferente de todos os que estão na lista porque difere de cada um deles em pelo menos um dígito - o que significa que ele próprio não está na lista. Assim sendo, a suposição de que todos os números reais podiam ser listados e portanto emparelhados com os inteiros está errada, porque conduz a uma contradição.  

Desta forma Cantor provou que o conjunto dos números reais é “maior” do que o conjunto dos números inteiros. Mais, o processo de diagonalização pode ser usado para provar que é sempre possível encontrar conjuntos maiores e maiores - que não existe o conjunto infinito maior de todos. Assim, os números transfinitos (ou ordens de infinito), tal como os números finitos usuais, são infinitos. Cantor chamou a este segundo número transfinito - aquele que representa a cardinalidade dos números reais - C. Ainda não se conseguiu provar se C é mesmo o número transfinito a seguir a À₀, ou se existem outros números transfinitos entre eles. Sabe-se, no entanto, que existem números transfinitos maiores do que C.    

 A teoria de Cantor sobre o infinito está na base da sua teoria dos irracionais, que pela primeira vez fundamentou logicamente os números irracionais e os relacionou com o sistema dos números racionais. Weierstrass, que foi professor de Cantor na Universidade de Berlim, trabalhou também nesta teoria, merecendo talvez mais do que Cantor os méritos da sua criação.  

Ao trabalhar com o infinito, os pré-cantorianos tinham-no considerado como algo nunca alcançado, uma atitude que tinha sido em parte adquirida desde os Gregos.  

Gauss marcou perfeitamente a sua posição quando disse:  

Cantor, no entanto, fez uma distinção entre o infinito potencial e o infinito actual:  

Esta distinção é muito importante: o infinito potencial consiste num processo através do qual um número cresce para além dos limites finitos; o infinito actual não é um processo, é ele próprio um número.  

A distinção entre potencial e actual foi aplicada por Cantor aos números irracionais, e por fim, a todos os números finitos. Segundo ele, qualquer número finito pode ser visto como um processo infinito, com uma espécie de evolução, ou como uma constante fixa, que representa o processo completo. A segunda visão apresentada é a tradicional. No entanto, nenhuma das visões é nova. A primeira, mas não a segunda, é tradicionalmente utilizada quando se trabalha com o infinito; a segunda, mas não a primeira, é tradicionalmente utilizada quando se trabalha com os números racionais; e uma vaga combinação de ambas quando se trabalha com os números irracionais. Cantor unificou as visões, mostrando que todos os números, finitos e transfinitos, podem ser vistos de ambas as formas.  

As duas visões do infinito são, então as seguintes:

O infinito é um limite que nunca se atinge, de um número infinito de números. Isto é, os números 1, 2, 3, 4, 5, ... podem continuar indefinidamente, mas nunca atingirão o último, no infinito. Visto desta maneira, cada número da sequência é apenas um passo de um processo infinito. No entanto, o limite nunca atingido pode ser visto como um número em si mesmo, um número transfinito. Este número transfinito é infinitamente actualizado, é o limite para o qual se tende mas que nunca se atinge, é aquilo que Cantor considera a “quantidade, fixa, constante, para além de todas as quantidades finitas.”  

Da mesma forma, os números irracionais podem ser vistos como o limite de uma sequência infinita de números. Uma sequência de números que tem o infinito como limite é fácil de visualizar, é a sequência dos inteiros, 1, 2, 3, 4, 5, ..., ou pode ser qualquer sequência gerada a partir desta, como por exemplo 1, 2, 4, 8, 16,  ..., em que cada número da sequência é o dobro do antecessor. Como vimos anteriormente, todas estas sequências têm o mesmo “tamanho”, À₀, o primeiro número da sequência dos números transfinitos. O problema agora é como representar as sequências infinitas que têm números irracionais como limite. Também aqui, Cantor resolveu o problema de uma forma tão simples que a maior parte das pessoas nem se lembraria de tentar. Por exemplo, o número irracional Ö2 pode escrever-se na forma de dízima infinita não periódica, 1,414214... Como é que esta dízima pode ser representada por uma sequência infinita de números racionais que se aproximem crescentemente de Ö2 mas que nunca ultrapassem o seu valor?

Isso pode ser feito de forma muito simples:  

1.4, 1.41, 1.414, 1.4142, 1.41421, 1.414214, ... Cada número desta sequência é apenas um passo do processo infinito de geração do número irracional Ö2. Assim, Ö2 é o limite de um processo infinito e, tal como o limite da sucessão dos inteiros pode ser visto como um número, o número transfinito À₀, também o limite da sequência racional 1.4, 1.41, 1.414, 1.4142, 1.41421, 1.414214, ... pode ser visto como um número, o número irracional Ö2. Este número irracional fica assim definido, pela primeira vez na história, apenas em termos de números racionais.  

Nenhum destes dois pontos de vista se aplicam apenas aos números irracionais ou transfinitos. Eles aplicam-se também aos números racionais. Como a visão de um número racional como uma quantidade fixa é suficientemente bem conhecida, será omitida; um número racional visto como limite de um processo infinito é que é menos conhecido e merece ser considerado.  

Todos os números racionais podem ser escritos na forma de dízima infinita. Por exemplo, 4 pode ser escrito como 4.0000..., com os zeros a continuar indefinidamente; a fracção 1/3 é 0.3333..., e 1/7 é 0.1428571428571... Qualquer dízima infinita pode, naturalmente, ser rescrita como uma sequência infinita; e uma sequência infinita deste tipo chegará, depois de um número infinito de passos, ao seu limite. Assim, os números racionais podem também ser vistos como o limite de um processo infinito. Vistos desta perspectiva, eles parecem não diferir dos irracionais - no entanto a diferença existe. Sempre que um número racional é escrito sob a forma de dízima a sua sequência de dígitos repete-se, sendo por esse motivo designados por dízimas infinitas periódicas. No primeiro exemplo que se viu, 0 repetia-se infinitamente, no segundo era 3, e no terceiro era a sequência 142857. As dízimas periódicas são características de todos os racionais e nunca ocorrem nos irracionais. Isto pode ver-se facilmente tomando a dízima 0.142857142857... e pondo x=0.142857... (Note-se que qualquer operação efectuada em ambos os membros da equação, não afectará o valor de x.) Multiplicando ambos os membros da equação por um milhão: 1000000x=142857.142857... Agora subtraindo a primeira equação da segunda:

Esta equação pode agora ser escrita sob a forma de fracção:  

x = 142857/999999. Simplificando a equação vamos obter 1/7. Assim, 1/7 é o equivalente, em termos fraccionários, à dizima infinita periódica 0,142857142857...  

Um número irracional nunca pode ser escrito sob a forma de uma fracção racional e portanto (como podemos concluir invertendo o processo anterior) nunca pode ter uma dízima periódica.  

Estas duas formas de olhar para os números resolveram muitos dos antigos problemas da Matemática, incluindo os dos infinitésimos. Infinitésimos são sucessões que normalmente têm o zero como limite (ao invés de infinito), sendo que a sucessão decresce por quantidades cada vez menores, em vez de crescer. Em ambos os casos, no entanto, as sequências convergem dentro de limites.