Demonstração
Aqui está um comentário do editor sobre as ideias subjacentes à demonstração da suposição que Arquimedes faz na hipótese 4:
Até agora a carta foi literalmente traduzida devido ao interesse histórico inerente ao ipsissima verba de Arquimedes em tal assunto. O restante trabalho pode agora ser mais livremente reproduzido, e, antes de proceder com os conteúdos matemáticos, só é necessário comentar que Arquimedes a seguir descreve como ele chegou a um limite superior e inferior para o ângulo subtendente pelo sol. Ele fez isto pegando numa vara grande ou régua, atando um pequeno cilindro ou disco na ponta, e apontando a vara na direcção do sol logo ao nascer deste (para que seja possível olhar para o sol directamente), depois pondo o cilindro a uma distância de tal forma que ocultasse e que quase oculta, o sol, e por fim medindo os ângulos subtendentes pelo cilindro.
Ele explica também a correcção que ele achou necessária fazer porque "o olho não vê de um dado ponto mas sim de uma dada área".
O resultado da experiência tinha como propósito mostrar que o ângulo
subtendente pelo diâmetro do sol era menor do que
-ésima parte, e maior do
que
-ésima
parte, de um ângulo recto.
Para provar que o diâmetro do sol é maior do que o lado de um polígono com 1000 lados iguais inscrito no círculo maior do 'universo'.
Suponha-se que o plano do papel é o plano que passa pelo centro do sol, o centro da terra e do olho, à hora em que o sol tenha acabado de nascer acima do horizonte. Consideremos o círculo EHL resultante da intersecção do plano com a terra e o círculo FKG resultante da intersecção do plano com o sol, sendo C e O o centro da terra e do sol respectivamente, e sendo E a posição do olho.
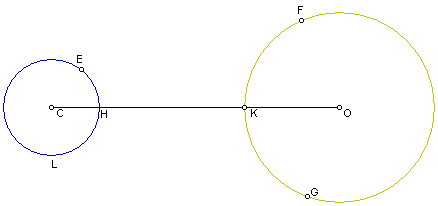
Consideremos ainda, o círculo maior AOB resultante da intersecção do plano com a esfera do 'universo' (isto é, a esfera cujo centro é C e cujo raio é CO).
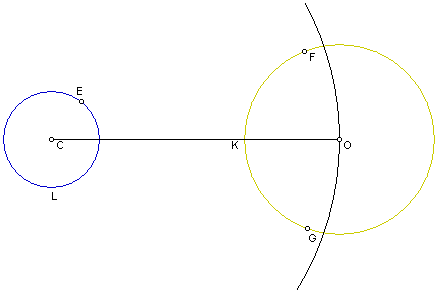
Desenhe-se duas tangentes ao circulo FKG com ponto de intersecção E, e que passam pelos pontos P,Q e a partir de C desenhe-se outras duas tangentes ao mesmo círculo passando pelos pontos F e G respectivamente.
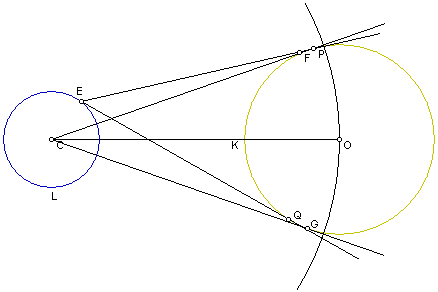
Seja CO o segmento de recta que intersecta o sol no ponto H e a terra no ponto K; e sejam CF, CG os segmentos de recta que passam pelos pontos A e B respectivamente no círculo maior AOB.
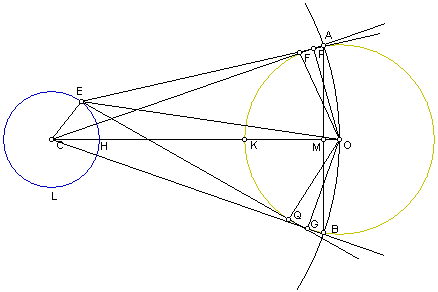
Trace-se os segmentos EO, OF, OG, OP, OQ, AB, e seja AB o segmento de recta de tal forma que o segmento CO intersecte AB no ponto M.
Assim CO>EO, pois o sol está acima do horizonte.
Portanto Ð PEQ > Ð FCG.
E
Ð
PEQ
>
R
Mas
<
R , onde R representa um ângulo recto.
Logo Ð
FCG <
R, a
fortiori,
e o arco do círculo maior associado à corda AB é
menor do que 
-ésima parte da circunferência deste círculo, isto é
AB < (lado de um polígono com 656 lados inscrito no círculo).
Ora o perímetro de qualquer polígono inscrito no círculo maior é menor do
que
CO. [Cf. Medida de um círculo, Prop.3.]
Portanto AB : CO < 11 : 1148,
e
a fortiori, AB <
CO..............................(a)
.
Assim, uma vez que CA = CO, e AM é perpendicular a CO, enquanto que OF é perpendicular a CA, vem AM = OF.
Portanto AB = 2AM = (diâmetro do sol).
Desta forma
(diâmetro do sol) <
CO, por (a)
,
e, a fortiori,
(diâmetro da terra) <
CO. [Suposição2]
Por isso
CH + OK <
CO,
assim
HK >
CO,
ou CO : HK < 100 : 99.
E CO > CF,
por outro lado HK < EQ.
Portanto CF : EQ < 100 : 99..............................(ß).
Consideremos agora o lado adjacente ao ângulo recto dos triângulos rectos CFO, EQO respectivamente,
OF = OQ, mas EQ < CF (pois EO < CO).
Portanto Ð OEQ : Ð OCF > CO : EO,
mas < CF : EQ *
|
*A proposição aqui suposta é claro equivalente à fórmula trigonométrica que afirma que, se a , ß são o comprimento de arco de dois ângulos, cada um menor do que um ângulo recto, do qual a é maior, então
|
(nota do editor).
Multiplicando os ângulos por 2, Ð PEQ : Ð ACB < CF : EQ
< 100 : 99, por (ß).
Mas Ð
PEQ >
R, por hipótese.
Portanto
Ð ACB >
R
>
R.
Sai então que o arco AB é maior do que
-ésima parte da circunferência do
círculo maior AOB.
Logo, a fortiori, AB > (lado de um polígono com 1000 lados inscrito no círculo maior),
e AB é igual ao diâmetro do sol, como queríamos demonstrar.
_________________________________________________________
Os seguintes resultados podem agora ser demonstrados:
(diâmetro do 'universo') < 10.000 (diâmetro da terra);
e (diâmetro do 'universo') < 10.000.000.000 estádios.
(1) Suponha-se, para simplificar a notação, que
representa o diâmetro do
'universo',
o diâmetro do sol,
o
diâmetro da terra, e
o diâmetro da lua.
Por hipótese, 
não é > 30
[Suposição 3]
e
>
; [ Suposição 2]
logo
< 30
.
Por outro lado, pela última proposição,
> (lado de um polígono regular com 1000 lados inscrito no círculo maior),
assim
(perímetro de um polígono regular com 1000 lados) < 1000
< 30.000
.
Mas o perímetro de qualquer polígono regular com mais de seis lados inscrito num círculo é maior do que um hexágono regular inscrito nesse mesmo círculo, e portanto maior do que 3 vezes o diâmetro.
Assim,
(perímetro
de um polígono regular com 1000 lados) >
3
.
Consequentemente
< 10.000
.
(2) (Perímetro da terra) não é > 3.000.000 estádios.
[Suposição 1]
e
(perímetro da terra) > 3
.
Portanto
< 1.000.000 estádios,
donde
< 10.000.000.000 estádios.
_________________________________________________________
