"Há quem pense, Rei Gelão, que o número de grãos de areia é infinito. E quando menciono areia refiro-me não só aquela que existe em Siracusa e no resto da Sicilia mas também àquela que se encontra nas outras regiões, sejam elas habitadas ou desabitadas. Mais uma vez, há quem, sem considerá-lo infinito, pense que nenhum número foi ainda nomeado que seja suficientemente grande para exceder a sua multiplicidade. E é claro que aqueles que têm esta opinião, se imaginassem uma massa de areia tão grande como a massa da terra, incluindo nesta todos os mares e depressões da terra preenchidas até uma altura igual à mais alta das montanhas, estariam muito longe ainda de reconhecer que qualquer número poderia ser expresso de tal forma que excedesse a multiplicidade da areia aí existente. Mas eu tentarei mostrar-vos, através de provas geométricas que conseguireis acompanhar que, dos números nomeados por mim e que constam no trabalho que enviei a Zeuxipo, alguns excedem, não só o número da massa de areia igual em magnitude à da terra preenchida da maneira que atrás referi, mas também da massa igual em magnitude à do universo. Ora, vós estais por certo conscientes de que 'universo' é o nome dado por muitos astrónomos à esfera cujo centro é o centro da terra e cujo raio é igual à linha recta entre o centro do sol e o centro da terra. Esta é a definição comum, como tendes ouvido dos astrónomos. Mas Aristarco de Samos escreveu um livro no qual as premissas levam ao resultado de que o universo é muitas vezes maior do que aquele que é agora considerado. A hipótese dele é que as estrelas fixas e o sol permanecem imóveis, que a terra gira em torno do sol na forma de uma circunferência, que o sol permanece no centro da órbita e que a esfera das estrelas fixas, situada relativamente perto do centro do sol, é tão grande que o círculo em que ele supõe que a terra gira suporta uma proporção, relativamente à distância das estrelas fixas tal como o centro da esfera suporta relativamente à sua superfície. É fácil de ver que isto é impossível; pois dado que o centro da esfera não tem dimensão, não o podemos conceber para suportar qualquer proporção relativamente à superfície da esfera. Temos contudo de aceitar que Aristarco assim pense pela nossa parte, porque consideramos a terra como se fosse o centro do universo, a proporção que a terra suporta relativamente àquilo que descrevemos como sendo o 'universo' é igual  à proporção da esfera contendo o círculo em que ele supõe que a terra gira comparativamente à esfera das estrelas fixas. Pois ele faz uma adaptação dos seus resultados às demonstrações tendo em conta hipóteses deste tipo, e em particular parece que ele supõe que a magnitude da esfera que representa a terra em movimento é igual à magnitude daquilo a que chamamos o 'universo'. Então eu digo que, mesmo que uma esfera constituída por uma tão elevada quantidade de areia como sendo comparativa à da esfera das estrelas fixas, como supõe Aristarco, eu continuarei a demonstrar que, dos números mencionados nos "Princípios", alguns excedem em multiplicidade o número da areia igual em magnitude à esfera atrás referida, desde que as seguintes suposições sejam feitas.

1. O perímetro da terra é de cerca de 3.000.000 estádios e não é maior que este número.

É verdade que como de certo sabeis, alguns já tentaram demonstrar que o tal perímetro é de cerca de 300.000 estádios. Mas eu vou mais longe e, considerando a magnitude da terra dez vezes o tamanho que os meus antecessores pensaram, suponho que o seu perímetro é de cerca de 3.000.000 estádios e não é mais.

2. O diâmetro da terra é maior do que o diâmetro da lua, e o diâmetro do sol é maior do que o diâmetro da terra.  

Com esta suposição eu sou da opinião dos primeiros astrónomos.

3. O diâmetro do sol é cerca de 30 vezes o diâmetro da lua e não é maior. 

É verdade que, entre os primeiros astrónomos, Eudoxus (408-355 B.C.) declarou ser o diâmetro do sol cerca de nove vezes maior do que o da lua, e Pheidias (500-432 B.C.) doze vezes maior, enquanto que Aristarco tentou provar que o diâmetro do sol é maior 18 vezes, mas menor do que 20 vezes o da lua. Mas eu vou mais além de Aristarco para que a veracidade da minha proposição possa ser estabelecida para além de todas as disputas, e suponho que o diâmetro do sol é cerca de 30 vezes o da lua e não é maior.

4. O diâmetro do sol é maior do que o lado do polígono regular com 1000 lados inscrito no maior círculo (na esfera) do universo.

Faço esta suposição porque Aristarco descobriu que o sol pareceu ser cerca de 1/720-ésima parte do círculo do zodíaco, e eu próprio, por um método que em seguida vou descrever, tentei descobrir experimentalmente o ângulo subtendente pelo sol e tendo o seu vértice no olho."  

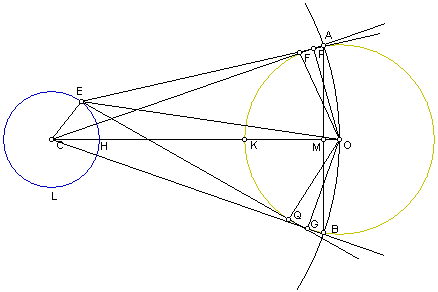
O resultado da experiência tinha como propósito mostrar que o ângulo subtendente pelo diâmetro do sol era menor do que 1/164-ésima parte, e maior do que 1/200-ésima parte, de um ângulo recto.

Para provar que o diâmetro do sol é maior do que o lado de um polígono com 1000 lados iguais inscrito no círculo maior do 'universo'. 

Suponha-se que o plano do papel é o plano que passa pelo centro do sol, o centro da terra e do olho, à hora em que o sol tenha acabado de nascer acima do horizonte. Consideremos o círculo EHL resultante da intersecção do plano com a terra e o círculo FKG resultante da intersecção do plano com o sol, sendo C e O o centro da terra e do sol respectivamente, e sendo E a posição do olho.

Consideremos ainda o círculo maior AOB resultante da intersecção do plano com a esfera do 'universo' (isto é, a esfera cujo centro é C e cujo raio é CO).

Desenhem-se duas tangentes ao circulo FKG com ponto de intersecção E, e que passe pelos pontos P,Q e a partir de C desenhem-se outras duas tangentes ao mesmo círculo passando pelos pontos F e G respectivamente.

Seja CO o segmento de recta que intersecta o sol no ponto H e a terra no ponto K; e sejam CF, CG os segmentos de recta que passam pelos pontos A e B respectivamente no círculo maior AOB.

Trace-se os segmentos EO, OF, OG, OP, OQ, AB, e seja AB o segmento de recta de tal forma que o segmento CO intersecte AB no ponto M.

Assim CO>EO, pois o sol está acima do horizonte. 

Portanto    Ð PEQ > Ð FCG.

E    Ð PEQ > (1/200)R

Mas            < (1/164)R , onde R representa um ângulo recto.

Logo   Ð FCG < (1/164)R, a fortiori,

e o arco do círculo maior associado à corda AB é menor do que 1/656-ésima parte da circunferência deste círculo, isto é

AB < (lado de um polígono com 656 lados inscrito no círculo).

Ora o perímetro de qualquer polígono inscrito no círculo maior é menor do que (44/7)CO. [Cf. Medida de um círculo, Prop.3.]

Portanto    AB : CO < 11 : 1148,

e a fortiori,    AB < (1/100)CO..............................(a) .

Assim, uma vez que CA = CO, e AM é perpendicular a CO, enquanto que OF é perpendicular a CA, vem    AM = OF.

Portanto    AB = 2AM = (diâmetro do sol).

Desta forma    (diâmetro do sol) < (1/100)CO, por (a) ,

e, a fortiori,    (diâmetro da terra) < (1/100)CO. [Suposição2]

Por isso    CH + OK < (1/100)CO,

assim    HK > (99/100)CO,

ou    CO : HK < 100 : 99.

E    CO > CF,

por outro lado    HK < EQ.

Portanto    CF : EQ < 100 : 99..............................(ß).

Consideremos agora o lado adjacente ao ângulo recto dos triângulos rectos CFO, EQO respectivamente, 

OF = OQ, mas EQ < CF (pois EO < CO).

Portanto    Ð OEQ : Ð OCF > CO : EO,

mas                                        < CF : EQ ².

Multiplicando os ângulos por 2,    РPEQ : Ð ACB < CF : EQ

                                                                                < 100 : 99, por (ß).

Mas    Ð PEQ > (1/200)R, por hipótese.

Portanto    РACB > (99/20000)R

                                > (1/203)R.

Sai então que o arco AB é maior do que 1/812-ésima parte da circunferência do círculo maior AOB.

Logo, a fortiori,    AB > (lado de um polígono com 1000 lados inscrito no círculo maior),

e AB é igual ao diâmetro do sol, como queríamos demonstrar.

________________________________________________________

Os seguintes resultados podem agora ser demonstrados:

    (diâmetro do 'universo') < 10.000 (diâmetro da terra);

e  (diâmetro do 'universo') < 10.000.000.000 estádios.  

   
  (1) Suponha-se, para simplificar a notação, que representa o diâmetro do 'universo', o diâmetro do sol, o diâmetro da terra, e o diâmetro da lua.

Por hipótese,     não é > 30 [Suposição 3]

e    > ; [ Suposição 2]

logo    < 30 .

Por outro lado, pela última proposição,

     > (lado de um polígono regular com 1000 lados inscrito no círculo maior),

assim    (perímetro de um polígono regular com 1000 lados) < 1000

                                                                                            < 30.000 .

Mas o perímetro de qualquer polígono regular com mais de seis lados inscrito num círculo é maior do que um hexágono regular inscrito nesse mesmo círculo, e portanto maior do que 3 vezes o diâmetro. 

Assim,    (perímetro de um polígono regular com 1000 lados) > 3 .

Consequentemente    < 10.000 .

    (2) (Perímetro da terra) não é > 3.000.000 estádios.

[Suposição 1] 

e    (perímetro da terra) > 3 .

Portanto     < 1.000.000 estádios,

donde    < 10.000.000.000 estádios.

_________________________________________________________

Suposição5.

Suponha-se uma dada quantidade de areia não maior do que uma semente de papoila, e suponha-se que não contém mais do que 10.000 grãos.

Suponha-se de seguida que o diâmetro da semente de papoila não é menor do que 40 avos da largura de um dedo.

Ordens e períodos de números

I. Temos nomes tradicionais para números até uma miríade (10.000); podemos portanto expressar números até à miríade miríade (100.000.000). Chamemos a estes números, números de primeira ordem.
Suponha-se que 100.000.000 é a unidade de segunda ordem, e seja a segunda ordem constituída pelos números dessa unidade até (100.000.000)².
Seja então esta a unidade da terceira ordem dos números terminando com (100.000.000)³ e assim sucessivamente, até chegarmos à ordem 100.000.000 dos números terminando com , a que chamaremos P.

II. Suponhamos que os números de 1 a P da forma atrás descrita formam o primeiro período.
Seja P a unidade da primeira ordem do segundo período, e sejam estes constituídos pelos números de P até 100.000.000 P.
Seja o último número a unidade da segunda ordem do segundo período, e que este termine com (100.000.000)² P. 
Podemos proceder deste modo até atingirmos a ordem 100.000.000 do segundo período terminando com P, ou P². 

III. Tomando P² como sendo a unidade da primeira ordem do terceiro período, procedemos da mesma forma até chegarmos à ordem 100.000.000 do terceiro período terminando com P³.

IV. Tomando P³ como sendo a unidade da primeira ordem do quarto período, continuamos o mesmo processo até chegarmos à 100.000.000-ésima ordem do 100.000.000-ésimo período terminando com .  

Octavalentes

Considere a série de termos em proporção contínua em que o primeiro termo é 1 e o segundo é 10. O primeiro termo dos oito primeiros termos da série estão de acordo com a primeira ordem do primeiro período como acima foi descrito, o segundo termo dos oito primeiros termos da série estão de acordo com a segunda ordem do primeiro período, o primeiro termo dos oito primeiros termos da série tem como unidade a correspondente ordem em cada caso. Analogamente para o terceiro termo dos oito primeiros termos da série, e assim por diante, podemos, da mesma forma, escolher quaisquer outros oito termos consecutivos da série.

Teorema

Se existir qualquer número de termos de uma série numa proporção contínua, digamos onde , e se tomarmos quaisquer dois termos ,  e considerarmos o seu produto, o produto . será um termo na mesma série e estará tão distante de , como de está distante de ; também estará distante de  por um número de termos menor do que a soma do número de termos pelos quais  e  respectivamente estão distantes de .

Tome-se o termo que esteja distante de  pelo mesmo número de termos que  está distante de . Este número de termos é m (o primeiro e último sendo ambos contáveis). Logo o termo a considerar está à distância de m termos de , e é portanto o termo .

Temos portanto de provar que .

Assim, termos que estão igualmente distantes de outros termos numa proporção contínua são proporcionais.

Logo .

Mas , pois .

Portanto .

O segundo resultado é agora óbvio, pois  está à distância de m termos de ,  está à distância de n termos de  e  está à distância de (m + n - 1) termos de .

Aplicação ao número da areia

Pela suposição 5,

(diâmetro da semente de papoila) não é < 1/40 (largura de um dedo);

e, como uma esfera está para a outra com razão tripla dos seus diâmetros, segue-se que

Acrescentamos agora gradualmente o diâmetro da esfera em questão, multiplicando-o por 100 de cada vez. Assim, lembrando que a esfera irá ser multiplicada por 100³ ou 1.000.000, o número de grãos de areia que estaria contido numa esfera com cada diâmetro sucessivo pode ser determinado como a seguir se segue.

Mas, pelo teorema, 

     (diâmetro do 'universo') < 10.000.000.000 estádios

Assim o número de grãos de areia contidos numa esfera do tamanho do nosso 'universo' é menor do que 1.000 unidade da sétima ordem dos números.

Disto podemos provar ainda que uma esfera do tamanho atribuído por Aristarcos como sendo a esfera das estrelas fixas conteria um número de grãos de areia menor do que 10.000.000 unidades da oitava ordem.

Pois, por hipótese,

     (terra) : ('universo') = ('universo') : (esfera das estrelas fixas).

E,

     (diâmetro do 'universo') < 10.000 (diâmetro da terra)

bem como

     (diâmetro da esfera das estrelas fixas) < 10.000 (diâmetro do 'universo')

logo

     (esfera das estrelas fixas)< (10.000)³ . ('universo').

Segue-se que o número de grãos de areia que estaria contido numa esfera igual à esfera das estrelas fixas

< (10.000)³ x 1.000 unidade da sétima ordem 

< (13º termo da série) x (52º termo da série)

< 64º termo da série 

< 10.000.000 unidades da oitava ordem dos números.

Conclusão

"Creio que estas coisas, Rei Gelão, possam parecer inacreditáveis para a grande maioria das pessoas que não estudam matemática. Mas para aqueles que estão dentro do assunto e que já pensaram na questão das distâncias e tamanhos da terra, do sol, e da lua e do universo inteiro a prova terá algum fundamento. E foi por este motivo que achei que o tema seria apropriado para a vossa consideração."