Soma
dos Recíprocos dos Quadrados Perfeitos
Euler
mostrou o resultado do seguinte somatório
![]() .
.
Enquanto Oldenburg questionou Leibniz (1646-1716), numa carta de 1673, pelo resultado desta soma, à qual ele não lhe deu resposta, Jacques Bernoulli (1654-1705), em 1689, considerou-se incapaz de obter qualquer tipo de resultado. Euler foi o matemático que revelou maior destreza em obter tal resultado.
Começou
por utilizar a série sen z:
sen
z = z – z3/3! + z5/5! – z7/7! + …
Igualando
a série a 0, obtém-se:
0 = z – z3/3! + z5/5!
– z7/7! + …,
e
dividindo tudo por z, vem
0 = 1 – z2/3! + z4/5!
– z6/7! + …
substituindo
z2 por w, sai,
0 = 1 – w/3! + w2/5! - ...
Da
teoria das equações algébricas, sabe-se que, se o termo constante é 1, a
soma dos recíprocos das raízes é o oposto do coeficiente do termo linear –
neste caso 1/3!. Além disso, sabe-se que as raízes da equação (1) são
±p,
±2p,
±3p, ...
e
as raízes da equação em w são
p2, (2p)2,
(3p)2,
...
Logo,
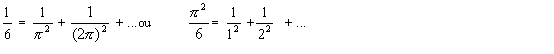
Com
esta despreocupada aplicação Euler conseguiu um resultado que desafiara outros
matemáticos.