Se quiser ter acesso às demonstrações clique em
. De notar, que para as seguir é preciso ter em mente que os números reais
verificam as propriedades de Corpo, vistas na página "O número
imaginário existe realmente?".Números Complexos, uma abordagem científica
Os números complexos apareceram como uma extensão dos números reais.
O seu conjunto representa-se por C e define-se como sendo C = {z = a+ ib: a, b Î R e i2 = -1}, onde R representa o conjunto dos números reais.
Vejamos agora alguns resultados.
Se quiser ter acesso às demonstrações clique em
. De notar, que para as seguir é preciso ter em mente que os números reais
verificam as propriedades de Corpo, vistas na página "O número
imaginário existe realmente?".
Um número complexo representa-se por z =
a + ib com a, b Î
R. Diz-se que:
a é a parte real de z e escreve-se Re(z) = a;
b é a parte imaginária de z e escreve-se Im (z) = b.
Diz-se que:
O complexo z é um número real se e só se Im(z) = 0.
O complexo z é um imaginário puro se e só se Re (z) = 0 e Im(z)
¹
0.
O complexo z é nulo se e só se Re (z) = Im (z) = 0.
Assim,
pode-se definir:
Conjunto dos números reais como R = {a + ib Î
C: b = 0}
Conjunto dos números imaginários puros como I =
{a + ib Î
C: a = 0}
A representação geométrica dos complexos é
feita num referencial cartesiano, em que se fixa o eixo das abcissas
para o conjunto R e o eixo das ordenadas para o conjunto I.
Assim, a cada complexo z = a + ib, corresponde o ponto do plano P(a,
b),
que se designa por afixo de z. Pode-se, também, considerar o
complexo z como o vector OP, sendo O a origem do referencial.
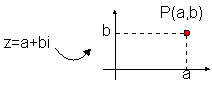
Ao referencial com estas características dá-se o nome de Plano Complexo.
A representação trigonométrica dos números complexos é um caso particular da utilização das coordenadas polares.
Na representação trigonométrica, um número z é determinado pela norma do vector que o representa e pelo ângulo que faz com o semieixo positivo das abcissas.
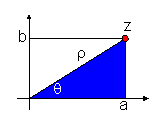
Ao ângulo q
chama-se argumento de z e a r
dá-se o nome de módulo de z, com z = a + ib. Portanto:
q
= arg(z) e
r
= Ö(a2+b2).
Sendo q o argumento de z, q + 2kp também o será. Assim chama-se argumento principal ao q tal que: -p < q £ p
A partir das relações trigonométricas obtêm-se:
cos q = a/r, sen q = b/r Û a = rcos q, b = rsen q. Portanto:
z = a + bi Û z = rcos q + (rsen q)i Û z = r(cos q + i sen q)
A r(cos q +
i sen q) dá-se o nome de cis q
e podemos escrever
z = rcis q.
Da relação tgq = b/a consegue-se o valor de q: é tal que tgq = b/a.
Igualdade de Números Complexos
Dados dois complexos z = a + ib e w = c + id tem-se:
z = w Û a = c Ù b = d
Na forma trigonométrica sendo z = r(cos
q + i sen q) e
w
=
h(cosa
+ isena),
será:
z = w Û rcosq = hcosa Ù rsenq = hsena
O simétrico do número complexo z = a + ib é o número -z = -(a + ib), ou seja -z = (-a) + i(-b).
Corresponde a uma rotação de 180º do afixo de z em torno da origem.
Em
notação trigonométrica, o simétrico de z = rcis
q é -z = r[-cos(-q)
+ isen(-q)].
|
|
Re(-z) = -Re z |
Conjugado de um Número Complexo
O conjugado
do complexo z = a + ib é o número complexo denotado por
z
= a - ib.
Na forma trigonométrica, o conjugado de z = rcis q é z = rcis (-q).
Corresponde a uma reflexão do afixo de z na recta das abcissas.
|
|
Re z
= Re z |
Sendo z = a + bi (¹ 0), o
seu inverso é z -1 = (a - bi)/(a2 +
b2)
Na representação trigonométrica, o inverso de
z = rcis
q é
z -1 = r -1cis(-q).
Quatro Operações com Complexos
Consideremos os números complexos z1
= a + bi e z2 = c + di ou, na forma trigonométrica,
z1 = r1cisq1
e z2 = r2cisq2
Adição
Algebricamente, a soma é na forma: z1 + z2 = a + c + (b + d)i
Na notação trigonométrica não há como simplificar.
De notar que, se z e w forem dois complexos: z + w = w + z.
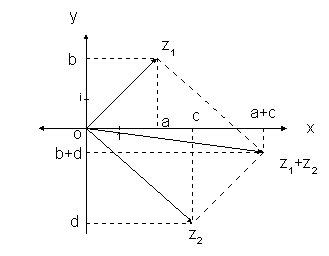
Considerando os números como vectores, geometricamente, a soma de complexos não passa da soma dos vectores que os representam pela "regra do paralelogramo".
Subtracção
A subtracção de z1 por z2
não é mais que a soma de z1 com o simétrico de z2,
ou seja,
z1 - z2 = z1 + (-z2).
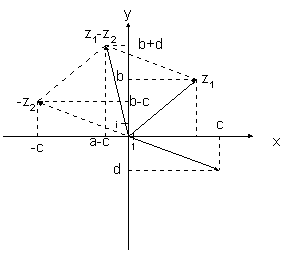
Geometricamente, considerando os números como vectores, a subtracção corresponde à adição do primeiro vector com o simétrico do segundo vector.
O produto de z1 por z2 é o número
complexo
z1.z2 = (ac - bd) + (ad + cb)i
ou, na forma trigonométrica z1.z2
= r1r2cis(q1
+ q2)
Vejamos a interpretação geométrica do produto de dois complexos, z1 = a + ib e z2 = c + id. Esta operação não corresponde, directamente, a nenhuma operação conhecida entre vectores.
Suponhamos que z2 é um número real, isto é, que d = 0; então o produto de z1 por z2 corresponde ao produto do vector (a, b) pelo número real c. Se c>0, então esta operação corresponde a uma dilatação de razão c do vector z1 e se c<0 corresponde a uma dilatação de razão |c| do mesmo vector, seguida de uma rotação de 180º de centro na origem.
Consideremos, agora, que z2 = i. Neste caso o produto do complexo a + bi por i corresponde à rotação de 90º no sentido directo (contrário ao movimento dos ponteiros do relógio) e em torno da origem do vector (a, b), obtendo-se o vector (-b, a).
O produto de um complexo a + bi por um imaginário puro ki combina as duas operações anteriores: o produto do vector (a, b) por k, seguido de uma rotação de 90º no sentido directo em torno da origem do vector obtido.
Estas operações podem ser facilmente visualizadas na figura seguinte:
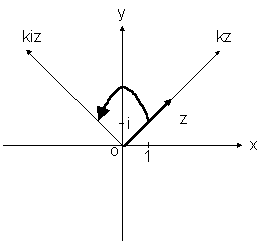
Vejamos agora o produto de um complexo a + bi pelo complexo c + di. Este produto é equivalente a c ´ (a + bi) + di ´ (a + bi), por isso vectorialmente corresponde a:
|
|
|
|
1. determinar o produto do vector (a,b) pelo número real c; |
2. determinar o produto do vector (a, b) pelo número real d e fazer uma rotação de 90º ao vector obtido |
|
|
|
|
3. adicionar os vectores obtidos em 1. e 2. |
|
O quociente entre z1 e z2 é o produto de z1 pelo inverso de z2, ou seja, z1/z2 = z1.z2-1
Na prática, basta multiplicar e dividir z1 por
z2
Chamamos potenciação a uma potência de expoente inteiro.
Tem-se: zn = z . z . ... . z (n vezes), n natural e, na forma trigonométrica zn = rn.cis(nq).
Chamamos radiciação a uma potência de expoente fraccionário.
Cada número complexo tem n raízes índice n, ou seja, a radiciação de números complexos dá-nos um conjunto de raízes.
Observemos que as raízes índice n de um número complexo z são as soluções da equação
wn = z
que, no corpo dos complexos, tem n raízes.
Sendo z = rcis q, as raízes índice n de z são dadas pela fórmula de de Moivre para a radiciação:
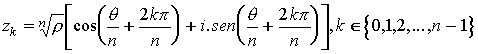
Euler demonstrou a seguinte igualdade:
que relaciona os números complexos e as funções
trigonométricas.
|
|
|
|
|
|
|
|
|
|
|
C é Corpo. Esta propriedade foi vista na página "O número imaginário existe realmente?" onde os números complexos foram vistos como pares de reais da forma (a, b). |
|
