A Sucessão de Fibonacci

   Foi no Liber Abaci que, pela 1ª vez, Fibonacci formulou o problema que haveria de ficar para sempre ligado ao seu nome. 

• Suponhamos que 1 casal de coelhos com um mês de idade (macho de fêmea) são ainda muito jovens para se reproduzir mas que, com dois meses de idades, já têm maturidade suficiente para o fazer. Admitamos também que todos os meses, a partir dos 2 meses de idade, dão origem a um novo casal (macho e fêmea).
• se todos os casais de coelhos se reproduzirem da mesma forma, quantos casais de coelhos haverá no fim de um ano?

   Para melhor compreender a génese do problema, suponhamos que o 1º casal de coelhos nasceu em Janeiro

Mês	Janeiro	Fevereiro	Março	Abril	Maio	Junho	Julho	Agosto
	0	0	1	1	2	3	5	8
	1	1	2	3	5	8	13	21

   Ao fim de um ano prevê-se que existam 144 casais de coelhos

   Se definirmos

             =nº de casais de coelhos no n-ésimo mês

    então temos que

             = 1 = 1º número de Fibonacci

            = 1 = 2º número de Fibonacci

             = 2 = 3º número de Fibonacci

             = 3 = 4º número de Fibonacci

             = 5 = 5º número de Fibonacci

            = 8 = 6º número de Fibonacci

   Se reparar-mos bem, a partir da 2ª ordem, cada termos é obtido através da soma dos dois termos imediatamente anteriores, ou seja,

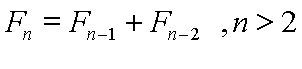
   Além disso, = 1 =

   É esta sequência de números reais que constitui a Sucessão de Fibonacci 

^***

Só no séc. XIX é que Edouard Lucas, pela primeira vez,  liga o nome de Fibonacci a esta sucessão.

 Mas, ao longo dos séculos, muitos foram os matemáticos queficaram perplexos, e até mesmo fascinados, com as propriedades e com a diversidade das áreas em que pode ser aplicada a Sucessão de Fibonacci.