Natureza

A ocorrência da sucessão de Fibonacci na Natureza é tão frequente que é difícil acreditar que seja acidental.

Vejamos alguns exemplos:

• Pétalas

Se, da grande diversidade de flores que existem, seleccionarmos o jarro, a rosa selvagem, a tormentilha, o cosmo, o rainúnclo amarelo, a columbiana, a asterácea, a flor-de-lis e a íris, podemos constatar que o número de pétalas destas flores é um número de Fibonacci.

• Estames

Mas, se optarmos por outra lista de flores tais como o áster, o cosmo e o malmequer, concluímos que é agora o número de estames que é um número de Fibonacci.

• Arranjo das folhas, dos ramos e dos caules

Se seleccionamos uma folha qualquer numa haste e lhe atribuirmos o número zero, se, depois, contarmos o número de folhas (admitindo que nenhuma se partiu) até à folha que está com a mesma orientação que a folha zero, verificaremos que o número total de folhas é um número de Fibonacci. 

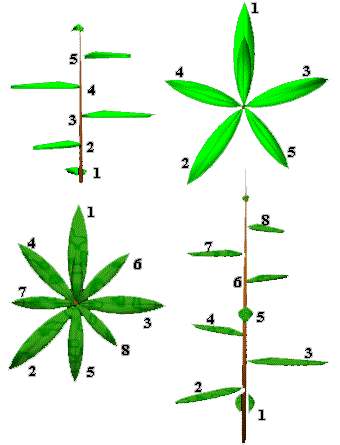
Além disso, o número de voltas da espiral que se percorre até chegar à última folha também é um número de Fibonacci.

• Pinhas

Os números de Fibonacci estão de tal modo presentes nas pinhas que, por vezes, são mesmo designados como "números das pinhas".

Na verdade, se considerarmos os termos consecutivos, para a esquerda e para a direita, das espirais formadas pelas escamas das pinhas concluímos que se trata de números de Fibonacci.

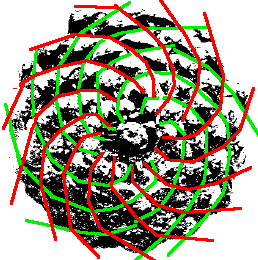
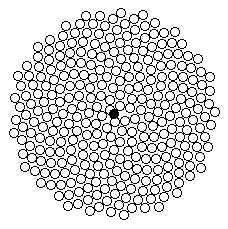
Aliás, acontece exactamente o mesmo com o girassol

  Na natureza, podemos até encontrar alguns números que são números de Lucas consecutivos. É o caso do ananás. Contando o número de espirais formadas pelas escamas hexagonais da casca, veremos que também no ananás se observam os números de Fibonacci.