| Evariste
Galois nasceu na pequena aldeia francesa de Bourg-la-Reine,
no dia 25 de Outubro de 1811. Quando tinha apenas quatro
anos de idade, o seu pai foi eleito perfeito da sua localidade. Nicolas-Gabriel Galois era um homem culto e cortês e durante seu mandato conquistou o respeito da comunidade. Fora da política,
o seu
maior interesse parece ter sido a composição de versos satíricos.
Galois herdou do pai a veia poética e recebeu da mãe - Adelaide Marie
Dernante - a melhor instrução
possível até os 12 anos, idade em que passou a frequentar o Colégio
Real Louis-le-Grand,
em Paris. Aquela casa de ensino mais parecia uma relíquia da idade média,
dominada por um carrasco que fazia as vezes de director e com o qual o
jovem Galois entrou rapidamente em conflito. Normalizada a
vida no Liceu, Galois continuou a frequentar as aulas e a dar conta
das suas obrigações, graças principalmente à magnífica base
primária que sua mãe lhe havia dado. Apesar de ter brilhado como aluno, Galois jamais foi um estudante
atento. O seu espírito estava quase sempre ausente. Aquelas
prelecções nada representavam para ele pois
nele já despontava o "gérmen" da criação.
Quando Galois tinha 16 anos, a Matemática invadiu a sua vida. Os livros
de matemática que circulavam no Liceu nunca
lhe mereceram atenção. Eram demasiados triviais.
O
gosto
de Galois pela matemática, logo superou a
capacidade do seu professor, e assim ele passou a estudar directamente dos
livros dos génios da época.
|
|
Isto ocorreu
em Fevereiro de 1827, quando descobriu textos de Legendre sobre geometria,
que lê rápida e sofregamente
e que interpreta tão bem quanto o seu autor.
Logo após, lê uma outra obra original de Lagrange
: Resolução de Equações
Numéricas (Equações Algébricas) Teoria das Funções Analíticas
e Lições sobre o Cálculo de Funções. Agora sim, havia um caminho
claro para o jovem prodígio. |
|
Todavia, o seu brilho seria (e foi, como se
veio a verificar!) o maior obstáculo ao seu sucesso. Embora soubesse
mais matemática do que seria necessário para passar nas provas do Liceu,
as soluções de Galois eram tão sofisticadas e inovadoras
que seus professores não conseguiam julgá-las correctamente.
Galois
andava entusiasmado, chegando mesmo a ser não só elogiado por um
professor, como também pelo director que terá constatado o seguinte:
|
"
É a paixão pela matemática que o domina. Eu penso que seria melhor
para ele se os seus pais lhe permitissem estudar apenas isto. Ele
está a desperdiçar o seu tempo aqui e nada mais faz do que
atormentar os seus professores e sobrecarregar-se de punições.
"
|
|
Na
realidade, com o seu temperamento explosivo, o jovem génio ia
paulatinamente conquistando a inimizade dos seus tutores e
de todos os que se cruzavam no seu caminho.
|

|
Galois tentou o exame na École
Polytechnique, sem a ajuda usual de um
curso preparatório em matemática. Foi reprovado, mas não desistiu. No mesmo ano, 1828,
frequentou o curso de Louis Paul Emile
Richard, um distinto professor de matemática, professor esse, que
lhe reconheceu o génio precoce e lhe facilitou o acesso à
leitura de trabalhos contemporâneos de Abel,
Cauchy,
Gauss
e Jacobi
. Emile Richard encorajou Galois, e
defendeu a ideia de que ele deveria ser admitido sem necessidade de
um exame. |

|
|
Gauss |
Jacobi |
Os resultados deste encorajamento foram espectaculares. Galois
publicou o seu primeiro trabalho ("Prova de um Teorema sobre
Fracções Periódicas Contínuas") em Abril de 1829 nos "Annales
de Gergonne". Um ano após a primeira tentativa, apresenta-se novamente a exame de admissão para a École Polytechnique
embora, mais uma vez,
os seus "saltos" lógicos na prova oral só tenham servido para
confundir o seu
examinador, Monsieur Dinet. Sentindo que estava prestes a ser
reprovado pela segunda vez, e frustrado por não sentir reconhecimento
pela sua inteligência, Galois perdeu a calma e atirou um apagador a Dinet,
acertando-lhe em cheio. A entrada na ilustre École
Polytechnique, ficou assim irremediávelmente comprometido.
Sem se deixar abalar pelas reprovações, Galois continuou confiante no
seu talento matemático. O seu
principal interesse era a teoria das equações (agora, chamada
«Teoria de Galois»). Nessa época, o jovem matemático estava ocupado
com equações algébricas e tinha reparado que não conseguia
resolver as de quinto grau. Hoje boa parte dos estudantes sabem resolver
equações do primeiro e do segundo graus. Resolvê-las significa achar o
"x" que torna a igualdade verdadeira, e no primeiro caso a solução
é quase instantânea. Já para as de 2º grau, não é tão trivial e existe
uma técnica de resolução chamada "Fórmula de Báskara" (em
homenagem a um sábio hindu do século XII) que permite solucioná-la
apenas com os números que aparecem na equação ao lado dos "x",
chamados na gíria matemática, de coeficientes ou
"radicais". As equações do terceiro e quarto grau também tem
soluções, ou fórmulas, do tipo Báskara, só que mais
complicadas.
A pergunta
que Galois colocou foi se haveria ou não, algo parecido para equações
do quinto grau. Foi apartir daqui que Galois desenvolveu a sua teoria. Postulou que "uma equação algébrica
pode ser resolvida por meio de radicais se, e só se, o seu grupo for resolúvel"(explicado na página "Obra de Galois"),
formulação na qual pela
primeira vez, aparece a palavra "grupo". A partir do estudo
efectuados por Galois ficou provado que não existe uma fórmula do tipo Báskara (vulgarmente
conhecida como fórmula resolvente) para equações
de grau maior ou igual a 5, ou seja, que permita obter a solução, ou o
"x" a partir dos coeficientes. Entre
o estudo que o jovem matemático fez, possa não espantar quem
não está dentro da matemática, a verdade é que as aplicações que posteriormente
surgiram demonstram a
grande importância do seu resultado.
No
dia 1 de Junho de 1829, ainda com 17 anos, Galois apresentou à Academia
de Ciências de Paris, as suas primeiras pesquisas sobre a solubilidade de
equações de grau primo. Augustin Louis Cauchy foi designado juiz.
|
Este ponto é bastante polémico e tem sido pomo de discórdia entre todos aqueles que têm escrito sobre
Galois. Alguns afirmam que Cauchy, perdeu ou se
esqueceu dos papéis e, por isso, nunca deu uma resposta,
"ocasionando um dos maiores desastres na história da matemática".
Outros afirmam que, intencionalmente, Cauchy os
teria deitado fora. Recentemente,
surgiram novos factos sugerindo que Cauchy tinha
planeado apresentar o trabalho de Galois na Academia de
Ciências de Paris em Janeiro de 1830. |
.jpg)
|
|
Cauchy |
A 29 de Dezembro
de 1829, Galois é admitido na École Normale Supérieure.
O seu examinador de matemática anotou o seguinte:
Já o examinador de literatura, contrastando com as palavras do colega
de matemática, disse:
|
Infelizmente,
nos três anos seguintes, uma série de tragédias pessoais destruiram as ambições de
Galois, nomeadamente, ficou sem o seu
pai, que se suicidou após uma campanha de difamação perpectuada por um sacerdote jesuíta. |
|

|
Galois
tenta novamente o
reconhecimento do seu talento, enviando para o secretário da Academia
de
Ciências de Paris, Joseph Fourier, uma nova versão de seus
trabalhos. Cabia a Fourier
entregar todo o trabalho de
Galois ao comité avaliador. Uma nova tragédia se abateu sobre
Galois
quando Fourier morre
algumas semanas antes da data da decisão dos juízes e, embora um maço
de trabalhos tenha sido entregue ao comité, o de Galois não
estava entre eles. Galois considerou que o seu trabalho foi
propositadamente perdido, por razões políticas, pela Academia
das
Ciências de Paris. |
|
Joseph Fourier |
|
Uma crença que foi reforçada no ano seguinte, quando a
Academia rejeitou o seu novo manuscrito, alegando que os "seus
argumentos não eram suficientemente claros nem suficientemente
desenvolvidos". |
| No
ambiente escaldante de forte agitação política que então se vive
em Paris, Galois frequenta meios republicanos e é expulso da Escola
Normal. Pouco tempo
depois, Galois
entregou a Poisson
um artigo que
continha a sua teoria, mas este
classificou-o de "incompreensível".
|
 |
|
Poisson |
|

|
No relatório elaborado por Poisson, poderia ler-se ainda, em jeito de
conclusão: "Fizémos
todos os esforços para compreender as demonstrações do Sr.
Galois. A sua argumentação não é suficientemente clara nem está
suficientemente desenvolvida para nos permitir ajuizar da sua correcção;
não chega a ser possível ter uma ideia desse artigo. O autor afirma que
as proposições contidas no seu manuscrito são parte de uma teoria geral
que tem grandes aplicações. Muitas vezes, as diferentes partes de uma
teoria clarificam-se mutuamente e podem ser mais facilmente
compreendidas quando tomadas em conjunto do que isoladamente. Para
formar uma opinião definitiva, deve portanto aguardar-se que o autor
publique o seu trabalho numa versão mais completa." cit
in Estrada, 2000, pág.541/542
|
| |
|
|
No dia 4 de Dezembro de 1830 Galois, alistou-se na Artilharia da Guarda Nacional. Tratava-se de
um ramo da milícia conhecido também como "Amigos do Povo".
Porém, antes do fim do mês, o rei extinguiu a Artilharia da Guarda Nacional.
Galois viu-se desamparado e sem casa. Nessa altura, Sophie Germain,
preocupada com o futuro de Galois, escreveu ao seu amigo Libri, também
matemático, o seguinte: |
|
|
"
(...) a morte de Monsieur Fourier constituiu um golpe
sobre o estudante Galois que, apesar de sua impertinência, mostrou
sinais de grande talento. Tudo isso fez com que ele fosse expulso
da École Normale. Está sem dinheiro. Há quem diga que Galois está completamente louco.
Temo que seja verdade."
|
|
Enquanto a paixão de Galois pela política continuava, era inevitável
que sua sorte fosse cada vez menor. Galois foi detido durante um mês na
prisão de Sainte-Pélagie, após um episódio ilustre testemunhado por
Alexandre Dumas no qual Galois, num banquete republicano, foi apanhado a
fazer um brinde ao rei Luís Filipe com um punhal na mão. No Dia da Bastilha, Galois
marchou em Paris com o uniforme da proscrita Artilharia da Guarda Nacional. Foi
condenado a seis meses de prisão e voltou para Sainte-Pélagie. Em meados de Março de 1832, um mês antes
da sentença, surge em Paris uma epidemia de cólera, que teve como efeito
a libertação de prisioneiros. O que aconteceu com Galois
nas semanas seguintes tem sido motivo de muita especulação mas o
que se sabe com certeza é que a tragédia foi o resultado de um romance
com uma mulher misteriosa, chamada Stéphanie-Félicie Poterine du Motel.
|
Stéphanie estava comprometida com um cidadão chamado Pescheux
d'Herbinville que descobriu a infidelidade da noiva e desafiou Galois
para um duelo à pistola. Galois conhecia muito bem a perícia de seu
desafiante. Na noite anterior ao confronto, noite que
acreditava ser a última da sua vida, Galois
escreveu
diversas cartas a amigos explicando-lhes
as circunstâncias e a razão das suas atitudes e decisões e procurou registar as suas
descobertas matemáticas. |

|
Num esforço desesperado, trabalhou
toda a noite, demonstrando o teorema que acreditava ser necessário para
explicar o enigma da equação de quinto grau. As páginas eram, na maior
parte, uma transcrição das ideias que já tinha enviado a Cauchy e
Fourier. No final da noite, quando os cálculos
ficaram completos,
escreveu uma carta ao amigo Auguste Chevalier, pedindo-lhe que, caso
morresse, enviasse aquelas páginas a todos os grandes matemáticos
da Europa.
Eis alguns excertos de uma célebre carta de Galois a Auguste
Chevalier:
|
Mon cher Ami,
J'ai fait en analyse plusieurs choses
nouvelles. Les unes concernent la théorie des équations algébriques;
les autres, les fonctions intégrales.
Dans la théorie des équations, j'ai recherché
dans quels cas les équations étaient résolubles par des radicaux
; ce qui m'a donné occasion d'approfondir cette théorie, et de décrire
toutes les transformations possibles sur une équation, lors meme
qu'elle n'est pas résoluble par radicaux.
On pourra faire avec tout cela trois Mémoires.
Le premier est écrit; et, malgré ce qu'en a
dit Poisson, je le maintiens avec les corrections que j'y ai faites.
Le second contient des applications assez
curieuses de la théorie des équations. Voici le résumé des
choses les plus importantes.
1* D'après les propositions II et III du
premier Mémoire, on voit une grande différence entre adjoindre à
une équation une des racines d'une équation auxiliaire, ou les
adjoindre toutes.
Dans les deux cas, le groupe de l'équation se
partage par l'adjonction en groupes tels que l'on passe de l'un à
l'autre par une meme substitution; mais la condition que ces groupes
aient les memes substitutions n'a lieu certainement que dans le
second cas. Cela s'appelle la décomposition propre.
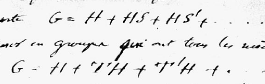
|
En d'autres termes, quand un groupe G en
contient un autre H, le groupe G peut se partager en groupes, que
l'on obtient chacun en opérant sur les permutations de H une meme
substitution ; en sorte que G = H + H S + H S' + ... Et
aussi, il peut se décomposer en groupes qui ont toutes les memes
substituions G = H + T H + T' H + ... Ces deux genres de décompositions
ne coincident pas ordinairement. Quand elles coincident, la décomposition
est dite propre.
|
Il est aisé de voirque que quand le groupe d'une
équation n'est susceptible d'aucune décomposition propre, on aura
beau transformer cette équation, les groupes des équations
transformées auront toujours le meme nombre de permutations.
Au contraire, quand le groupe d'une équation
est susceptible d'une décomposition propre, en sorte qu'il se
partage en M groupes de N permutations, on pourra résoudre l'équation
donnée au moyen de deux équations : l'une aura un groupe de M
permutations, l'autre un de N permutations.
Lors donc qu'on aura épuisé sur le groupe
d'une équation tout ce qu'il y a de décompositions propres
possibles sur ce groupe, on arrivera à des groupes qu'on pourra
transformer, mais dont les permutations seront toujours en meme
ordre.
Si ces groupes ont chacun un nombre premier de
permutations, l'équation sera soluble par radicaux; sinon non.
Le
plus petit nombre de permutations que puisse avoir un groupe indécomposable,
quand ce nombre n'est pas premier est 5.4.3.
2* Les décompositions les plus simples sont celles qui ont
lieu par la méthode de M. Gauss.
Comme ces décompositions sont évidentes, meme dans la forme
actuelle du groupe de l'équation, il est inutile de s'arreter
longtemps sur cet objet.
Quelles décompositions sont praticables sur une équation qui ne
se simplifie pas par la méthode de M. Gauss ?
J'ai appelé primitives les équations qui ne peuvent pas se
simplifier par la méthodes de M. Gauss ; non que ces équations
soient réellement indécomposables, puisqu'elles peuvent meme se résoudre
par radicaux. Comme le lemme à la théorie des équations
primitives solubles par radicaux, j'ai mis en juin 1830, dans le
Bulletin Férussac, une analyse sur les imaginaires de la théorie
des nombres.
On trouvera ci-jointe la démonstration des théorèmes suivants.
1. Pour qu'une équation primitive soit
soluble par radicaux, elle doit etre de degré p^v, p étant
premier.
2. Toutes les permutations d'une pareille équation
sont de la forme
x_k.l.m... / x_ak +bl + cm + ... + f.
x_a1k +b1l + c1m + ... + g. ...
k,l,m ... étant v indices, qui , prenant
chacun p valeurs, indiquent toutes les racines. Les indices sont
pris suivant module p ; c'est-à-dire que la racine sera la meme
quand on ajoutera à l'un des indices un multiple de p.
Le groupes qu'on obtient en opérant toutes les substitutions de
cette forme linéaire contient en tout p^n (p^n-p) ...(p^n-p^n-1)
permutations.
|
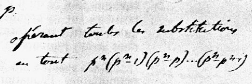
|
Il s'en faut que dans cette généralité les équations
qui lui répondent sont résoluble par radicaux. La condition
que j'ai indiquée dans le Bulletin de Férussac pour que l'équation
soit résoluble par radicaux est trop restreinte ; il y a peu
d'exceptions, mais il y en a. La dernière application de la théorie
des équations est relative aux équations modulaires des fonctions
elliptiques.
[ ... ]
Tu feras imprimer cette lettre dans la Revue Encyclopédique. Je me suis souvent hasardé dans ma vie à avancer
des propositions dont je n' étais pas sûr. Mais tout ce que j'ai
écrit là est depuis bientôt un an dans ma tête, et il est trop
de mon intérêt de ne pas me tromper pour qu'on me soupconne
d'avoir énoncé des théorèmes dont je n'aurais pas la démonstration
complète. Tu prieras publiquement Jacobi et Gauss de donner leur
avis, non sur la vérité, mais sur l'importance des théorèmes.
Après cela, il y aura, j'espère, des gens qui trouveront leur
profit à déchiffrer tout ce gachis. Je t'embrasse avec effusion.
Le 29 mai 1832,
E. Galois.
|
|
Ainda nessa noite, Galois, endereçou
um manifesto político a todos os republicanos, aos seus amigos e
companheiros, que rezava assim:
|
|
" (...) não me censurem se eu morrer por outro motivo que não pelo meu
país. Será que vou morrer por uma coisa tão insignificante e
vergonhosa ? Peço a Deus que testemunhe, pois fui coagido e cedi à
provocação. Mas, fiz tudo para a evitar. "
|
|
Na manhã seguinte, quarta-feira, 30 de Maio de 1832, num campo isolado,
perto de um pequeno lago, Galois e d'Herbinville enfrentaram-se a uma distância
de vinte e cinco passos, armados com pistolas. D'Herbinville estava
acompanhado de dois assistentes e Galois
estava sozinho.
Não contou a ninguém o seu drama e, mesmo a mensagem que enviou ao seu irmão, Alfred, só lhe
chegaria depois do duelo terminado. Também as cartas que escreveu na
noite anterior só chegariam aos seus amigos vários dias depois.
As pistolas foram erguidas e disparadas. D'Herbinville continuou de pé e
Galois foi atingido no estômago e, ficou deitado no chão. Não havia
nenhum cirurgião por perto e o vencedor foi embora calmamente deixando o
seu oponente ferido. Algumas horas depois, Galois foi levado
para o Hospital Cochin por um camponês que passava no local. No dia seguinte, nos braços do seu irmão, Alfred, e
após recusar os serviços de um padre, Evariste Galois faleceu. Tivesse
Galois vivido outros cinco meses, e teria completado 21 anos.
De referir por fim, que surge hoje a hipótese que dá como provável que
a sua morte se tenha ficado a dever a um tumor que tinha na cabeça e que
teria sido detectado durante
a autópsia a que foi sujeito.
Sobre o sentido quase heroico
vida vida de
Galois convidamo-lo ainda a ler um breve e inspirado
texto de Bento de Jesus Caraça.
|

.jpg)