![]()
e, reconhecendo os cubos e os quadrados, podemos dar ao facto observado a forma mais interessante:
![]() .
.
Como é que isto acontece? Será que, com frequência, uma tal soma de cubos sucessivos é um quadrado?
Ao colocar esta pergunta procedemos como o naturalista que, impressionado por uma planta curiosa ou por uma formação geológica surpreendente, concebe uma questão geral. A nossa questão geral está relacionada com a soma de cubos sucessivos
![]() .
.
Fomos levados a ela pelo “exemplo particular” n=4.
Polya apresenta um primeiro exemplo.
Através do caso particular
![]() Polya coloca a seguinte hipótese: será que a soma dos primeiros n
cubos é um quadrado?
Polya coloca a seguinte hipótese: será que a soma dos primeiros n
cubos é um quadrado?
O
autor tenta seguir os mesmos passos que o naturalista seguiria para provar a
existência de uma lei geral.
Como o naturalista, investiga os casos especiais n = 1, 2, 3 e 5, sendo que já conhecia o caso n=4.
|
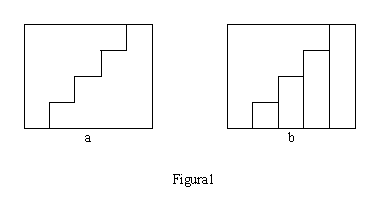
Que podemos fazer da nossa questão? O que o naturalista faria; podemos investigar outros casos especiais. Os casos especiais n=2,3 são ainda mais simples, o caso n=5 é o próximo. Acrescentemos, para salvaguardar a uniformidade e completude, o caso n=1. Arranjando elegantemente todos estes casos, como um geólogo arranjaria os espécimens de um certo minério, obtemos a seguinte tabela:
|
Arranjados “elegantemente”, ou seja, dispostos de um determinado modo, Polya constata que todos estes casos verificam a sua hipótese inicial.
É difícil acreditar que todas estas
somas de cubos consecutivos sejam quadrados por mero acaso. Do mesmo
modo, o naturalista teria poucas dúvidas de que a lei geral sugerida
pelos casos especiais até então observados não fosse correcta; a lei
geral é quase provada por indução. O matemático expressa-se com
maior reserva embora fundamentalmente pense da mesma forma. Ele diria
que o teorema seguinte é fortemente sugerido por indução:
A soma dos primeiros n cubos é um quadrado.
Surge
aqui surge
a diferença entre os dois processos em causa. Para o naturalista a lei
geral é quase provada por indução. Ora, Polya defende
que a matemática tem uma fase experimental muito parecida com as ciências
da natureza. No entanto, para um matemático a observação de alguns casos
particulares arranjados elegantemente apenas lhe permite dizer que o teorema é
fortemente sugerido, mas não permite provar a sua verdade.