A
Demonstração do quinto Postulado de Euclides por Proclus
Proclus
Diadochus nasceu em Constantinopla por volta do ano 410. Terá ido aprender
filosofia para Alexandria
e, como esse ensino não o satisfez, foi para Atenas,
estudar com Plutarco na Academia de
Platão. Mais tarde, terá chegado a
director da Academia, cargo que manteve até morrer, no ano 485. O seu “Comentário ao primeiro livro dos Elementos de
Euclides” é a principal fonte de
conhecimentos sobre a história antiga da geometria grega.
Proclus é aí bastante claro ao referir que o quinto postulado de
Euclides é um teorema e que pode ser demonstrado a partir dos restantes quatro
postulados.
Após transcrever o quinto postulado, Proclus
escreve:
|
“Este
[o quinto postulado] deve ser retirado do conjunto dos postulados. Pois é um
teorema – teorema este que coloca muitas questões que Ptolomeu se propôs resolver
num dos seus livros - e requer,
para a sua demonstração, várias definições assim como teoremas. E a sua recíproca
é provada pelo próprio Euclides como um teorema. Mas talvez algumas pessoas
pensem erradamente que esta proposição merece ser classificada entre os
postulados com base em os ângulos serem menores que dois ângulos rectos
fazer-nos de imediato acreditar na convergência e intersecção das linhas
rectas. A tais pessoas, Geminus deu resposta apropriada quando disse que aprendemos dos
próprios fundadores desta ciência a não prestar atenção a imaginações
plausíveis na determinação das proposições a serem aceites na geometria.
Aristóteles, do mesmo modo, diz que aceitar raciocínios prováveis de um geómetra
é como exigir provas de um retórico. E Simmias é levado por Platão a dizer
“Estou ciente que aqueles que fazem demonstrações a partir de
probabilidades são impostores.” Logo aqui, apesar de a afirmação que linhas
rectas convergem quando os ângulos rectos estão diminuídos ser verdadeira e
necessária, no entanto a conclusão de que, por elas convergirem mais quando são
prolongadas para mais longe, elas se irão encontrar a certa altura, é plausível,
mas não necessária, na ausência de um argumento
provando que isto é verdade para linhas rectas. Que há linhas que se
aproximam indefinidamente mas nunca se encontram parece ser implausível e
paradoxal. No entanto, é apesar disso verdade e foi verificado para outras espécies
de linhas. Não poderá isto, então, ser possível para linhas rectas como
essas? Até termos demonstrado firmemente que elas se encontram, o que é
dito acerca de outras linhas despoja a nossa imaginação da sua plausibilidade.
E apesar de os argumentos contra a intersecção destas linhas poderem conter
muito que nos surpreenda, não deveríamos nós recusar-nos a admitir
na nossa tradição este apelo sem razão à probabilidade?
Estas considerações tornam claro que devemos
procurar uma demonstração do teorema com que nos deparamos e que lhe falta o
carácter especial de um postulado”
(Proclus, séc V, 191.21-193.3)
|
Nesta passagem é visível a profunda crença
de que o quinto postulado de Euclides é demonstrável. Para Proclus, ele pode
ser provado racionalmente, não existindo por isso razão para o considerar como
postulado, pois a verificação do quinto postulado não se deve a um facto de
probabilidade (no sentido em que intuitivamente se vê que as rectas se
aproximarão cada vez mais e portanto provavelmente se encontrarão).
Proclus regressa à problemática do quinto
postulado quando chega à proposição 29 que refere ser a primeira em cuja
demonstração Euclides utiliza o quinto postulado. Escreve então:
|
“Como
eu disse na parte da minha exposição que precede os teoremas, nem todos
admitem que esta proposição geralmente aceite seja indemonstrável. Como
poderia isso ser quando a sua recíproca é registada entre os teoremas como
algo demonstrável? Pois o teorema que, em todo o triângulo, quaisquer dois ângulos
internos são menores que dois ângulos rectos é a recíproca deste postulado.
Visto também o facto que duas linhas rectas, quando prolongadas, aproximam-se uma
da outra cada vez mais não é, como eu disse anteriormente, um sinal de que
elas se encontrarão, porque foram descobertas outras linhas que convergem na
direcção uma da outra mais e mais mas nunca se encontram.
Por este motivo outros antes de nós
classificaram-no entre os teoremas e exigiram uma demonstração disto que foi
tomado como um postulado pelo autor dos Elementos.”
(Proclus,
séc V, 364.18-365.6)
|
Proclus reafirma a sua convicção de que o
postulado é de facto um teorema e portanto demonstrável. Por um lado, realça que, se a recíproca do postulado (proposição XVII) é um teorema
demonstrável, então também o deveria ser o postulado (o que não é verdade
pois, de facto, o postulado não é demonstrável e a sua recíproca é). Por
outro lado, realça a dificuldade dessa demonstração pelo facto de que duas linhas
estarem cada vez mais próximas, não implica necessariamente que se encontrem.
De destacar que Proclus aponta a
existência de “outros antes de nós” que também consideraram que este
postulado seria um teorema. Embora não conheçamos os seus nomes, ficamos a
saber da existência de uma comunidade exigente e interessada que, desde que Euclides escreveu
os Elementos, não deixou de estudar minuciosamente e de pôr em causa o seu
postulado número cinco.
É após este apontamento que Proclus fala de Ptolomeu
e do seu trabalho sobre o quinto postulado, transcrevendo a demonstração de Ptolomeu
do
postulado 29 e do quinto postulado de Euclides. Proclus aponta falhas nas
demonstrações de Ptolomeu
que classifica de fracas e insatisfatórias.
Analisa depois um argumento que defende que duas rectas, mesmo fazendo ângulos
inferiores a dois rectos com uma terceira recta que as intersecte, ainda assim, não se
intersectam as duas, não especificando quem ao certo é que defendia este
argumento que contraria o quinto postulado:
|
“Agora
examinemos aqueles que dizem que é impossível que linhas prolongadas de ângulos
menores que dois ângulos rectos se encontrem. Tomando duas linhas rectas AB e
CD e a linha AC caída sobre elas e fazendo os ângulos internos menores que
dois ângulos rectos, eles pensam que podem demonstrar que AB e CD não se
encontram. Seja AC bissectado em E, e seja um comprimento AF igual a AE,
colocado sobre AB, e sobre CD um comprimento CG igual a EC. É claro que AF e CG
não se encontrarão em nenhum ponto em FG; pois se elas se
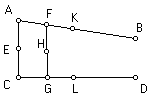
encontram,
dois lados de um triângulo serão iguais a um terceiro, AC, o que é impossível.
Outra vez desenhe-se a linha FG e bissectada em H, e sejam iguais comprimentos
colocados sobre [FK e GL]. Estes do mesmo modo não se encontrarão, pelas
mesmas razões que antes. Ao fazer isto indefinidamente, desenhando linhas entre os pontos não-coincidentes, bissectando as linhas de ligação, e colocando
sobre as linhas rectas comprimentos iguais às suas metades, eles dizem que
provam que as linhas AB e CD não se encontrarão em local algum.
Estes são os seus argumentos. A eles
temos que responder que o que dizem é verdade mas que não prova tanto quanto
pensam. É verdade que não é possível deste modo simples encontrar o ponto em
que a intersecção ocorre. Não é verdade, no entanto, que as linhas nunca se
encontram. Seja considerado que AB e CD não se encontram quando os ângulos BAC
e DCA são definidas pelos pontos F e G. Mas não há razão pela qual elas não
devam encontrar-se em K e L, mesmo que FK e GL sejam iguais a FH e HG. Pois se
AK e CL se encontram em K e L, os ângulos KFH e LGH não serão mais os mesmos;
isto é, parte de FG passou a pertencer a AK e CL; e assim em troca as linhas FK
e GL são maiores que a base por tanto quanto tiraram da linha FG. Isto também
deveria ser dito. Ao afirmar sem restrição que linhas prolongadas de ângulos
menores que dois ângulos rectos não se encontram, eles estão derrubando o que
não pretendem. Seja o diagrama igual ao anterior.
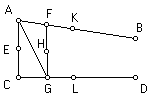
Agora é
possível
ou não desenhar uma linha recta de
A a G? Se eles dizem que não é possível, estão a negar, não apenas o
quinto postulado, mas também o primeiro, que afirma ser possível desenhar uma
linha recta de qualquer ponto a outro qualquer ponto. Se isto é possível, seja
desenhada essa linha. Então como os ângulos FAC e GCA são menores que dois ângulos
rectos, é ainda mais claro que GAC e GCA são menores que dois ângulos rectos.
Portanto AG e CG encontram-se em G, e são prolongadas de ângulos menores que
dois ângulos rectos. Consequentemente não é possível dizer sem restrição
que linhas prolongadas de ângulos menores que dois ângulos rectos não se
encontram. Pelo contrário, é claro que algumas linhas prolongadas de ângulos
menores que dois ângulos rectos encontram-se, se bem que o argumento que prova
isto de todas essas linhas ainda está por ser encontrado. Dado que “menor que
dois ângulos rectos” é indeterminado, poderia dizer-se que com uma tal e tal
redução [aos ângulos rectos] as linhas rectas continuam não secantes,
enquanto que, com outra redução maior [aos ângulos rectos] que esta, elas
encontram-se.”
(Proclus,
séc V, 369.1-371.10)
|
Aparentemente, este argumento mostraria que as rectas nunca se
intersectariam. Contudo, a verdade é que, de modo análogo ao que se passa com
o paradoxo de Aquiles e da Tartaruga, o processo não tem fim mas as rectas
encontram-se numa distância finita. Proclus não foi capaz de detectar a falha
no argumento apresentado e, na sua análise, parece perder-se (refiro-me à parte
que coloquei a itálico e cujo sentido não consegui perceber; talvez seja falha
minha, mas quer-me parecer que falta algo no raciocínio; talvez algo se tenha
perdido entre as várias traduções ao longo dos tempos). Contudo, compreende
que, apesar de este método nunca encontrar o ponto de intersecção, isso não
significa que as rectas nunca se intersectem.
Proclus aponta que a conclusão deste argumento não faz sentido pois
prova “demais”, no sentido em que contraria não só o quinto postulado mas
também o primeiro, segundo o qual se poderia traçar uma linha recta ligando A
a G. Segundo o argumento por Proclus analisado, a recta AG nunca intersectaria a
recta CD e, logo, não chegaria a G, o que é absurdo. Deste modo, Proclus afirma que não
há dúvida que existem rectas que se intersectam, embora, Proclus avise que
ainda não foi encontrado o “argumento” que prova isso para todas as rectas,
ou seja, que ainda não foi demonstrado o quinto postulado de Euclides.
É neste contexto que Proclus prossegue com o seu
“argumento” para demonstrar o quinto postulado de Euclides, começando por
afirmar a necessidade de aceitar à partida um certo axioma:
|
“A quem quiser ver este argumento
construído, digamos que terá que aceitar antecipadamente um axioma como o que
Aristóteles usou para estabelecer a finitude do universo: se de um ponto único
duas linhas rectas fazendo um ângulo são prolongadas indefinidamente, o
intervalo entre elas quando prolongadas indefinidamente excederá qualquer
grandeza finita. Pelo menos ele provou que, se as linhas estendidas do centro
para a circunferência são infinitas, o intervalo entre elas é infinito; pois
se é finito, é possível aumentar o intervalo entre elas, de modo que as
linhas rectas não sejam infinitas. As linhas rectas estendidas indefinidamente,
então, divergirão uma da outra uma distância maior que qualquer grandeza
finita.”
(Proclus,
séc V, 371.11-371.23)
|
Há quem critique este axioma pressuposto por Proclus dizendo que também
ele teria que ser demonstrado, pois o argumento que Aristóteles usa para concluir a
finitude do universo não prova este axioma. É o caso de Clavio, que criticou o
axioma e que diz que, do mesmo modo que não se pode supor que duas
linhas que se aproximam cada vez mais se irão intersectar, também não se pode
supor que duas linhas que se afastam cada vez mais se irão afastar mais do que
qualquer distância finita, dando o exemplo da conchóide de Nicomedes, que se
afasta cada vez mais da tangente no vértice mas nunca se afasta mais do que uma
determinada distância finita. Contudo, este axioma, se bem que possa ser
considerado discutível, não é equivalente e não permite provar o quinto
postulado.
É então que Proclus, partindo deste axioma, apresenta a sua própria demonstração do
quinto postulado:
|
“Se
isto é estabelecido, eu digo que, se uma linha recta corta uma de duas rectas
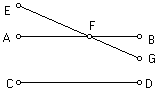
paralelas,
ela corta a outra também. Sejam AB e CD linhas paralelas e EFG uma linha que
corta AB. Eu digo que também corta CD. Pois, como existem duas linhas rectas
passando por um ponto F, quando FB e FG são estendidas indefinidamente, elas
terão entre elas um intervalo maior que qualquer grandeza e, por isso, maior que
a distância entre as linhas paralelas. E, portanto, quando são separadas uma da
outra uma maior distância que aquela entre as linhas paralelas, FG cortará CD.
Portanto, se uma linha recta corta uma de duas paralelas, ela cortará a outra
também.
Provado isto, podemos demonstrar a
proposição perante nós [o quinto postulado] como sua consequência. Sejam AB
e CD duas linhas rectas e EF caída sobre elas e a fazer ângulos BEF e DFE
menores que dois ângulos rectos.
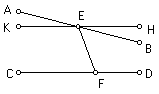
Eu
digo que as linhas rectas encontrar-se-ão no lado em que os ângulos são
menores que dois ângulos rectos. Pois, como os ângulos BEF e DFE são menores
que dois ângulos rectos, seja HEB igual ao excesso de dois ângulos rectos
sobre eles [seja HEB dois ângulos rectos menos BEF e DFE], e seja HE prolongada
até K. Então, como EF cai sobre KH, e CD faz os ângulos internos iguais a dois
ângulos rectos, nomeadamente HEF e DFE, HK e CD são linhas rectas paralelas. E
AB corta KH; irá portanto cortar CD, pela proposição já demonstrada. AB e CD
portanto encontrar-se-ão na direcção
em que os ângulos são menores que dois ângulos rectos, pelo que a proposição
perante nós foi demonstrada.”
(Proclus,
séc V, 371.23-373.3)
|
Como se verifica, Proclus começa por apresentar a demonstração de uma proposição que
diz que uma linha recta que encontra uma de duas paralelas também intersecta
necessariamente a outra. É daí que prova o quinto postulado e, de facto, a partir
dessa proposição pode-se demonstrar o quinto postulado de Euclides.
Proclus não cai pois no erro de considerar a definição
de paralelismo de Possidónio (rectas equidistantes) como equivalente à de Euclides
(rectas que não se intersectam), o que seria pressupor desde logo o quinto
postulado. Contudo, considera que a distância entre duas paralelas se mantém
menor que uma distância fixa, na demonstração da proposição inicial (a
partir da qual demonstrou o quinto postulado) e é aí que está o seu erro, pois isso
é equivalente ao quinto postulado de Euclides (na geometria hiperbólica, é
falso que a distância entre duas paralelas seja sempre inferior a uma certa
distância finita). Logo acaba por não demonstrar o postulado visto que o
pressupôs, ainda que involuntariamente.
Apesar disso, o trabalho de Proclus é
extremamente relevante. Ele
preocupou-se em apresentar a questão de uma forma ponderada e científica. Não
se limitou a apresentar a sua demonstração. Analisou uma tentativa anterior à
sua (a de Ptolomeu, que correctamente identificou como errada) e atacou, por um
lado, aqueles que diziam que as rectas nunca se encontravam e, por outro, aqueles
que se fundamentavam em “probabilidades” para concluir que as rectas tinham
que se encontrar só porque a tendência das rectas era aproximar-se cada vez
mais.
Na sua tradução do comentário de
Proclus, Morrow considera que “esta tentativa de provar o quinto postulado de
Euclides é a contribuição mais ambiciosa de Proclus para os elementos da
geometria” (Morrow, 1970, xxxi). Há mesmo quem ponha a hipótese, a partir de
uma referência de Philoponus, que Proclus teria tido este assunto em tão elevada
conta que teria mesmo chegado
ao ponto de escrever um livro sobre ele, entretanto perdido.
Topo



