A
Demonstração do quinto Postulado de Euclides por Ptolomeu
Ptolomeu, ou Claudius Ptolemaeus, foi geógrafo e astrónomo e viveu no século II,
em Alexandria. Foi o autor de um famoso tratado de astronomia em 13 livros, que chegou até à actualidade
através de uma tradução árabe: Almagesto.
Porém, é num outro livro que Ptolomeu apresenta a sua demonstração do quinto postulado de
Euclides. O livro (que não chegou até
aos nossos dias) intitulava-se “Que linhas prolongadas de ângulos menores que dois ângulos
rectos encontram-se uma com a outra”. O título pode hoje não fazer muito
sentido. Mas, se
se tiver em conta que aí se apresenta um estudo sobre o quinto postulado de
Euclides (e até uma demonstração), compreende-se que o que Ptolomeu
afirma no título do livro é precisamente o quinto postulado de Euclides, no
sentido em que os ângulos que refere são os dois ângulos também referidos no
dito postulado como menores que dois rectos.
A propósito da proposição 29 e referindo-se a Ptolomeu,
Proclus escreve: “a sua
demonstração [do quinto postulado] utiliza muitos dos teoremas estabelecidos pelo
autor dos Elementos precedentes a este [a proposição 29]” (Proclus, séc
V, 365.8-10). Embora não reproduza toda a argumentação que Ptolomeu utilizou para demonstrar esses teoremas,
Proclus apresenta as
demonstrações de Ptolomeu para as proposições 28 e 29 dos Elementos e para o quinto postulado de Euclides.
Proposição
28 - Se uma linha recta ao cortar outras duas, fizer o ângulo
externo igual ao ângulo interno oposto do mesmo lado, ou se a soma dos ângulos
internos do mesmo lado for igual a dois ângulos rectos, então, as linhas
rectas são paralelas entre si.
Vejamos a demonstração da proposição 28 do livro I
dos Elementos de Euclides feita por Ptolomeu a partir do modo como Proclus
a transcreve:
|
“Sejam
AB e CD duas linhas rectas cortadas por uma linha recta EFGH de modo a fazer os
ângulos BFG e FGD iguais a dois ângulos rectos. Eu digo que as linhas rectas
são paralelas, isto é, não secantes. Se possível, sejam FB e GD prolongadas
até se
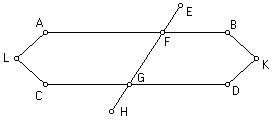
encontrarem
em K. Então, como a linha recta GF corta a linha AB, ela faz os ângulos AFG e
BFG iguais a dois ângulos rectos. Do mesmo modo, como GF corta CD, ela faz os
ângulos CGF e DGF iguais a dois ângulos rectos. Consequentemente os ângulos
AFG, BFG, CGF e DGF são iguais a quatro ângulos rectos, dos quais dois, BFG e
DGF, estão determinados como iguais a dois ângulos rectos; por este motivo os
outros dois ângulos, AFG e CGF, são também iguais a dois ângulos rectos.
Se então, quando os ângulos internos são iguais a dois ângulos rectos
as linhas FB e GD quando prolongadas encontram-se uma à outra em K, logo
também FA e GC quando prolongadas irão encontrar-se, pois os ângulos AFG e
CGF são também iguais a dois ângulos rectos. As linhas rectas irão
encontrar-se ou em ambos os lados ou em nenhum se estes [os ângulos internos
deste lado], como aqueles [ângulos internos do outro lado], forem iguais a dois
ângulos rectos. Suponhamos então que FA e GC encontram-se em L. Então as
linhas rectas LABK e LCDK cercam uma área, o que é impossível. É por isso
impossível que linhas se encontrem quando os ângulos internos são iguais a
dois ângulos rectos. Por isso elas são paralelas.”
(Proclus,
séc V, 362.20-363.18)
|
Na transcrição apresentada vê-se que Ptolomeu
utiliza uma definição de paralelismo que coincide com a de Euclides, ou seja,
as linhas rectas são paralelas se não se intersectarem (não secantes). Não
é esse o seu erro na demonstração do postulado.
É sabido que esta proposição é demonstrável,
no entanto, a dada altura, Ptolomeu parece cometer um erro ao não justificar
devidamente um passo da demonstração, em que conclui do particular para o
universal uma suposição. Nesta demonstração Ptolomeu queria provar que duas
linhas que satisfazem certas condições nunca se intersectam, mas não pode fazê-lo
ao provar que é um absurdo que as linhas que satisfazem essas condições se
encontram sempre, que é o que é feito quando diz que se FB e GD se
encontram, então AF e CH também se encontram (por ambas satisfazerem as tais
condições). O que Ptolomeu tinha que provar
era que se FB e GD se encontrarem isso implica um absurdo. Contudo, aparentemente, Ptolomeu não se
limita a tomar por hipótese que FB e GD se encontram pois, diz que se FB e GD se encontram, então
AF e CH também se encontrarão por estarem nas mesmas condições. Ora, então,
já está a supor que todas as linhas nas referidas condições (os ângulos
internos que fazem, num dos lados, com uma recta que as intersecte a ambas, são
iguais a dois ângulos rectos) se intersectam, não pondo a hipótese que,
algumas vezes, se encontram mas não necessariamente sempre. Só assim seria a negação
da proposição e que se reduzida ao absurdo provaria a proposição, como
pretendia.
O erro de lógica que Ptolomeu comete é que para provar que
A=“Todas as rectas com as quais uma terceira recta que as intersecte faz ângulos
internos num lado cuja soma é igual a 180º, não se intersectam”, não
basta provar que é absurdo B=“Todas as rectas com as quais uma terceira recta
que as intersecte faz ângulos internos num de um lado cuja soma é igual a 180º,
intersectam-se”. Este tipo de demonstração é válida se demonstrarmos que a negação
da proposição que pretendemos provar leva a um absurdo. Contudo, a negação
de A é C=“Há rectas com as quais uma terceira recta que as intersecte faz ângulos
internos num lado cuja soma é igual a 180º, e que se intersectam”.
Ptolomeu supõe que todas as rectas com as quais uma terceira recta que as
intersecte faz ângulos internos num lado cuja soma é igual a 180º se
intersectam e portanto apenas prova D=“Há rectas com as quais uma terceira
recta que as intersecte faz ângulos internos, de um lado, cuja soma é igual a
180º, e que não se intersectam”.
Nesta demonstração, o erro acaba por não ter
consequências pois, aquilo que Ptolomeu supõe sem apresentar justificação,
pode ser demonstrado. Para a demonstração estar completa, Ptolomeu teria de justificar o que diz e
mostrar que, se de um lado estas rectas se intersectam, o mesmo teria de
acontecer do outro lado. Citando Heath (1925, p. 204):
|
“seria
mais claro se tivesse sido mostrado que os dois ângulos internos num lado de EH
são respectivamente iguais aos dois ângulos no outro lado, nomeadamente
BFG a CGF e FGD a AFG; donde, ao assumir que FB e GD encontram-se em K, podemos
tomar o triângulo KFG e colocá-lo (por exemplo através da rotação em torno
do ponto médio de FG) de modo a que FG caia onde está GF na figura e GD caia
sobre FA, e assim FB tem de cair
sobre GC; por isso, como FB e GD encontram-se em K, GC e FA também têm de
encontrar-se num ponto correspondente L.”
|
Vejamos agora a demonstração apresentada por
Ptolomeu para a
proposição 29. Mais uma vez, Ptolomeu não usa o quinto postulado. Mas, como
era de esperar, a demonstração está
incorrecta, pois é impossível prová-la sem este postulado.
Proposição
29 - Uma linha recta que corta duas linhas
rectas paralelas faz os ângulos alternos iguais entre si, o ângulo externo
igual ao ângulo interno oposto e a soma dos ângulos internos do mesmo lado
igual a dois ângulos rectos.
Eis a transcrição de Proclus da demonstração de Ptolomeu:
|
“Eu
digo, por isso, que a reciproca é também verdadeira, isto é, que quando
linhas rectas paralelas são cortadas por uma linha recta, os ângulos internos
no mesmo lado são iguais a dois ângulos
rectos. Como é necessário que a linha que corta as linhas paralelas faça os
ângulos internos no mesmo lado ou iguais a dois ângulos rectos ou menores ou
maiores que dois ângulos rectos. Sejam AB e
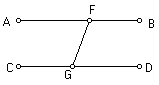
CD
linhas paralelas, e seja GF uma recta que cai sobre elas. Eu digo que não faz
os ângulos internos no mesmo lado maiores que dois ângulos rectos. Pois se os
ângulos AFG e CGF são maiores que dois ângulos rectos, os restantes ângulos
BFG e DGF, são menores que dois ângulos rectos. Mas estes mesmos ângulos são
também maiores que dois ângulos rectos; pois AF e CG não são mais paralelas
que FB e GD, logo, se a linha que cai sobre AF e CG faz os ângulos internos
maiores que dois ângulos rectos, então também a linha que cai sobre FB e GD
faz os ângulos internos maiores que dois ângulos rectos. Mas estes mesmos ângulos
são menores que dois ângulos rectos (pois os quatro ângulos AFG, CGF, BFG e
DGF são iguais a quatro ângulos rectos), o que é impossível. Analogamente nós
podemos provar que a linha que cai sobre as paralelas não faz os ângulos
internos na mesma direcção menores que dois ângulos rectos. Se, então, ela fá-los
nem maiores nem menores que dois ângulos rectos, a única conclusão restante
é que a linha que cai nelas faz os ângulos internos na mesma direcção iguais
a dois ângulos rectos. Tendo isto sido demonstrado, a proposição perante nós
[o quinto postulado] pode ser incontestavelmente provada.”
(Proclus,
séc V, 365.17-366.15)
|
Ao apresentar esta demonstração, Ptolomeu crê que,
provado isto, nada o impede de demonstrar o quinto postulado de Euclides. De
facto, Ptolomeu tem razão ao afirmar que, provada esta proposição, pode provar
o quinto postulado de Euclides. Contudo, esta demonstração é incorrecta.
Ptolomeu apresenta o argumento de que, se AB e CD são paralelas, como FB e GD são
tão paralelas de um lado quanto AF e CG são do outro, então a soma dos ângulos
internos de um lado teria de ser igual à soma dos ângulos internos do outro.
Mas, como Proclus referirá no seu comentário a esta demonstração, ele não
poderia assumir isso. O que este argumento tem que lhe permitirá demonstrar
esta proposição e depois o quinto postulado é o facto de que, afirmar que FA e
GC são tão paralelas para um lado quanto FB e GD são para o outro, é
equivalente a afirmar que, por qualquer ponto exterior a uma recta, passa uma única
paralela (Axioma de Playfair), que é equivalente ao quinto postulado de
Euclides. Logo, se não está a ser suposto o quinto postulado de Euclides, este
argumento não é válido e portanto a demonstração é incorrecta.
Assim sendo, se o quinto postulado não
é suposto, Ptolomeu comete nesta demonstração um erro lógico do mesmo tipo do que cometeu na demonstração da proposição anterior, pois para provar
que A=“Sempre que uma recta cai sobre duas rectas paralelas faz ângulos
internos do mesmo lado iguais a dois ângulos rectos” não basta provar que é
absurdo B=“Existe uma recta que sobre duas rectas paralelas ou faz ângulos
internos do mesmo lado maiores que dois rectos (nos dois lados da recta) ou faz
ângulos internos do mesmo lado menores que dois rectos (nos dois lados da
recta)” como faz Ptolomeu. A negação de A é C=“Existe uma recta que caída
sobre duas rectas paralelas, não faz ângulos internos do mesmo lado iguais a
dois ângulos rectos”, que deixa em aberto a hipótese de haver de um lado da
recta ângulos internos menores que dois ângulos rectos e do outro maiores que
dois ângulos rectos.
Para provar que os ângulos internos são rectos Ptolomeu
supõe, tendo em vista um absurdo, que a soma dos ângulos internos num lado é
menor ou maior que dois rectos. Mas também supõe (embora julgue deduzir)
que os ângulos internos do outro lado verificarão exactamente a mesma
propriedade, ou seja, pressupõe que, se de um lado são maiores, do outro também
o serão. Ora, o que tinha de provar era que, se de um lado os ângulos fossem
maiores ou menores que dois ângulos rectos, então sim estaríamos necessariamente
perante um absurdo (não
forçando a que do outro lado isso se verificasse, pois isso só é verdade se
considerar o quinto postulado ou seu equivalente).
Depois de julgar demonstrada a
proposição 29 sem utilizar o quinto postulado de Euclides, Ptolomeu prossegue
para a demonstração do próprio postulado (sem ter consciência que, para demonstrar a
proposição 29, já o havia utilizado implicitamente):
|
“Eu
digo que, se uma linha recta cai sobre duas linhas rectas e faz os ângulos
internos no mesmo lado menores que dois ângulos rectos, as linhas rectas se
prolongadas encontrar-se-ão nesse lado em que os ângulos são menores que dois
ângulos rectos. Suponhamos que elas não se encontram. Mas se elas são não
secantes no lado em que os ângulos são menores que dois ângulos rectos, muito
mais serão elas não secantes no outro lado em que os ângulos são maiores que
dois ângulos rectos, pelo que as linhas rectas serão não secantes em ambos os
lados; e se assim for, elas são paralelas. Mas foi provado que a linha que cai
sobre paralelas fará os ângulos internos no mesmo lado iguais a dois ângulos
rectos. Os mesmos ângulos são por isso iguais a dois ângulos rectos e menores
que dois ângulos rectos, o que é impossível”
(Proclus,
séc V, 366.15-367.3)
|
Ptolomeu demonstrou que, nas condições
referidas, as rectas se intersectam. De seguida, completa a demonstração e prova que elas
se intersectam do lado em que a soma dos ângulos internos é menor que dois ângulos
rectos e não na direcção em que é maior:
|
“Sejam
AB e CD duas linhas rectas, e seja EFGH uma linha caída sobre elas que faz os
ângulos AFG e CGF menores que dois ângulos rectos. Por isso os outros ângulos
são maiores que dois ângulos rectos. Agora já foi demonstrado que as linhas
rectas não são não secantes. Mas se elas se encontram uma com a outra,
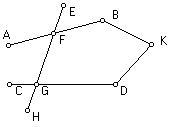
será
ou no lado de A e C ou no lado de B e D. Assumamos que elas se encontram no lado
de B e D no ponto K. Então como os ângulos AFG e CGF são menores que dois ângulos
rectos e os ângulos AFG e BFG são iguais a dois ângulos rectos, se o termo
comum, o ângulo AFG, é subtraído, o ângulo CGF será menor que o ângulo BFG.
Segue-se que o ângulo externo do triângulo KFG é menor que o interno oposto,
o que é impossível. Consequentemente elas não se encontram neste lado. Mas
elas encontram-se. Portanto elas encontram-se no outro lado, naquele em que os
ângulos são menores que dois ângulos rectos.”
(Proclus,
séc. V, 367.12-367.27)
|
E assim termina a demonstração de Ptolomeu do quinto postulado de
Euclides. Ou melhor, são estes os trechos da demonstração de Ptolomeu que
chegaram até nós. Porque estes trechos são transcrições feitas por
Proclus da obra de Ptolomeu, não podemos saber ao certo se Proclus terá
reproduzido com exactidão a argumentação de Ptolomeu. Resta-nos acreditar nas
palavras de Proclus que declara citar Ptolomeu na totalidade das três demonstrações apresentadas.
Topo


