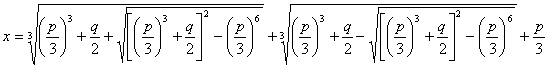| A “Ars Magna”, escrita em latim, é o primeiro grande tratado exclusivamente dedicado à álgebra. Nessa obra, Cardano trata a resolução de variadíssimas equações, indicando métodos cuja prova põe à disposição do leitor. No que respeita à resolução da cúbica, desde o capítulo decimo primeiro ao capítulo vigésimo terceiro são minuciosamente estudados treze tipos de equações, pela ordem seguinte: |  |
|
|
||
Observe-se que a necessidade de tratamento de todos estes casos, que se deve ao facto de apenas serem admitidos coeficientes positivos, torna a leitura do livro muito fastidiosa para o leitor actual.
No início do capítulo onze antes de tratar da equação ![]() , Cardano referiu que a invenção do método da resolução da
cúbica se ficou a dever a Scipione del Ferro e que foi através de
Tartaglia
que tomou conhecimento da fórmula de resolução. Em seguida, reconhecendo a
dificuldade da tarefa em que se empenhavam, começou a demonstração.
, Cardano referiu que a invenção do método da resolução da
cúbica se ficou a dever a Scipione del Ferro e que foi através de
Tartaglia
que tomou conhecimento da fórmula de resolução. Em seguida, reconhecendo a
dificuldade da tarefa em que se empenhavam, começou a demonstração.
A metodologia utilizada por Cardano em cada um dos treze capítulos atrás mencionados é a seguinte: primeiro faz a demonstração para um caso particular, utilizando, quase sempre relações entre volumes de cubos e paralelepípedos já estabelecidos em capítulos anteriores, em seguida, enuncia a regra geral para todas as equações do mesmo tipo, por fim, aplica a regra a alguns exemplos numéricos, acompanhando-a de uma breve explicação.
Assim, no estudo da cúbica ![]() , considera o caso particular
, considera o caso particular ![]() (isto é,
(isto é, ![]() e
e ![]() ) e começa a demonstração com as palavras:
) e começa a demonstração com as palavras:
Por exemplo, seja 6H3 mais seis vezes o seu lado 6H igual a 20, e sejam AE e CL dois cubos cuja diferença é 20 e tais que o produto de AC, o [de um] e CK, o lado [do outro], é 2, nomeadamente um terço do coeficiente de x (...) (Cardano, 1993, p.96)
Em linguagem actual isto significa que vai tomar um cubo de lado
a e um cubo de lado b tais que a diferença entre os volumes é
20, isto é,![]() e o produto dos comprimentos dos lados é 2, ou seja,
e o produto dos comprimentos dos lados é 2, ou seja, ![]() .
.
A justificação, apresentada de forma retórica e baseada em argumentos geométricos, consiste resumidamente no seguinte:
Como ![]() e
e ![]() vem:
vem: ![]() . Por um resultado (Cardano, 1993, cap VI),
. Por um resultado (Cardano, 1993, cap VI), ![]() . Logo,
. Logo, ![]() , isto é
, isto é ![]() é solução da equação
é solução da equação ![]() .
.
A formulação da regra geral para a resolução da equação ![]() é, então dada do seguinte modo: torna-se o cubo da terça
parte do número de lados, isto é, um terço do coeficiente de x; soma-se-lhe o
quadrado de metade da constante da equação, e toma-se a raiz quadrada do
total. Faz-se isto duas vezes; a uma das duas soma-se metade do número que já
se quadrou e à outra subtrai-se metade do mesmo. Tem-se o que Cardano
chama um
binómio e o seu apótema, terminologia usada por Euclides no
livro X dos elementos. Então, subtrai-se a raiz cúbica do apótema da
raiz cúbica do binómio, obtendo-se o lado pretendido.
é, então dada do seguinte modo: torna-se o cubo da terça
parte do número de lados, isto é, um terço do coeficiente de x; soma-se-lhe o
quadrado de metade da constante da equação, e toma-se a raiz quadrada do
total. Faz-se isto duas vezes; a uma das duas soma-se metade do número que já
se quadrou e à outra subtrai-se metade do mesmo. Tem-se o que Cardano
chama um
binómio e o seu apótema, terminologia usada por Euclides no
livro X dos elementos. Então, subtrai-se a raiz cúbica do apótema da
raiz cúbica do binómio, obtendo-se o lado pretendido.
Observe-se que, os números ![]() e
e ![]() procurados são as raízes da equação
procurados são as raízes da equação ![]() ,
isto é são
,
isto é são ![]() e
e ![]() .
.
Logo, a única raiz real da cúbica ![]() , com p e q positivos, é:
, com p e q positivos, é:
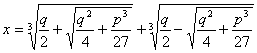
Exemplo:
A aplicação desta regra à resolução da equação ![]() permite obter imediatamente a solução, pois:
permite obter imediatamente a solução, pois:
O cubo da terça parte do coeficiente de x é 8, o quadrado de
metade da constante é 100, a raiz quadrada do todo é ![]() , somando a 10 a uma das parcelas obtém-se o binómio
, somando a 10 a uma das parcelas obtém-se o binómio
![]() e subtraindo 10 à outra parcela obtém-se o apótema
e subtraindo 10 à outra parcela obtém-se o apótema
![]() , a solução
é:
, a solução
é: ![]() .
.
A resolução destas equações seguiu-se a das equações ![]() e
e ![]() . Para estes dois tipos em que também não estava presente o
termo quadrático, Cardano indicou a solução,
. Para estes dois tipos em que também não estava presente o
termo quadrático, Cardano indicou a solução,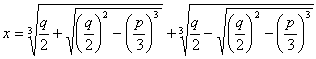 e, não
obstante ter tido a
preocupação de resolver os outros tipos de cúbicas
(1) que já
referimos, acabou por mostrar que qualquer dessas equações se podia
transformar numa equação onde não figurava o termo de grau dois.
e, não
obstante ter tido a
preocupação de resolver os outros tipos de cúbicas
(1) que já
referimos, acabou por mostrar que qualquer dessas equações se podia
transformar numa equação onde não figurava o termo de grau dois.
Não registaremos todas as considerações feitas por Cardano
para
reduzir uma cúbica qualquer a outra onde o termo de grau dois estivesse
ausente. No entanto pode constatar-se que, nas reduções que efectuou, usou
substituições dos tipos ![]() e
e ![]() .
.
Assim, por exemplo, para reduzir a cúbica ![]() a outra cúbica que não tivesse termo de grau dois, um dos
procedimentos que propôs foi: substituir x por
a outra cúbica que não tivesse termo de grau dois, um dos
procedimentos que propôs foi: substituir x por ![]() .
.
Na primeira equação cúbica tratada no Ars Magna, que era
do tipo ![]() , (p e q positivos), a fórmula antes indicada
por Tartaglia para obter a solução funciona sempre, pois, sendo p e
q positivos, é
, (p e q positivos), a fórmula antes indicada
por Tartaglia para obter a solução funciona sempre, pois, sendo p e
q positivos, é ![]() . No entanto, na segunda equação
. No entanto, na segunda equação
![]() e na terceira
e na terceira
![]() , (p e q positivos) tal não acontece.
, (p e q positivos) tal não acontece.
De facto, quando ![]() não tem significado em IR. Não
é, então, possível recorrer à fórmula indicada para obter as raízes – contudo
estas equações têm raízes, têm até três raízes reais, como já tinha sido
referido no primeiro capítulo do Ars Magna, o que parece ser
contraditório.
não tem significado em IR. Não
é, então, possível recorrer à fórmula indicada para obter as raízes – contudo
estas equações têm raízes, têm até três raízes reais, como já tinha sido
referido no primeiro capítulo do Ars Magna, o que parece ser
contraditório.
Foi certamente por observar esse facto que Cardano procurou contornar o problema, começando por supor, no enunciado da regra geral de resolução destas equações, que o cubo da terça parte do coeficiente de x não é maior do que o quadrado de metade da constante da equação. Contudo, não indicou, nesse capítulo, nenhuma alternativa que resolvesse a situação problemática.
No entanto, ainda no Ars Magna, mas num capítulo mais adiante, intitulado “Acerca de regras particulares e imperfeitas”, Cardano volta a referir-se a equações do tipo “cubo igual a primeira potência e constante”, enunciando algumas regras, que reconhece serem particulares, para a determinação de soluções.
E, usando precisamente o exemplo ![]() , que não está nas condições requeridas para a aplicação da
fórmula por ele proposta anteriormente, pois
, que não está nas condições requeridas para a aplicação da
fórmula por ele proposta anteriormente, pois ![]() resolve a equação do seguinte modo:
resolve a equação do seguinte modo:
Divide-se o coeficiente de x em duas partes tais que o produto de uma delas pela raiz quadrada da outra é 32. As partes são 16 e 4;
Soma à primeira destas partes um quarto da segunda, obtendo 16+1, ou seja 17;
Toma a raiz quadrada do todo, ![]() , e soma-lhe metade da raiz quadrada da segunda parte.
, e soma-lhe metade da raiz quadrada da segunda parte.
Obtém-se uma única solução, ![]() .
.
É fácil verificar que ![]() é, de
facto, a solução da equação
é, de
facto, a solução da equação ![]() .
.
Na primeira edição do Ars Magna,
Cardano não dá qualquer
justificação para este procedimento e é até curioso observar que para resolver
a equação ![]() , que é do tipo da anterior, ele propõe outro processo.
Divide o coeficiente de x em três partes proporcionais tais que o produto da
parte do meio pela soma das raízes das outras duas é igual a 30. As partes são
9, 6 e 4 e a solução é a soma das raízes das partes extremas. No entanto, na
edição de 1570, dá para o último caso de que falámos uma prova geométrica.
, que é do tipo da anterior, ele propõe outro processo.
Divide o coeficiente de x em três partes proporcionais tais que o produto da
parte do meio pela soma das raízes das outras duas é igual a 30. As partes são
9, 6 e 4 e a solução é a soma das raízes das partes extremas. No entanto, na
edição de 1570, dá para o último caso de que falámos uma prova geométrica.
(1)
Observe-se, a título de curiosidade, que para a equação ![]() , a solução apresentada era:
, a solução apresentada era: