O papiro de Berlim foi comprado em 1850, em Luxor, por A. H. Rhind - na mesma altura que o papiro de Rhind. Este papiro encontrava-se em muito mau estado sendo analisado e restaurado  50 anos mais tarde por Schack-Schackenburg. Encontra-se, actualmente, no Museu Staatliche em Berlim.  Neste papiro aparece pela primeira a solução de uma equação do 2º grau. Na verdade, o problema em seguida apresentado dá origem a um sistema de duas equações, sendo uma delas uma equação do 2º grau:

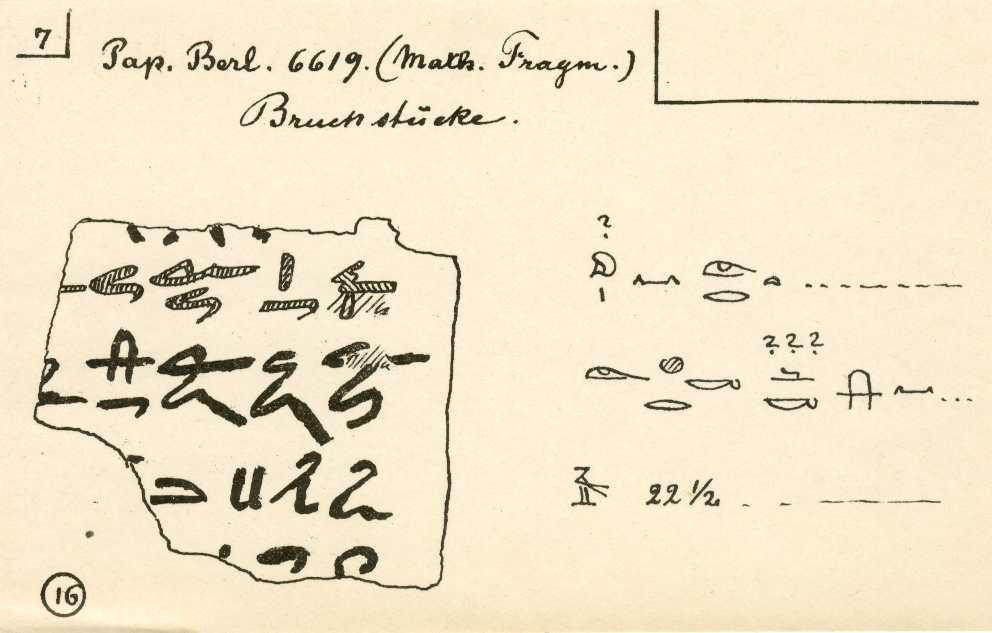Problema: Diz-se que a área de um quadrado de 100 meh quadrados é igual à soma das áreas de outros dois quadrados mais pequenos. O lado de um deles é 1/2+1/4 do outro. Qual o comprimento dos lados dos dois quadrados?

Suponha-se que um dos quadrados tem lado 1 meh. O lado do outro quadrado será, então, de  1/2+1/4 de meh. As áreas serão: para o primeiro 1 meh quadrado e para o segundo1/2+1/16 de meh quadrado. Então a soma das áreas dos dois quadrados é 1+1/2+1/16 de meh quadrado. A raiz  quadrada desta soma é 1+1/4. Como a raíz quadrada de 100 é 10 devemos encontrar um número N tal que multiplicado por 1+1/4 nos dê 10, ou seja, temos que dividir 10 por 1+1/4. Assim, N = 8. Portanto, x = 8 e y = (1/2+1/4).8 = 6, ou seja, um quadrado terá de lado 8 meh e o outro 6 meh.