![]()
|
O papiro de Moscovo, também conhecido por Golenishchev em homenagem ao egiptólogo que o comprou em 1893 no Egipto foi adquirido em 1917 pelo Museu de Belas Artes de Moscovo. Escrito em hierático por um escriba desconhecido cerca de 1850 a.C., as suas dimensões são, aproximadamente, 8 centímetros de largura por 5 metros de comprimento. Contém 25 problemas, sendo impossível interpretar muitos deles devido ao grau de degradação do manuscrito. Neste papiro é apresentada uma forma de cálculo do volume do tronco de pirâmide de base quadrada |
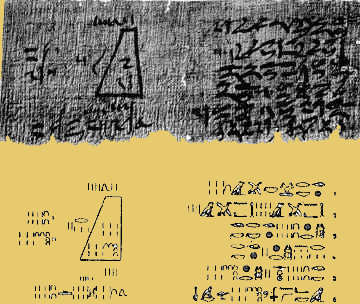 |
Problema: Um tronco de pirâmide tem 6 cúbitos de altura, 4 cúbitos de base por 2 cúbitos no topo. Qual o volume?
Os egípcios terão chegado à conhecida fórmula V = h(a² + b² + ab) / 3.