Procedimento para encontrar um ciclo euleriano de G
partindo de uma decomposição das arestas em ciclos disjuntos.
Seguindo a lista de regras abaixo construímos passo a passo
uma cadeia simples g que no fim resultará num ciclo euleriano.
Suponhamos que as arestas do grafo conexo G se decompõem nos seguintes
ciclos, disjuntos entre si:
c1 , c2 , ... cn.
- Orientem-se todos os ciclos ci .
- Selecione-se o ciclo c1 e uma sua aresta como primeiro
elemento de g .
- A cadeia g percorre o ciclo selecionado, no sentido fixado em 1., até que
uma das condições 4. ou 5. se verifique.
- Se a extremidade final de g incidir com um ciclo cj
disjunto das arestas de g selecionamos esse novo ciclo começando a percorrê-lo
a partir da extremidade final de g . Volte à regra 3. .
- Quando g tiver percorrido completamente o ciclo selecionado
ci volte ao penúltimo ciclo iniciado, mas não terminado, selecionando-o
de novo. A cadeia g volta a percorrer este ciclo. Siga para a regra 3. .
- Quando g terminar de percorrer o ciclo selecionado e não haja
mais ciclos por percorrer g é um ciclo euleriano.
Em cada passo g é uma cadeia euleriana.
No fim g é um ciclo euleriano.
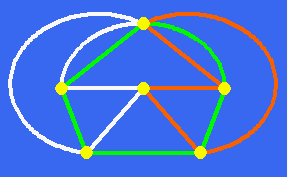
Verifique, no grafo da animação seguinte, decomposto nos três ciclos:
vermelho, verde e branco, a aplicação das regras acima.
Para correr a animação coloque o rato sobre a figura.
A animação pára sempre que afaste o rato da figura.