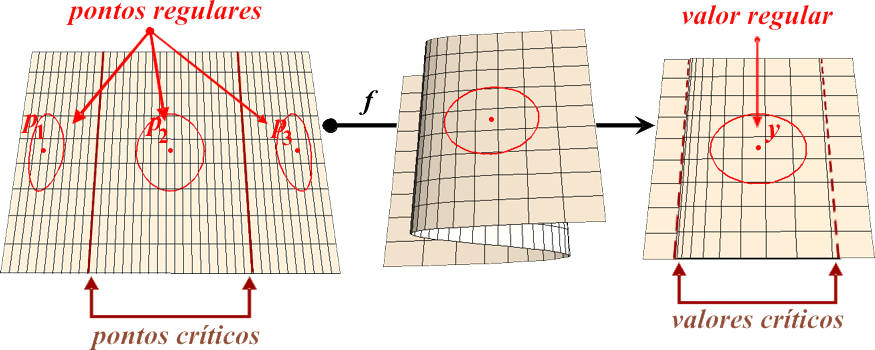
Pontos e Valores, Críticos e Regulares

Sejam $X$ e $Y$ variedades compactas orientadas sem bordo com $\dim(X) = \dim(Y)$.
Seja $f\colon X\to Y$ uma aplicação diferenciável.

Os elementos $p\in X$ são referidos como pontos do domínio de $f$.

Os elementos do contra-domínio $y\in f(X)\subseteq Y$ são referidos como valores de $f$.

Chama-se ponto crítico de $f$ a um ponto $p\in X$ tal que $\det(D f_p) = 0$.

$y\in Y$ diz-se um valor crítico de $f$ se $f^{-1}(y)$ contiver pelo menos um ponto crítico.

$y\in Y$ diz-se um valor regular de $f$ se $f^{-1}(y)$ não contiver nenhum ponto crítico.

Proposição
Se $y\in Y$ é um valor regular então $f^{-1}(y) =\{ p\in X\colon f(p)=y \}$ é um conjunto finito.

>> Definição Local de Grau