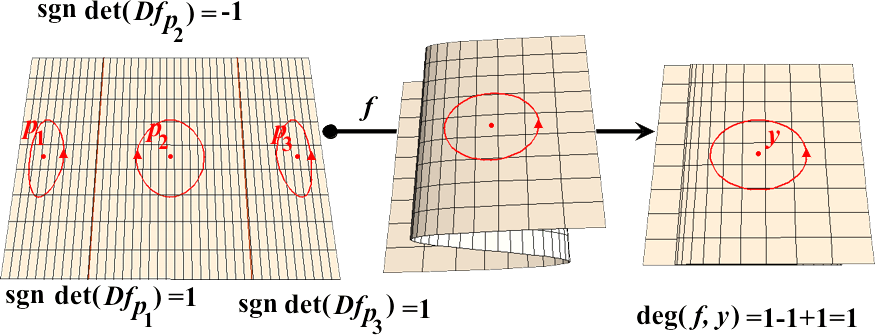
Definição Local de Grau
Sejam $X$ e $Y$
variedades compactas orientadas sem bordo da mesma dimensão, e
$\,f\colon X\to Y$
uma aplicação diferenciável.
Definição
Chama-se grau de $f$ num valor regular
$y\in Y$,
à soma
$$ {\rm deg}(f,y)= \sum_{p\in f^{-1}(y)} {\rm sgn}(\det D f_p) . $$
Proposição
Se a variedade $Y$ for conexa, todos os valores regulares de
$\,f\colon X\to Y$
têm o mesmo grau:
$${\rm deg}(f, y_1 ) =
{\rm deg}(f, y_2)$$
quaisquer que sejam os valores regulares
$y_1, y_2\in Y$ de $f$.
Definição
Chama-se grau de $f$
ao grau comum dos seus valores regulares
$$ {\rm deg}(f) = {\rm deg}(f,y) $$
qualquer que seja o valor regular $y\in Y$ de $f$.
>> Propriedades Globais do Grau
>> Mapas entre Superfícies