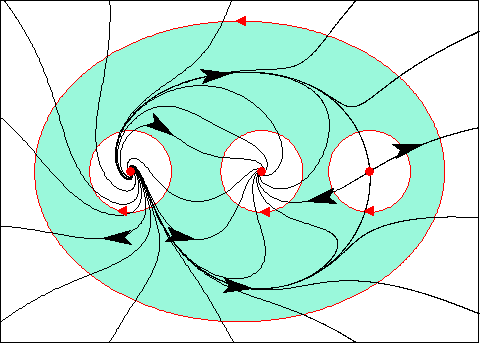
Prova do Lema de Hopf

Sejam $\{p_i\}_i$ as singularidadedes do campo $\xi$,
$\{D_i\}_i$ discos disjuntos centrados nas singularidades $\{p_i\}_i$,
$C_i^+ =\partial D_i$ com a orientação positiva,
$C_i^- =\partial D_i$ com a orientação oposta,
$Z=X\setminus \cup_i D_i$.   Então $\partial Z = \partial X \cup (\cup_i C_i^-)$.

A aplicação $f\colon \partial X \to \mathbb{S}^{n-1} $, $\;f(x)=\xi(x)/\|\xi(x)\| $ estende-se a $Z$. Logo, pela proposição seguinte, $\mathrm{deg}(f\vert_{\partial Z})=0$.
Como a aplicação de Gauss $g$ é homotópica a $f\vert_{\partial X}$, \begin{align*} \mathrm{deg}(g) &= \mathrm{deg}(f\vert_{\partial X}) = \mathrm{deg}(f\vert_{\partial Z}) - \sum_i \mathrm{deg}(f\vert_{C_i^-})\\ &= \sum_i \mathrm{deg}(f\vert_{C_i^+}) = \sum_i \mathrm{Ind}_x(\xi) . \end{align*}

Proposição
Sejam $Z$ e $Y$ variedades orientadas compactas,
$Y$ sem bordo e $Z$ com bordo, tais que $\dim(Z) = \dim(Y) +1$.
Seja $f\colon Z\to Y$ uma aplicação diferenciável.
Então $\; \mathrm{deg}(f\vert_{\partial Z})=0 $.

>> Teorema de Poincaré Hopf