e $\xi$ um campo vectorial em $X$.
Chama-se singularidade de $\xi$ a um zero de $\xi$,
i.e., um ponto $p\in X$ tal que $\xi(p)=0$.
Uma singularidade $p\in X$ diz-se isolada se
$p$ fôr o único zero de $\xi$ numa vizinhança de $p$.
Definição
Seja $p$ uma singularidade isolada de $\xi$.
Chama-se índice de $\xi$ em $p$ ao número inteiro
$$ {\rm Ind}_p(\xi) = {\rm deg}(f) , $$ onde$f \colon \mathbb{D}\to \mathbb{S}^{n-1}$, $\; f(x)= \xi(x)/\|\xi(x)\| $,
$n = \dim(X)\, $ e $\,\mathbb{D}$ é um disco centrado em $p$,
que não contém nenhuma outra singularidade de $\xi$.
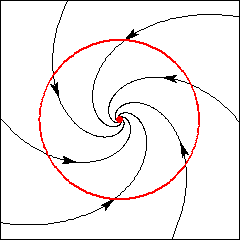
Poço (atractor): Índice 1.
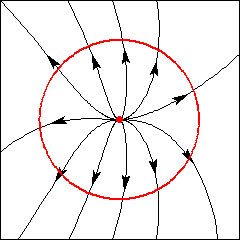
Fonte (repulsor): Índice 1.
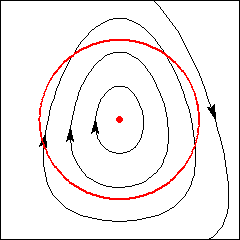
Centro: Índice 1.
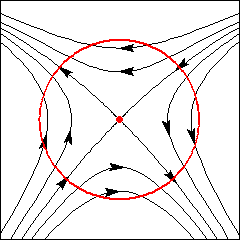
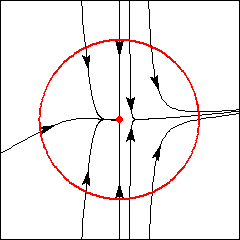
Sela: Índice -1.
Sela-nó: Índice 0.
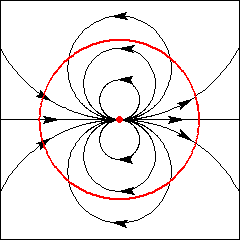
Singularidade degenerada com índice 2.
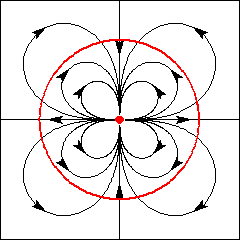
Singularidade degenerada com índice 3.
>> Teorema de Poincaré Hopf