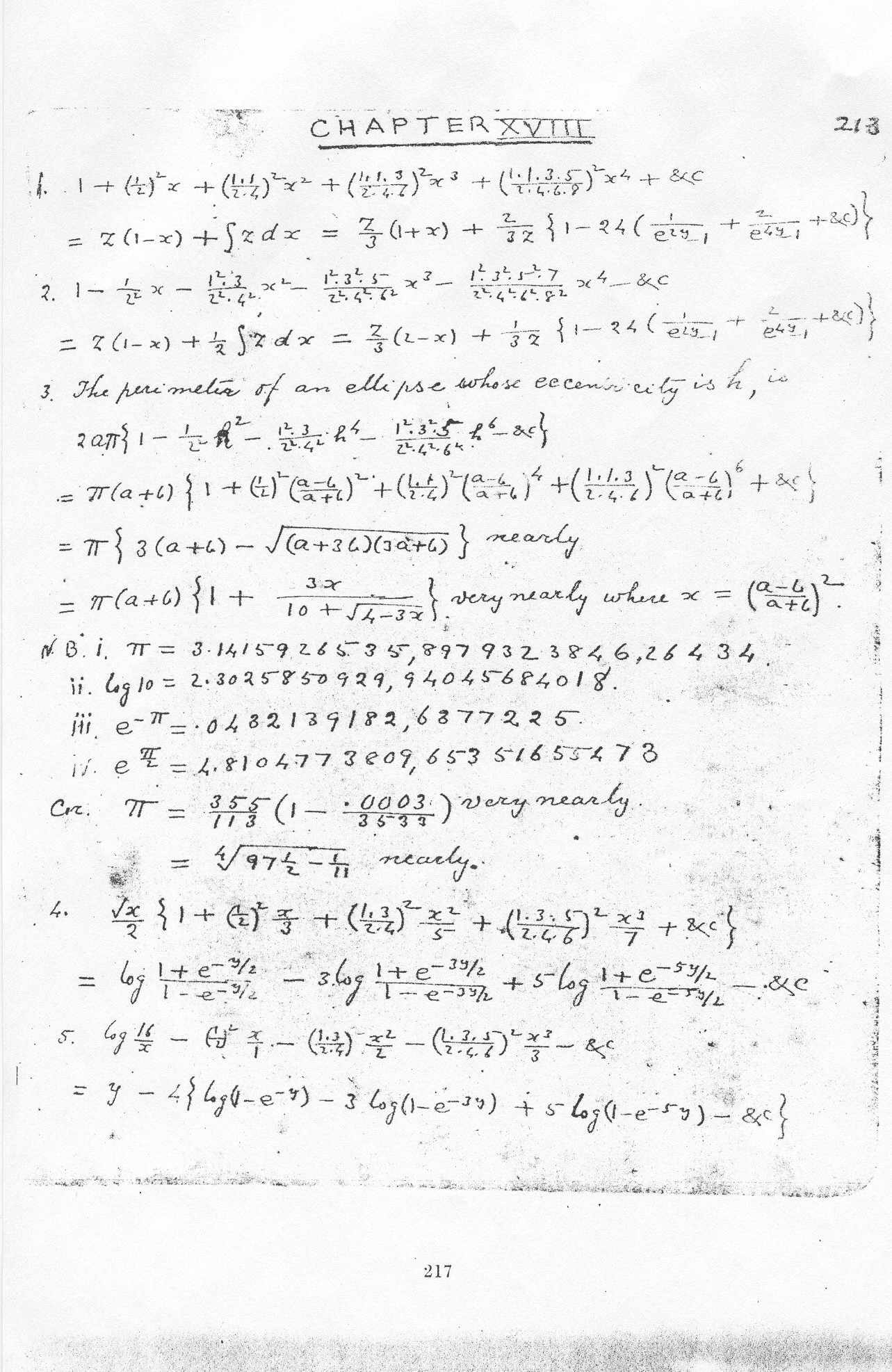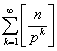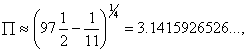|
Introdução
Para celebrar o
centenário do nascimento de Ramanujan, em Junho de 1987, foi organizada uma
conferência na Universidade de Ilinois em Urbana-Champaign. Numerosos caminhos
e vários cenários permitiram reunir pesquisas dos artigos,
problemas, cartas, blocos de notas e manuscritos não publicados de Ramanujan
numa panóplia de áreas de investigação, incluindo “inúteis” funções
teta, mecânica estatística, álgebras de lie, teoria probabilística de números,
formas modelares, funções elípticas, multiplicações complexas, séries
hipergeométricas, q-series, expansões assimptóticas e integrais beta. Muitos
outros matemáticos de nome não conseguiram ter tanto impacto em investigação
matemática. Apesar de muitos dos resultados apresentados na conferência terem
sido entendidos e apreciados por matemáticos que fazem investigação fora
desta área, esta era uma conferência para génios.
Muitas
das belas descobertas de Ramanujan são, contudo, fáceis de compreender,
elementares e apelam a uma grande variedade de gostos. Assim este artigo é
essencialmente publicado para gente vulgar, com limitadas preocupações
intelectuais. A maior parte dos teoremas aqui referidos, necessitam de uma álgebra
elementar, para serem demonstrados. A maioria deles pode ser encontrado numa
parte ainda desorganizada do livro de notas II, que se compilou como terceiro
livro de notas de Ramanujan, que os publicou para os habituais leitores do Journal
of the Indian Mathematical Society. Os resultados que vamos descrever vão
ao mais profundo da álgebra elementar, da igualdade de séries de potências e
da teoria elementar dos números.
Concluímos
o nosso artigo com algumas aproximações do número π.
Muitas referências vão ser feitas aos dois
volumes de notas de Ramanujan. O segundo volume contém o segundo e terceiro
livros de notas e todos os números das páginas neste artigo referem-se à
paginação neste segundo volume.
Teoria
dos números
Suponhamos
que p é um número primo e n é um inteiro positivo. Assim, por um teorema
bastante conhecido da Teoria Elementar dos Números, a maior potência de p que
divide n! é igual
a
Apesar
de, ao longo dos anos, este teorema ter sido bastante usado pelos investigadores da
teoria dos números, as desigualdades
 |
(4.1)
|
dadas por Ramanujan
no seu terceiro “notebook”, parecem não ter sido devidamente consideradas até hoje. Ambas
as desigualdades em (4.1) são exactas. Se
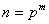 para algum m inteiro positivo, um cálculo
elementar mostra que
. Por outro lado, se para algum m inteiro positivo, um cálculo
elementar mostra que
. Por outro lado, se
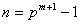 , por um cálculo directo e tendo em conta
, por um cálculo directo e tendo em conta
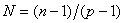 que que
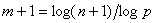 ,
,
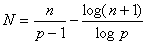 . .
Na realidade,
Ramanujan declarou (4.1) com o p substituído por um
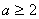 inteiro positivo.
inteiro positivo.
Bhargava, Adiga e
Somashekara deram uma demonstração de (4.1) quando p é um inteiro positivo
excedendo 1. Damos agora outra demonstração.
Demonstração
de (4.1): Primeiro, escrevendo n em
função de p, i.e., estabelecendo

encontramos, depois
de um simples cálculo, que
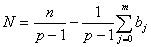 |
(4.2)
|
donde sai a segunda
desigualdade de (4.1).
A primeira desigualdade de
(4.1) é bastante mais difícil de estabelecer.
Estamos muito gratos a
B.Reznick por nos ter fornecido a seguinte demonstração.
Seja
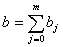 . .
Então, por (4.2),
é suficiente provar que
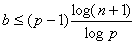 |
(4.3)
|
Escrevendo
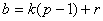 |
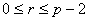 |
(4.4)
|
Então
Segue-se que
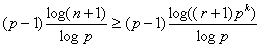 |
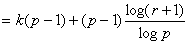 |
(4.5)
|
Por (4.3)-(4.5),
devemos conseguir terminar a demonstração se mostrarmos que
|
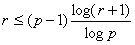 |
(4.6)
|
Primeiro, se r=0,
(4.6) claramente verifica a igualdade.
Se r
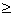 1, (4.6) pode ser escrita na forma
1, (4.6) pode ser escrita na forma
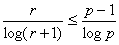 , ,
ou
|
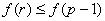 |
(4.7)
|
onde
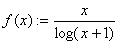 . . |
No entanto, por cálculos
elementares, verifica-se que
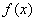 é válida para qualquer
é válida para qualquer
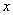 inteiro positivo.
inteiro positivo.
Desde que
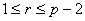 , (4.7) também é válido quando a desigualdade é estrita, e assim terminamos
a demonstração.
, (4.7) também é válido quando a desigualdade é estrita, e assim terminamos
a demonstração.
Como referido na introdução,
concluímos esta pequena amostra das descobertas elementares do Ramanujan com
uma nota do
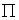 . As fracções continuas dão-nos uma excelente aproximação racional do
. As fracções continuas dão-nos uma excelente aproximação racional do
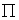 .
.
Assim, esta simples fracção continua
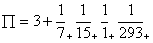 …
…
dá-nos sucessivas
aproximações
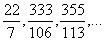 . Repare que
. Repare que
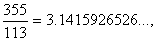
que equivale à
expansão decimal do
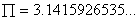 através de 6 casas decimais. O
aparecimento de um “grande” quarto quociente parcial, 293, é o primeiro
responsável por este sucesso.
através de 6 casas decimais. O
aparecimento de um “grande” quarto quociente parcial, 293, é o primeiro
responsável por este sucesso.
Retirando uma breve diversão
do seu famoso apontamento nas aproximações do
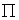 [24], [27, p.35], Ramanujan oferece
a aproximação
[24], [27, p.35], Ramanujan oferece
a aproximação
|
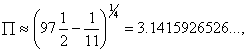 |
(4.8)
|
a qual, “foi
obtida empiricamente”.
Como é que Ramanujan terá deduzido esta
aproximação tão pouco usual, aproximação que pode ser encontrada no seu 2º e 3º notebooks [26, pp.217,
375]?
N.D. Mermin [16], [17, pp. 304-305] ofereceu a melhor explicação para a
aproximação de Ramanujan (4.8).
Na expansão decimal de
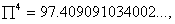 observe-se que o par de dígitos 09
aparece duas vezes na sucessão, seguido do par 10, que é próximo ao 09.
Assim,
observe-se que o par de dígitos 09
aparece duas vezes na sucessão, seguido do par 10, que é próximo ao 09.
Assim,
é a aproximação
natural do
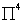 .
.
A facilidade
que Ramanujan detém para com as fracções continuas é inigualável na história matemática, e como tal
deve ter observado que [16], [17], [4, p.151]
Truncando
esta fracção continua mesmo antes do “maior” quociente parcial 16,539 dá
a aproximação (4.8).
|