Embora a relação entre Barrow e Newton tenha sido sempre um mistério, sabe-se que durante 1664/5, Barrow deu em Cambridge um ciclo de aulas que abordavam problemas sobre espaço, tempo e movimento, às quais Newton assistiu. Sabe-se também que a cópia dos Elementos de Euclides publicada por Barrow em 1665 foi estudada cuidadosamente por Newton. Além disso, Barrow possuía uma boa biblioteca e provavelmente emprestava e recomendava livros a Newton prática decisiva numa época em que existiam poucos livros de texto destinados aos alunos e por isso para aprender era necessário estudar com os mestres.
Por outro lado, Newton conhecia os trabalhos de Wallis de 1675. De facto, Newton reconheceu que foi conduzido às suas descobertas iniciais em análise pelo Arithmetica infinitorum de Wallis e que os princípios de indução e de interpolação que este utilizava podiam também ter sido importantes para a sua descoberta do teorema do binómio. O conceito newtoniano de número - razão abstracta entra duas quantidades e não colecção de unidades - está mais próximo do de Wallis do que de Barrow.
Segundo Boyer (1959) outro elemento adicional do método das fluxões de Newton era o uso das séries infinitas. Os filósofos da escolástica já tinham estudado séries infinitas em ligação com a representação geométrica da variabilidade e Gregory de St. Vincent (1584-1667), Tacquet (1612-1660) e Fermat (1601-1665) tinham já feito uso das progressões infinitas. Contudo, as primeiras investigações sobre séries aritméticas infinitas em geral foram trabalho de matemáticos ingleses tais como Wallis (1616-1703) e James Gregory (1638-1675). O uso destas séries era, de facto, responsável pela universalidade das aplicações do método das fluxões libertando-o dos preconceitos geométricos.
Newton estava na posse do seu cálculo das fluxões em 1665/66, isto é, por volta da época em que assista às lições de Barrow e tinha já descoberto o teorema binomial. Contudo, a primeira exposição do cálculo surgiu apenas em 1669 no De analysi per aequationes numero terminorum infinitas. O trabalho só foi publicado em 1711 mas circulou entre os seus amigos. Nesta monografia Newton não fez uso explicito das suas ideias sobre fluxões nem das suas notações. Em vez disso usou os infinitamente pequenos tanto de maneira geométrica como analítica, à semelhança do que se pode encontrar em Barrow e Fermat, estendendo a sua aplicabilidade através do uso do teorema do binómio. Neste texto Newton emprega a ideia de rectângulo indefinidamente pequeno ou "momento" de área e encontra a quadratura da curva da seguinte maneira:
Seja a curva desenhada de maneira a que à abcissa x e ordenada y a área seja dada por
Segundo a notação de James Gregory seja o o momento ou incremento infinitesimal da abcissa. A nova abcissa será então x+o e a área aumentará
A esta expressão aplicamos o teorema do binómio, dividimos por o e desprezamos todos os termos que ainda tenham o, o resultado será então
Isto é, se a área é dada por
a curva será dada por
.
Reciprocamente, se a curva for
a área será
.
Trata-se de uma expressão para a área a que Newton chegou, não através da determinação de uma soma de áreas infinitesimais nem através de métodos equivalentes empregues pelos seus antecessores, mas por consideração do aumento momentâneo da área no ponto em questão. Por outras palavras, enquanto as quadraturas tinham previamente sido determinadas por meio do equivalente do integral definido, tomado como sendo o limite da soma, Newton determina primeiro a taxa de variação da área e daqui a área propriamente dita através daquilo que actualmente chamamos o integral indefinido da função que representa a ordenada. Para além disso é de notar que o processo que é tornado fundamental nesta proposição é o da determinação de taxas de variação. Por outras palavras, aquilo que nós chamamos actualmente de derivada é tomada como ideia básica e o integral é definido em termos desta.
Desde Torricelli (1608-1647) a Barrow (1630-1677) que já era conhecida a relação entre derivada e integral. Mas Newton foi o primeiro a dar um procedimento geral, aplicável para determinar a taxa de variação instantânea e para invertê-la no caso de problemas envolvendo somas. Anteriormente, a tendência tinha sido sempre na direcção contrária - reduzir os problemas sempre que possível à determinação de quadraturas. Em geral é com este passo dado por Newton que se considera que o cálculo nasce.
Newton aplicou o seu método para calcular a quadratura de várias outras curvas
e 
.
Alguns anos mais tarde, ao mandar estes resultados a Collins (1625-1683), descreve também um número de proposições sobre máximos e mínimos e sobre tangentes, que ele tinha obtido usando os seus métodos. Esta carta escrita a Collins em 10 de Dezembro de 1672 tornar-se-ia importante para a controvérsia com Leibniz sobre a prioridade da descoberta do cálculo. Nessa carta, Newton confessa claramente que as suas regras são semelhantes às de Sluse (1622-1685) e Hudde (1633-1704) ainda que mais gerais. Mais à frente admite que foi buscar inspiração ao método de Fermat melhorado por Gregory e Barrow. A mudança do E de Fermat para o de Gregory e Newton é trivial. O significado do trabalho de Newton reside em primeiro lugar no facto de que ele aplica o método "directamente e inversamente", nas suas próprias palavras. Em segundo lugar, Newton considera-o, relativamente ao uso das séries infinitas, como um algoritmo universal enquanto o método de Fermat, bem como as modificações deste operadas por Sluse, Hudde e Huygens, era só aplicável ao caso das funções algébricas racionais.
É de notar que apesar do trabalho de Newton conter os procedimentos essenciais do cálculo, a sua justificação destes não é clara. Newton não explica porque razão se desprezam os termos que envolvem potências de o, tal como Fermat não justificava a omissão das potências de E ou Barrow a omissão das potências de e e a. O seu contributo foi o de facilitar as operações e não o de clarificar os conceitos.
Na sua demonstração de que a área de
é dada por
podemos contudo obter pistas sobre a sua maneira de pensar. A ordenada y parece representar a velocidade a que a área aumenta enquanto a abcissa representa o tempo. O produto da ordenada por um pequeno intervalo na base dará uma pequena porção de área e a área total abaixo da curva consiste na soma de todos esses momentos de área. Esta é precisamente a concepção infinitesimal de Oresme (1323-1382), Galileu (), Descartes (1596-1650) com a diferença que estes tinham determinado a área total através da adição destes elementos infinitesimais, enquanto Newton determinou essa área a partir da sua taxa de variação num ponto.
Não é possível descrever com exactidão de que maneira Newton pensava nesta taxa de variação instantânea, mas provavelmente aceitava-a de maneira semelhante á concepção de velocidade que Galileu tinha tornado tão familiar mas não tinha definido rigorosamente. Um empirista como Newton, para quem a matemática era um método mais do que uma explicação, considerava aparentemente qualquer tentativa de questionar a instantaneidade do movimento como senso metafísica e por isso evitava defini-la. Contudo aceitava esta noção e fez dela a base da sua segunda e mais extensa exposição do cálculo, o Methodus fluxionum et serierum infinitarum, escrita em 1671 mas publicada apenas em 1736.
Boyer (1959) refere que é neste livro
que Newton introduz as suas notações características. Aqui ele
considera as suas quantidades variáveis como sendo geradas pelo movimento
contínuo de pontos, linhas e planos em vez de como agregados de elementos
infinitesimais - o ponto de vista que tinha aparecido na sua anterior monografia
De analysi. Este conceito de movimento para Newton é de tal maneira
intuitivo que nenhuma definição lhe pareceu necessária. À taxa de geração
ele chamava fluxão, designando-a por meio de uma letra com um ponto por
cima; à quantidade gerada chamava fluente empregando assim termos
utilizados anteriormente. Assim se x e y
são os fluentes então as suas fluxões são 
e
. Noutros sítios
Newton refere também que se podem considerar as fluxões
e e como novos fluentes
cujas fluxões são representadas por
e
e assim por diante. Os fluentes dos quais x e y
são as fluxões, representava-os Newton por 
e 
, os fluentes dos quais estas últimas quantidades eram as fluxões
escreviam-se como
e
e assim sucessivamente.
No Methodus
fluxiorum Newton afirma claramente o problema fundamental do cálculo: dada
a relação entre quantidades, encontrar a relação entre as fluxões destas e
reciprocamente. Em conformidade com este problema, dá então exemplos do
seu método. Estes exemplos podem ser representados pela determinação da
fluxão de 
; O seu tratamento deste caso difere ligeiramente da sua
anterior exposição no De analysi. Se o é um intervalo de
tempo infinitamente pequeno, então 
e
serão
incrementos indefinidamente pequenos, ou momentos, das quantidades fluentes x
e y. Substitui-se então x por 
e y por
na expressão como
anteriormente, expande-se esta expressão pelo teorema do binómio, corta-se os
termos que não contém o e divide-se por o. Como, para além
disso, o é suposto ser infinitamente pequeno, os termos que o contêm,
isto é, os momentos das quantidades podem ser tomados como zero em comparação
com os outros e, portanto, desprezados.
O
resultado, 
é
evidentemente o mesmo que obteve no De analysi sem usar fluxões. É
de notar que a introdução aqui do conceito de fluxão não é uma
modificação essencial do trabalho anterior. O infinitamente pequeno entra aqui
tão persistentemente como na exposição de 1669, mas da forma dinâmica do momento
de Galileu ou do conatus de Hobbes (1588-1679), em vez da forma estática do indivisível
de Cavalieri (1598-1647). Isto serve apenas à intuição para remover o freio (tal como
Newton o expressou) da doutrina dos indivisíveis. Em pensamento a
justificação para desprezar os termos infinitamente pequenos é para ser
feita precisamente na mesma base, sejam esses termos escritos como E, e,
a, o ou
. O
próprio Newton pareceu sentir aqui alguma necessidade para o conceito de limite,
pois frisou que as fluxões não se deviam considerar nunca isoladamente, mas
sempre em razão. Mais tarde, quando Newton procurou escapar das garras do
infinitamente pequeno, vai dar mais ênfase a este facto.
O terceiro estádio do seu pensamento aparece claramente no De quadratura
curvarum escrito em 1676 mas só publicado em 1704. Neste tratado Newton
procura remover todos os traços do infinitamente pequeno. As quantidades
matemáticas não eram consideradas como sendo feitas de momentos ou partes
muito pequenas mas como sendo descritas por um movimento contínuo. Para
determinar a fluxão de
Newton
procede como no Methodus fluxiorum substituindo x por x+o
tomando a fluxão de x como unidade. Expandindo
pelo
teorema do binómio e subtraindo
o
resultado é a variação que
corresponde à variação o em x, mas, agora, em vez de completar o
argumento por meio de um desprezo de termos de justificação duvidosa, Newton
forma a razão entre a variação em x e a variação em
, isto
é,
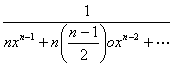
e aqui ele permite que o se aproxime de zero. A razão resultante é
a que chamaríamos hoje o limite da razão entre as variações e que Newton chama a razão última. Esta é também a razão das fluxões no ponto em questão
De notar que Newton escreve estas razões da maneira inversa à que se pratica actualmente.
A formação da razão de variação na variável independente e na função, e, finalmente, a determinação do limite quando a variação se aproxima de zero. No entanto, existem alguns elementos no pensamento de Newton que entretanto já não se consideram actualmente: o seu uso do tempo como variável independente auxiliar independente auxiliar é hoje em dia considerada inútil e a razão limite é a agora considerada simplesmente como um número em vez de como o quociente de duas taxas de variação. Se Newton tivesse dedicado mais tempo a clarificar o seu pensamento sobre as demonstrações por razões últimas, o cálculo podia ter sido estabelecido sobre o conceito de derivada um século antes de Cauchy. Com efeito, Newton sugere este tipo de argumento, mas, infelizmente, nas suas ilustrações do método das fluxões ele retoma a terminologia infinitesimal dos seus trabalhos anteriores.
De acordo com o que ele escreve no De quadratura, a sua descoberta do cálculo data de 1665/66. Como vimos, na década seguinte Newton vai escrever três relatos dos seus métodos mas não publica nada. Por volta de 1676 toma conhecimento que Leibniz estava a trabalhar em problemas semelhantes e em 24 de Outubro desse ano envia-lhe uma carta donde consta sobre a forma de anagrama uma afirmação sobre o problema fundamental do cálculo. Isto parece ter sido o seu único esforço para afirmar a sua prioridade na invenção do cálculo. Esse anagrama dizia: "dada numa equação os fluentes de qualquer número de quantidades, determinar as fluxões e vice versa" (cit in Boyer, 1959, p. 194) uma afirmação semelhante às que ele já tinha feito no seu Methodus fluxiorum e no De quadratura, que ele já tinha escrito, mas não publicado por esta altura. Nesta carta reconhece também a sua dívida para com Wallis, James Gregory, Sluse e outros mas não dá nenhuma exposição dos seus métodos. O primeiro relato publico do seu cálculo aparece de certo modo acidentalmente mais de dez anos depois no seu famoso Principia mathematica philosophiae naturalis em 1687. Neste livro as proposições dizem respeito a velocidades, acelerações, tangentes e curvaturas com as quais se lida hoje com os métodos do cálculo. Contudo, Newton demonstra-as usando geometria sintética quase sem efectuar nenhum tipo de cálculo analítico, ainda que em vários pontos deste trabalho ele dê indicações de um ponto de vista mais geral.
Numa série de lemas no seu primeiro livro (os Principia foram publicados em três volumes) ele expressa o tipo de argumentos que aparecem no De quadratura. "Quantidades e as razões de quantidades, que em qualquer tempo finito convergem de maneira continua para a igualdade e que antes do fim desse tempo se aproximam uma da outra que qualquer diferença dada, tornam-se ultimamente iguais."(cit in Boyer, 1959, p. 197). Evidentemente este é o tipo de proposição sobre limites com que Stevin, Valerio, Gregory de St. Vincent, Tacquet, Wallis e outros tentaram substituir o método Grego da exaustão. A visão de Newton de limite, tal como a destes filósofos naturais anteriores derivava de intuições geométricas que o levavam a fazer afirmações vagas e ambíguas como por exemplo "A razão última do arco, corda, tangente, qualquer uma de qualquer outra, é a razão da igualdade" e mais tarde fala da semelhança das "formas últimas de triângulos evanescentes."
De acordo com Boyer (1959) estas afirmações parecem implicar que Newton não estava a raciocinar aritmeticamente, como fazemos agora. O limite da sucessão de números representam as razões dos comprimentos das quantidades geométricas em questão, quando estas se tornam indefinidamente pequenas. Newton também era influenciado pelo ponto de vista infinitesimal do século XVII pensando em indivisíveis geométricos últimos. É verdade que ele nunca usou expressões como arcos, cordas, tangentes ou triângulos últimos mas apenas razões e formas últimas, expressões que permitem interpretações abstractas correctas e rigorosas, mas que sugerem fortemente outras interpretações em termos do ponto de vista mais atractivo dos infinitesimais. Que Newton compreendia as dificuldades envolvidas na visão ingénua dos infinitesimais é indicado na sua afirmação dos Principia que "Razões últimas em que as quantidades se anulam não são, estritamente falando, razões de quantidades últimas mas limites para os quais as razões dessas quantidades, decrescentes sem limite, se aproximam e ainda que se aproximem mais do que qualquer diferença dada, elas não podem nem ultrapassar nem ficar aquém antes de as quantidades terem diminuído indefinidamente." (cit in Boyer, 1959, p. 198). Esta é a afirmação mais clara que Newton dá em relação á natureza das razões últimas; e continua esta argumentação num lema do livro segundo dos seus Principia. De novo a sua exposição se torna dependente da ideia de quantidades infinitamente pequenas. É precisamente esta falta de claridade que conduzirá, no século seguinte, a discussões controversas, não só sobre a validade das fluxões de Newton, mas também sobre o que Newton realmente queria dizer com as afirmações anteriores e outras semelhantes.
Os Principia estão escritos no estilo da velha geometria sintética; por
isso, as referências ao método das fluxões são pouco numerosas. contudo no
segundo livro aparece pela primeira vez o fundamento desse método geral. Neste livro pode encontrar-se, como um lema, o princípio
fundamental, "O momento de qualquer genitum é igual aos momentos de cada
um dos lados gerados multiplicados pelos índices das potências desse lados e
pelos seus coeficientes continuamente."(cit in Boyer, 1959, p. 198). Newton prova este facto para o
produto
AB da seguinte maneira: seja um rectângulo representado
por AB e sejam os lados A e B diminuídos de 
e 
respectivamente. A área diminuirá então para
.
Sejam
os lados AB aumentados de
e 
respectivamente, a área do triângulo aumentado será então de
Subtraindo do rectângulo maior o rectângulo menor obtém-se aB+bA como o momento do rectângulo original correspondendo aos momentos
a e b de A e
B. Se A=B o momento de 
é
determinado como sendo 2aA. Generalizando para três e mais variáveis, Newton
determina assim que o momento de
é 
em
que a é o momento de A. Este resultado também se aplica no caso
das potências negativas e até no de potências racionais das variáveis.
Newton diz que isto é o fundamento do seu método das tangentes e das
quadraturas; de facto, esta regra combinada com o uso das séries infinitas é
suficiente para chegar a todos os resultados essenciais do método das fluxões.
A base do cálculo tal como ele é publicado nos Principia é para ser encontrado na natureza dos momentos de Newton mas é exactamente aqui que Newton está longe de ser claro. Ele diz sobre esse ponto "Partículas finitas não são momentos mas as quantidades geradas pelos momentos. Devemos considerá-los justamente como os princípios nascentes das magnitudes finitas." (cit in Boyer, 1959, pp. 199,200). Talvez percebendo que esta afirmação torna os seus momentos tão vagos como os infinitesimais de Cavalieri, Fermat e Barrow, ele justifica-se escrevendo "Nem nós neste lema consideramos as magnitudes dos momentos mas as suas proporções primeiras como nascentes." (cit in Boyer, 1959, p. 200). Parece ser isto uma tentativa de introduzir aqui a doutrina dos limites que ele tinha formulado no Livro I, no qual ele considera as razões últimas sem especificar que as quantidades que as compõem o são. De qualquer modo é difícil ver exactamente como é que se pode pensar em limites de razões na determinação do momento de AB pelo que Newton acrescenta outra interpretação "Seria a mesma coisa se em vez dos momentos usássemos as velocidades dos incrementos e dos decrementos ou quaisquer quantidades finitas proporcionais a essas velocidades." (cit in Boyer, 1959, p. 200).
Em suma, as quantidades infinitamente pequenas que Newton usava nos seus trabalhos iniciais levantavam grandes dificuldades conceptuais. Com efeito, estas não eram quantidades finitas nem exactamente nulas. Um crítico no século seguinte, o bispo George Berkeley (1685-1753) chamar-lhes-ia " Fantasmas de quantidades desaparecidas". (cit in Kline, 1990, p. 283). Newton estava bem ciente destas dificuldades, pelo que como vimos em trabalhos posteriores, vai considerar razões de infinitesimais que, em geral, são números finitos. Conhecendo estas razões podia-se agora substituir as quantidades infinitesimais que as formavam por outras magnitudes finitas com a mesma razão. Tais quantidades eram pensadas como sendo as velocidades ou fluxões das quantidades que entravam nas equações. Contudo, não dispondo do conceito rigoroso de limite, o método das fluxões estava dependente dos infinitesimais para a determinação das suas relações básicas. Assim ainda que Newton ligasse o seu método das fluxões com a ideia de uma razão limite, usava tão frequentemente infinitesimais nos cálculos que vamos encontrar mais tarde muitos dos seus sucessores a interpretar as próprias fluxões como quantidades infinitamente pequenas confundindo-os com os momentos. O ponto de vista definitivo de Newton sobre os fundamentos do assunto parece contudo ser aquele que aparece numa sua observação no De quadratura: "procurei demonstrar que no método das fluxões não é necessário introduzir na geometria figuras infinitamente pequenas." (cit in Boyer, 1959, p.202)
