O professor deve conhecer estas formas de aprendizagem. Deve evitar as formas ineficazes e aproveitar as formas eficazes. Deste modo, pode dar bom uso aos três princípios que acabámos de analisar: o princípio da aprendizagem activa, o princípio da melhor motivação, e o princípio das fases consecutivas. Como vimos, estes princípios da aprendizagem são também princípios do ensino. Existe, contudo, uma condição: para tirar proveito de um determinado princípio, o professor não deve apenas conhecê-lo por ouvir dizer. Deve entendê-lo intimamente, com base na sua importante experiência pessoal.

(1) Aprendizagem activa. 

    O que o professor diz na sala de aula não é de forma alguma pouco importante. Mas, o que os alunos pensam é mil vezes mais importante. As ideias deviam nascer na mente dos alunos e o professor devia agir apenas como uma parteira.
    Este é o clássico preceito Socrático e a forma de ensino que a ele melhor se adapta é o diálogo Socrático. O professor do secundário tem definitivamente uma vantagem em relação ao professor universitário na medida em que pode usar o diálogo mais extensivamente. Infelizmente, mesmo no secundário, o tempo é limitado e existem conteúdos pré-estabelecidos para leccionar. Portanto, nem todos os assuntos podem ser discutidos através do diálogo. Contudo, o princípio é este: deixar os alunos descobrir por si próprios tanto quanto for possível.
    Tenho a certeza que é possível fazer muito mais do que normalmente se faz. Deixem-me recomendar-vos um pequeno truque prático: deixem os alunos contribuir activamente para a formulação do problema que eles terão de resolver posteriormente. Se os alunos tiverem participado na formulação do problema, irão depois trabalhá-lo mais activamente.
    De facto, no trabalho de um cientista, a formulação de um problema pode ser a melhor parte da descoberta. Frequentemente, a solução exige menos genialidade e originalidade que a formulação. Assim, permitindo que os alunos participem na formulação, o professor não vai estar apenas a motivá-los para se esforçarem mais mas vai ensinar-lhes uma desejável atitude de pensamento.

(2) Melhor motivação

    O professor deve olhar para si como um comerciante: o seu objectivo é vender alguma matemática aos mais novos. Se o comerciante se depara com resistência por parte dos seus clientes ou mesmo se eles se recusarem a comprar, não deve o comerciante atirar a culpa toda para cima dos clientes. Lembre-se! O cliente tem sempre razão por princípio, e às vezes tem mesmo razão na prática. O rapaz que recusa aprender matemática pode estar correcto. Pode não ser preguiçoso nem estúpido, apenas mais interessado noutra coisa qualquer - há tantas coisas interessantes no mundo á nossa volta. É dever do professor, como comerciante de conhecimentos, convencer o aluno de que a matemática é interessante, que o aspecto em discussão é interessante, que o problema que é suposto resolver merece o seu esforço.
    Portanto, o professor deve prestar atenção na escolha, na formulação e na apresentação adequada do problema que quer propor. O problema deve ter sentido e deve ser relevante do ponto de vista do aluno; deve estar relacionado, se possível, com as experiências diárias dos alunos, e deve ser introduzido através de uma brincadeira ou de um paradoxo. O problema deve ainda partir de conhecimentos muito familiares.Deve conter, se possível, um aspecto de interesse geral ou eventual uso prático. Se desejarmos estimular o aluno a esforçar-se, devemos dar-lhe algum motivo para ele suspeitar que a tarefa merece o seu esforço.
    A melhor motivação é o interesse do aluno na tarefa. Mas existem outras motivações que não devem ser negligenciadas. Deixem-me recomendar um pequeno truque prático: antes dos alunos resolverem um problema, permitam-lhes adivinhar o resultado, ou parte dele. O rapaz que exprimir uma opinião compromete-se; o seu prestígio e auto-estima dependem um pouco do resultado. Vai estar impaciente para saber se o seu palpite está certo ou não e, portanto, vai estar extremamente interessado na sua tarefa e no trabalho da turma. Não irá adormecer ou portar-se mal.
De facto, no trabalho de um cientista, o palpite quase sempre precede a prova. Assim, ao deixar os alunos advinhar o resultado, não vai estar apenas a motivá-los para se esforçarem mais. Vai ensiná-los a ter uma atitude de pensamento desejável.

(3) Fases consecutivas 

    A dificuldade com os problemas nos manuais do secundário é que estes contém quase exclusivamente meros exemplos de rotina. Um exemplo de rotina é um exemplo de curto alcance que ilustra, e permite praticar, as aplicações de apenas uma regra isolada. Tais exemplos de rotina podem ser úteis e até necessários. Não nego. Mas saltam duas importantes fases da aprendizagem: a fase exploratória e a fase de assimilação. Estas duas fases procuram relacionar o problema em causa com o mundo à nossa volta e com outros conhecimentos, a primeira antes e a segunda depois da solução formal. Porém, o problema de rotina está obviamente relacionado com a regra que ilustra e pouco relacionado com quaisquer outras coisas. Por isso há pouco interesse em procurar mais conexões.
    Em contraste com estes problemas de rotina, a escola secundária devia propor problemas mais estimulantes, pelo menos de vez em quando, problemas com contextos ricos que mereçam mais explorações e problemas que possam dar a ideia do trabalho de um cientista.
    Aqui está uma dica prática: se o problema que quer discutir com os seus alunos for adequado, deixe-os fazer uma exploração preliminar: pode abrir o seu apetite para a solução formal. E reserve algum tempo para uma discussão retrospectiva acerca da solução final: pode ajudar na solução de problemas posteriores.

(4) Após esta discussão bastante incompleta, devo terminar a explicação dos três princípios: aprendizagem activa, melhor motivação e fases consecutivas. 

Acho que estes princípios podem infiltrar-se nos pormenores do trabalho diário de um professor e fazer dele um professor melhor. Também acho que estes princípios deviam infiltrar-se na planificação de todo o curriculum, de cada curso do curriculum e de cada capítulo de cada curso.
    Contudo, longe de mim dizer que estes princípios têm que ser aceites. Estes princípios partiram de uma certa visão global, de uma certa filosofia. E o leitor pode ter uma filosofia diferente. Ora, tanto no ensino como em tantas outras coisas, não interessa muito qual é ou não é a sua filosofia. Interessa mais se tem ou não uma filosofia. E interessa muito tentar ou não seguir a sua filosofia. Os únicos princípios do ensino que eu não gosto de forma alguma são aqueles que nos limitamos a papaguear.

6. Exemplos

 

    Os exemplos são melhores que as regras. Deixem-me dar exemplos. Prefiro sem dúvida exemplos a conversas. 

 

    Preocupa-me principalmente o ensino ao nível do secundário e vou apresentar-vos alguns exemplos relativos a esse nível de ensino. Frequentemente sinto grande satisfação nos exemplos a este nível. E posso dizer porquê: tento encará-los de forma a que me recordem a minha experiência matemática. Represento o meu passado a uma escala reduzida.

 

    (1) Um problema do ensino básico -  A forma de arte fundamental do ensino é o diálogo Socrático. Numa turma de ensino básico talvez o professor possa começar assim o diálogo:
"Ao meio-dia em S. Francisco que horas são?"
"Mas, professor, todos nós sabemos isso" pode dizer um jovem activo, ou então "Mas, professor, você é tonto: 12 horas"
"E em Sacramento, ao meio-dia, que horas são?"
"12 horas - claro, não é meia-noite"
"E em Nova Iorque, ao meio-dia, que horas são?"
"12 horas"
"Mas eu pensava que em S. Francisco e Nova Iorque o meio-dia não era à mesma hora, e vocês dizem que é meio-dia em ambos às 12 horas!"

"Bem, é meio-dia em S. Francisco às 12 horas segundo o padrão horário de Oeste e em Nova Iorque às 12 horas segundo o padrão horário de Este."
" E em que padrão horário se encontra Sacramento, Este ou Oeste?"
"Oeste, de certeza"
"As pessoas de S. Francisco e de Sacramento têm o meio-dia no mesmo momento?"
"Não sabem a resposta? Bem, tentem advinhar: será que o meio-dia é mais cedo em S. Francisco, ou em Sacramento, ou será que é no mesmo instante nos dois sítios?"

    O que acham da minha ideia de diálogo Socrático com miúdos do ensino básico? Podem imaginar o resto. Através de questões apropriadas, o professor, imitando Sócrates, deve extrair diversos elementos dos alunos:
a) Temos de distinguir entre meio-dia "astronómico" e meio-dia convencional ou "legal".
b) Definições para os dois meios-dias.
c) Perceber "padrão horário": como e porquê a superfície do globo terrestre está subdividida em zonas de tempo?
d) Formulação do problema: "A que horas do padrão horário do Oeste é o meio-dia astronómico de S. Francisco?"
e) O único dado específico que precisamos para resolver o problema é a longitude de S. Francisco (é uma boa aproximação para o ensino básico).

    O problema não é muito simples. Utilizei-o em duas turmas e, em ambas, os participantes eram professores do secundário. Uma turma demorou cerca de 25 minutos para chegar à solução, a outra demorou 35 minutos.

 

    (2)Devo dizer que este pequeno problema do ensino básico tem várias vantagens -  A principal é o facto de enfatizar uma operação mental essencial que,infelizmente, é negligenciada pelos problemas usuais dos manuais: reconhecer o conceito matemático essencial numa situação concreta. 

    Para resolver este problema, os alunos devem reconhecer a proporcionalidade: as horas numa localidade na superfície do globo terrestre quando o sol está na posição mais vertical variam proporcionalmente com a longitude da localidade.
    De facto, em comparação com os dolorosos e artificiais problemas nos manuais no secundário, o nosso problema é perfeitamente natural, um "verdadeiro" problema. Nos problemas mais difíceis da matemática aplicada, a formulação apropriada do problema é sempre uma parte complicada e, com grande frequência, a parte mais importante. O nosso pequeno problema, que pode ser proposto a uma turma do ensino básico, possui precisamente esta característica. Novamente, os problemas mais difíceis da matemática aplicada podem conduzir a acções práticas, como por exemplo, adoptar um procedimento melhor. O nosso pequeno problema pode explicar aos alunos do ensino básico porque foi adoptado o sistema de 24 zonas horárias, cada uma com um padrão horário uniformizado. No geral, penso que este problema, se for tratado convenientemente pelo professor, pode ajudar um futuro cientista ou engenheiro a descobrir a sua vocação e contribuir para a maturação intelectual daqueles alunos que não vão mais tarde utilizar profissionalmente a matemática.
    Observe-se também que este problema ilustra vários dos pequenos truques mencionados anteriormente: os alunos contribuem activamente na formulação do problema. De facto, a fase exploratória que conduz à formulação do problema é muito importante. Depois, os alunos são convidados a adivinhar um aspecto essencial da solução.

    (3) Um problema do ensino secundário - Vamos considerar outro exemplo. Comecemos por aquele que provavelmente é o problema mais familiar de construções geométricas: construir um triângulo, tendo como dados os três lados. Como a analogia é um campo tão fértil de invenção, é natural perguntar: qual é o problema análogo na geometria a 3 dimensões? Um aluno médio, que tenha alguns conhecimentos de geometria tridimensional, pode ser conduzido a formular o problema: construir um tetraedro, tendo como dados as seis arestas.
    Ora, este problema do tetraedro aproxima-se bastante, no nível secundário comum, dos problemas práticos resolúveis por "desenho mecânico". Engenheiros e designers utilizam desenhos para darem informações precisas acerca dos pormenores de figuras a três dimensões ou estruturas para serem construídas: pretendemos construir um tetraedro com determinadas arestas. Podemos querer, por exemplo, esculpi-lo em madeira.
    Isto leva-nos a perguntar se o problema deve ser resolvido com precisão, usando régua e o compasso, e a discutir a questão: que pormenores do tetraedro devem ser construídos? Eventualmente, após uma discussão na turma bem conduzida, a seguinte formulação definitiva do problema pode emergir:
    Do tetraedro ABCD, são-nos dados os comprimentos das seis arestas AB, BC, CA, AD, BD, CD.Considera o triângulo ABC como a base do tetraedro e constrói com uma régua e um compasso os ângulos que a base forma com as outras três faces.
    O conhecimento destes ângulos é necessário para esculpir em madeira o sólido desejado. Porém, outros elementos do tetraedro podem surgir na discussão. Por exemplo:
a) a altura do vértice D à base,
b) o ponto F sendo este o ponto de projecção do vértice D na base. Note-se que a) e b), que contribuem para o conhecimento do sólido, podem ajudar a encontrar os ângulos pedidos e, por isso, podíamos também tentar construí-los.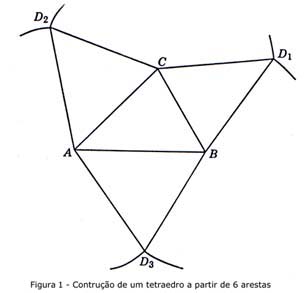

 

    (4) Podemos obviamente, construir as quatro faces triangulares que estão representadas na Fig.1 (pequenas porções de alguns círculos usados na construção foram preservadas para indicar que AD2=AD3, BD3=BD1, CD1=CD2). Se a Fig.1 for copiada para cartão podemos acrescentar-lhe três patilhas, cortar a figura, dobrá-la ao longo de três linhas, e colar as patilhas. Desta maneira obtemos um modelo sólido no qual podemos medir rudemente a altura e os ângulos em questão. Este tipo de trabalho em cartão é bastante sugestivo mas não corresponde ao que nos foi pedido: construir a altura, o seu ponto na base (F), e os ângulos em questão com régua e compasso.

    (5) Pode ajudar pensar no problema ou parte dele "como resolvido". Vamos visualizar o aspecto da Fig.1 quando as três faces laterais forem erguidas para a sua devida posição, após cada uma ter sofrido uma rotação em relação a um lado da base. A Fig.2 mostra a projecção ortogonal do tetraedro no plano da sua base, triângulo ABC. O ponto F é a projecção do vértice D: é a base da altura desenhada a partir de D.

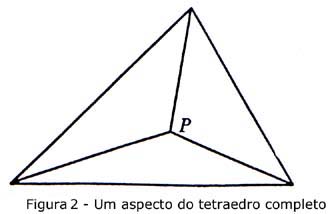
    (6) Podemos visualizar a transição da Fig.1 para a Fig.2 com ou sem o modelo em cartão.    Vamos focar a atenção numa das faces laterais, no triângulo BCD1, que originalmente estava no mesmo plano que o triângulo ABC, no plano da Fig.1 que imaginamos horizontal. Vamos observar o triângulo BCD1 a efectuar uma rotação em torno do lado BC, e fixemos o nosso olhar no único vértice em movimento D1. Este vértice D1 descreve um arco de circunferência. O centro da circunferência é um ponto de BC; o plano deste círculo é perpendicular ao eixo de revolução horizontal BC; além disso, D1 movimenta-se num plano vertical. Portanto, a projecção do percurso do vértice em movimento D1 para o plano horizontal da Fig.1 é uma linha recta, perpendicular a BC, que passa pela posição original de D1.Mas existem mais dois triângulos a efectuar rotações, são três ao todo. Existem três vértices em movimento, cada um seguindo um caminho circular num plano vertical para que destino?

    (7) Penso que o leitor já adivinhou o resultado (talvez até antes de ler o fim da subsecção anterior): as três linhas rectas desenhadas a partir das posições originais (ver Fig.1) de D1, D2, e D3 perpendiculares a BC, CA e AB, respectivamente, intersectam-se num ponto, o ponto F, o nosso objectivo suplementar (b), ver Fig.3. (É suficiente desenhar duas perpendiculares para determinar F, mas podemos usar a terceira para verificar a precisão do nosso desenho). E o que resta fazer é muito fácil. Seja M o ponto de intersecção de D1F com BC (ver Fig.3). Construa o triângulo rectângulo FMD (ver Fig.4), com hipotenusa MD=MD1 e base MF. Obviamente, FD é a altura [o nosso objectivo suplementar a)] e ângulo FMD mede o ângulo diedral formado pela base, o triângulo ABC, e a face lateral, o triângulo DBC que era pedido no nosso problema. 

         

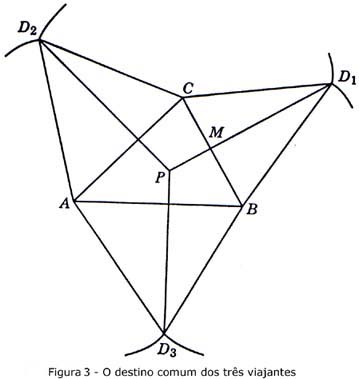
    (8) Uma das virtudes de um bom problema é que gera outros bons problemas.A solução anterior pode, e deve, deixar uma dúvida no seu espírito. Encontrámos o resultado representado pela Fig.3 (que as três perpendiculares descritas acima são concorrentes) tendo em consideração a movimentação de corpos em rotação. No entanto o resultado é uma proposição de geometria e portanto devia ser estabelecida independentemente da noção de movimento, através apenas da geometria. Agora é relativamente fácil libertarmo-nos das considerações anteriores [nas subsecções (6) e (7)] acerca dos conceitos de movimento e estabelecer o resultado através de conceitos de geometria tridimensional (intersecção de esferas, projecção ortogonal). No entanto, o resultado é uma proposição de geometria no plano e portanto devia ser estabelecido independentemente da noção de movimento, através apenas da geometria. (Como?).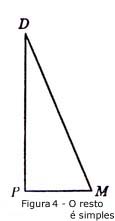

    (9)NOte que este problema do ensino secundário ilustra vários aspectos anteriormente discutidos. Por exemplo, os alunos podiam e deviam participar na formulação final do problema, existe uma fase exploratória e um rico contexto.Contudo há um aspecto que quero enfatizar: o problema está construído para merecer a atenção dos alunos. Embora o problema não esteja muito próximo da realidade diária como o problema do ensino básico, começa por uma parcela de conhecimento bastante familiar (construção de um triângulo através dos três lados), realça desde o início uma ideia de interesse geral (analogia), e aponta para eventuais aplicações práticas (desenho mecânico). Com um pouco de destreza e um pouco de vontade, o professor devia ser capaz de captar a atenção dos alunos, que não estão irremediavelmente aborrecidos, para este problema.

 

7. Aprender ensinando

    Há ainda um tópico para discutir e é um tópico relevante: a formação de professores. Assumo uma posição confortável ao discutir este tema, pois quase posso concordar com a posição oficial (refiro-me às “Recomendações da Associação Americana de Matemática” no que diz respeito à formação de professores, publicada na American Mathematical Monthly, 67 (1960) 982-991. Por questões de brevidade, tomo a liberdade de citar este documento como “recomendações oficiais”). Irei concentrar-me em apenas dois pontos. Pontos aos quais devotei, no passado e praticamente durante os últimos dez anos, grande parte da minha reflexão e do meu trabalho enquanto professor.Fazendo uma aproximação, dos dois pontos que tenho em mente um diz respeito aos cursos “temáticos” e o outro aos cursos sobre “métodos”.

    (1) Cursos Temáticos. É um facto triste mas amplamente visto e reconhecido, que os conhecimentos dos nossos professores de matemática sobre a sua ciência, em escolas secundárias é, em média, insuficiente. Existem, certamente alguns professores bem preparados, mas existem outros (encontrei-me com diversos), cuja boa vontade admiro, mas cuja preparação matemática não é de todo admirável. As “recomendações oficiais” para os cursos temáticos podem não ser perfeitas, mas não há dúvida que a sua aceitação resultaria numa melhoria substancial. Pretendo chamar a vossa atenção para um ponto que, a meu ver, deveria ser acrescentado às “recomendações oficiais”.
    O nosso conhecimento acerca de qualquer assunto consiste em informação e saber1. O saber é a habilidade para usar a informação. Claro que não existe saber sem pensamento independente, originalidade e criatividade. O saber em matemática é a habilidade para fazer problemas, descobrir provas, criticar argumentos, usar linguagem matemática com alguma fluência, reconhecer os conceitos matemáticos em situações concretas.
Todos concordamos que, em matemática, o saber é mais importante, ou melhor, é muito mais importante do que possuir informação. Todos exigem que o ensino secundário deve fornecer os estudantes, não apenas informação em matemática, mas com saber, independência, originalidade e criatividade. E, no entanto, quase ninguém pede que o professor de matemática possua estas coisas bonitas – não é espantoso? 
    As “recomendações oficiais” são silenciosas no que diz respeito ao saber matemático dos professores. 
O estudante de matemática que trabalha para um doutoramento, deve fazer pesquisa mas, antes disso, deve ter encontrado oportunidade para realizar trabalho independente em seminários sobre problemas, ou na preparação da sua tese de mestrado. No entanto, este tipo de oportunidade não é oferecida ao futuro professor de matemática. Nas “recomendações oficiais” não existe qualquer palavra acerca de uma qualquer espécie de trabalho independente ou pesquisa. Se, entretanto, o professor não tiver tido qualquer experiência em trabalhos criativos de algum tipo, como é que vai ser capaz de inspirar, de orientar, de ajudar ou mesmo de reconhecer a actividade criativa dos seus estudantes? Um professor que adquiriu o que quer que seja que sabe em matemática apenas de forma receptiva dificilmente pode promover o estudo activo dos seus estudantes. Um professor que nunca teve, em toda a sua vida, uma ideia brilhante, vai provavelmente repreender, em vez de ajudar, um estudante que a tenha.
    Na minha opinião, a pior falta no conhecimento matemático da média dos professores do ensino secundário é o facto de não terem experiência em trabalhos activos de matemática e, desta forma, não terem real mestria, mesmo no que diz respeito ao currículo da escola secundária que é suposto ensinarem.
    Não tenho nenhum remédio milagroso para oferecer mas vou tentar uma coisa. Tenho vindo a introduzir e a conduzir repetidamente um seminário sobre resolução de problemas para professores. Os problemas apresentados neste seminário não requerem muito conhecimento para além do nível do ensino secundário, mas requerem algum grau, e por vezes um alto grau, de concentração e juízo independente – e a solução para esses problemas requere trabalho “criativo”. Tenho tentado organizar o meu seminário para que os estudantes sejam capazes de utilizar muito do material proposto para as suas aulas sem grandes alterações, para que possam adquirir alguma mestria no ensino da matemática no secundário e também para que possam ter algumas oportunidades de praticar o ensino (ensinando-se uns aos outros, em pequenos grupos).

    (2) Cursos sobre Métodos. Do meu contacto com centenas de professores de matemática retirei a impressão de que os cursos sobre “métodos” são frequentemente recebidos com verdadeiro entusiasmo. Os cursos mais usuais oferecidos pelos departamentos de matemática são da mesma maneira recebidos pelos professores. Um professor com quem tive uma conversa aberta sobre estas matérias encontrou uma expressão pitoresca para um sentimento muito disseminado: “ O departamento de matemática oferece-nos um bife duro que não conseguimos mastigar e a escola da educação uma sopa ligeira sem nenhuma carne”.
    De facto, devemos por uma vez assumir alguma coragem e discutir publicamente a questão: Os cursos sobre métodos são de facto úteis de alguma maneira? Há mais hipóteses de chegar à resposta certa numa discussão aberta do que numa aceitação generalizada.
    A questão envolve questões pertinentes em número suficiente. Será que ensinar é ensinável? (Ensinar é uma arte, como muitos de nós pensamos – e uma arte é ensinável?) Existe alguma coisa que se possa denominar de métodos de ensino? (O que o professor ensina, nunca é melhor do que o professor é; ensinar depende da personalidade do professor – existem tantos métodos bons como existem professores bons). O tempo permitiu que a formação de professores se tenha dividido entre cursos temáticos, cursos sobre métodos e prática de ensino. Devemos despender menos tempo nos cursos sobre métodos? (muitos países europeus gastam muito menos tempo). 
    Espero que as pessoas mais novas e mais vigorosas que eu próprio levantem estas questões algum dia e as discutam com uma mente aberta e informações relevantes.
    Falo-vos aqui apenas e acerca da minha experiência e apenas das minhas opiniões. De facto, já respondi de forma implícita à questão primordial. Acredito que os cursos sobre métodos podem ser vantajosos. Na verdade, o que apresentei foi uma amostra de cursos sobre métodos, ou melhor, um resumo de alguns tópicos, os quais, na minha opinião, devem ser oferecidos cursos sobre métodos aos professores de matemática. 
    Todas as classes que leccionei a professores de matemática deveriam, na sua maioria, ser entendidas como cursos sobre métodos. A designação dessas classes mencionava alguns temas e o tempo era realmente dividido em temas e métodos: talvez nove décimos para os temas e um décimo para os métodos. Sempre que possível, a classe era dirigida sob forma dialógica.

     Incidentalmente, eram apresentados por mim ou pela audiência, algumas observações metodológicas. Na verdade, a derivação de um facto ou a solução de um problema era quase regularmente seguida de uma curta discussão das suas implicações pedagógicas. “ Poderá isto ser utilizado na vossa turma?”, perguntava eu à audiência “ Em que estádio do currículo imaginam utilizá-las? Quais os pontos que precisam de especial cuidado? Como poderiam tentar ultrapassa-los?” E questões desta natureza (especificadas, de forma apropriada) foram também regularmente propostas nos exames.
No entanto, o meu trabalho principal era escolher os problemas (como os dois que aqui apresentei) capazes de ilustrar de forma clara algum padrão do ensino. 

    (3) As “recomendações oficiais” chamadas cursos sobre “métodos” e cursos sobre o “estudo do currículo” não são muito eloquentes acerca desses padrões. Na minha opinião, é possível contudo encontrar uma excelente recomendação. Algo escondido, para cuja descoberta tem que somar dois mais dois combinando a última premissa em “cursos de estudo de currículo” com recomendações para o nível IV. Mas é claramente suficiente: um professor universitário que lecciona um curso sobre métodos para professores de matemática deveria saber matemática pelo menos ao nível de um mestrado. Gostaria de acrescentar: deveria também ter alguma experiência, mesmo que modesta, de investigação em matemática. Se não tiver tal experiência como poderá convir que o mais importante para um futuro professor é, o espírito de trabalho criativo?
Até agora ouviram suficientes recordações de um velho homem. Algo concreto e bom pode sair daqui se dedicarmos alguma reflexão à seguinte proposta resulta até da discussão antecedente. Proponho que os seguintes dois pontos sejam acrescentados às “recomendações oficiais” da Associação:

I. A formação de professores de matemática deve oferecer experiência em trabalho independente (“criativo”) a um nível apropriado sob a forma de Seminário sobre a resolução de problemas ou de outra forma adequada.

II. Os curso sobre métodos devem ser oferecidos aos professores apenas uma ligação estreita com os cursos temáticos ou com prática de ensinar e se praticável, apenas por professores experientes, tanto em pesquisa matemática como em ensino.

8. A atitude dos professores

    Como referi anteriormente, as minhas classes destinadas a professores foram na, sua maioria, cursos sobre métodos. Nessas classes procurei atingir pontos de utilização prática imediata a serem usados diariamente nas tarefas dos professores. Por esta razão, inevitavelmente, tive que expressar a minha perspectiva sobre o dia-a-dia das tarefas dos professores e sobre as suas atitudes. Os meus comentários tenderam a assumir um carácter organizado razão pela qual os condensei em “Dez mandamentos para Professores”. Quero agora acrescentar alguns comentários sobre essas dez regras.
    Na formulação dessas regras, tive em conta os participantes das minhas aulas, professores que ensinam matemática no ensino secundário. Contudo, estas regras são aplicáveis a qualquer situação de ensino, a qualquer assunto e a todos os níveis, mas especificamente ao nível do ensino secundário.
    No entanto, os professores de matemática têm mais e melhores oportunidades de aplicar algumas delas do que os professores de outras cadeiras, e isto refere-se em particular às regras 6, 7 e 8.

 

DEZ MANDAMENTOS PARA PROFESSORES   1. Seja interessado na sua ciência. 2. Conheça a sua ciência. 3. Conheça as formas de aprendizagem. A melhor maneira de aprender algo é descobri-lo por si mesmo. 4. Tente ler nas faces dos seus estudantes, tente ver as suas expectativas e dificuldades, ponha-se no lugar deles. 5. Dê-lhes não só a informação mas também saber, formas de raciocínio, hábitos de trabalho com método. 6. Permita que aprendam por descoberta. 7. Permita que aprendam provando. 8. Encare as características do problema em mãos como podendo ser úteis na resolução de outros problemas – Tente descobrir o padrão geral que está por detrás da situação concreta presente. 9. Não partilhe o seu segredo todo de uma vez só – Permita que os alunos o adivinhem antes que o diga – deixe que descubram por si mesmos, tanto quanto for possível. 10. Sugira as coisas, não force os alunos a aceitar.

 

A tradução dos tópicos de 1 a 6 foi realizada por Elisa Mosquito, Ricardo Incácio e Teresa Ferreira que elaboraram 3 breves comentários. Os pontos 7 e 8 foram traduzidos por Sara Cravo. Revisão de Olga Pombo

VOLTAR