Sabemos que a matemática egípcia se baseava no sistema decimal aditivo e não posicional, como é o nosso. As operações básicas de soma e subtracção limitavam-se a uma combinação ou cancelamento de símbolos. A adição era a base das operações de subtracção, multiplicação e divisão.
![]() Para somar
juntavam-se, simplesmente, os símbolos correspondentes. Como os símbolos se podiam repetir desde
1 a 9 vezes, se se excediam as 9 vezes eliminavam-se 10 e acrescentava-se o símbolo
correspondente à potência de 10 seguinte. Por exemplo:
Para somar
juntavam-se, simplesmente, os símbolos correspondentes. Como os símbolos se podiam repetir desde
1 a 9 vezes, se se excediam as 9 vezes eliminavam-se 10 e acrescentava-se o símbolo
correspondente à potência de 10 seguinte. Por exemplo:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() +
+ ![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ao obtermos 11 símbolos
![]() eliminavam-se 10 e acrescentava-se o equivalente (
eliminavam-se 10 e acrescentava-se o equivalente (![]() )
obtendo-se,
)
obtendo-se,
![]()
![]()
![]()
![]()
![]()
O sistema é trivial, assemelhando-se ao funcionamento de um ábaco.
![]() Para a subtracção
eliminavam-se, simplesmente, os símbolos que se anulavam. Por exemplo:
Para a subtracção
eliminavam-se, simplesmente, os símbolos que se anulavam. Por exemplo:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -
- ![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]() Para multiplicar aplica-se um sistema de duplicação - adição. Este sistema
baseia-se na propriedade de qualquer número natural se poder expressar como uma
soma de potências de 2.
Para multiplicar aplica-se um sistema de duplicação - adição. Este sistema
baseia-se na propriedade de qualquer número natural se poder expressar como uma
soma de potências de 2.
Se quiséssemos multiplicar, por exemplo, n X m far-se-ia do seguinte modo:
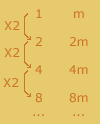 |
A tabela continua até que o valor seguinte seja menor que n. Depois trata-se de decompor o número n como soma dos valores da 1º coluna e o total será dado pela soma dos valores correspondentes da 2ª coluna. |
Vejamos o exemplo de 6 X 3 :
| 1 | 3 | |
|
* |
2 | 6 |
| * | 4 | 12 |
| 6=4+2 | 18=6+12 |
Como 4 X 2 = 8 > 6, não se efectuam mais multiplicações. Logo 6 X 3 = 18.
![]() Para a divisão o
método era bastante curioso: baseia-se na multiplicação e obtém-se sempre quantidades inteiras ou fracções exactas.
Para a divisão o
método era bastante curioso: baseia-se na multiplicação e obtém-se sempre quantidades inteiras ou fracções exactas.
Se se queria dividir n / m então o método consistia em obter o número m e o número de partes de m que somam o número n.
 |
A tabela continua até que o valor da 2ª coluna se tornasse maior que n. Depois bastava escrever n como soma dos valores dessa coluna e o resultado da divisão n/m seria a soma dos valores correspondentes da primeira coluna. |
Vejamos o exemplo 21/3 :
| * | 1 | 3 |
|
* |
2 | 6 |
| * | 4 | 12 |
| 7=1+2+4 | 21=3+6+12 |
Como 12 X 2 = 24 > 21 então não se efectuam mais multiplicações. Logo 21:3 = 7.