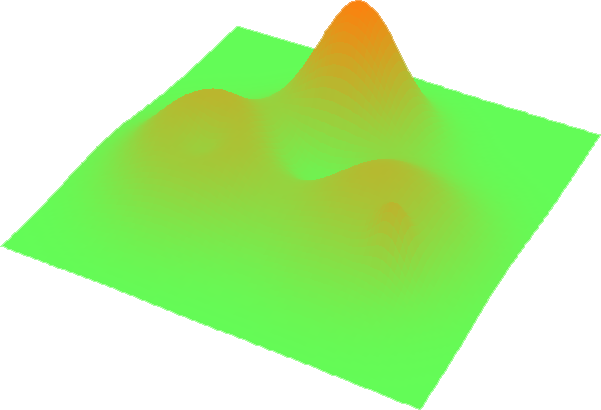
A figura acima é o gráfico de uma função $f$ representando um relevo topográfico e $\,f^{-1}(c)$ corresponde ao nível do mar. Clique na carta seguinte spara fazer subir o nível da água.
|
Teorema de Morse
Seja $f\colon X\to\mathbb{R}$ uma função diferenciável tal que $X = \{ f\geq c\}$ e $\partial X = f^{-1}(c)$ é um nível regular de $f$.
Então
$$ C_i(f) \geq \beta_i(X,\mathbb{K})$$ $$ \chi(X) = \sum_{i=0}^{\dim X} (-1)^i \, C_i(f) . $$ onde $C_i(f) =$ número de pontos críticos de $f$ com índice $i$.
Se $X$ é uma superfície
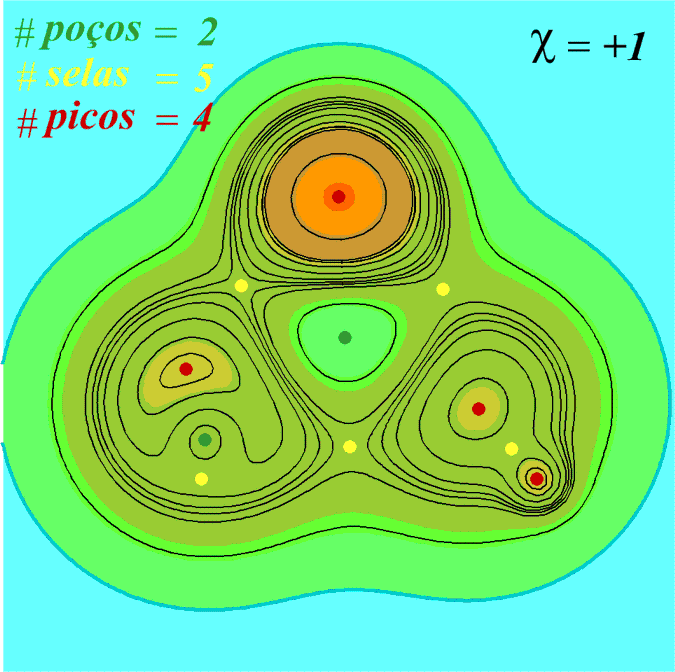
( $\#$ picos de $f$ ) - ( $\#$ selas de $f$ ) + ( $\#$ poços de $f$ ) = $\chi(X)$ ,onde $\beta_i(X,\mathbb{K}) =$ $i$-ésimo número de Betti de $X$.
( $\#$ picos de $f$ ) $\geq \beta_0(X,\mathbb{K})$
( $\#$ selas de $f$ ) $\geq \beta_1(X,\mathbb{K})$
( $\#$ poços de $f$ ) $\geq \beta_2(X,\mathbb{K})$

A figura acima é o gráfico de uma função $f$ representando um relevo topográfico e $\,f^{-1}(c)$ corresponde ao nível do mar. Clique na carta seguinte spara fazer subir o nível da água.

|
>> Teoria de Morse