|
|
| Teoria
epidemiológica
A epidemiologia
das doenças transmissíveis dos humanos, resulta da
interacção entre 3 factores: (1) A interacção
entre o hospedeiro humano e o agente da doença, a nível
individual, (2) O processo de transmissão entre hospedeiros
e a forma como este é influenciado por aspectos sócio-culturais
do hospedeiro e (3) As características demográficas
da população humana. O impacto da vacinação
sobre a epidemiologia da doença, é determinado pelas
características da vacinação e por estes factores.
A tomada
em consideração dos 3 factores, em simultâneo,
é feita recorrendo a instrumentos matemáticos. Raciocínios
meramente intuitivos são em geral insuficientes para lidar
com a dinâmica de sistemas com este grau de complexidade. |

Dificuldade com termos
aqui usados ?
tente o dicionário.
Sugestões de termos a
adicionar ao dicionário ?
contacte-me
|
| Dois
tipos de abordagem epidemiológica
1. Epidemiologia descritiva
A epidemiologia de doenças transmissíveis
(DTs), pode ser abordada de duas formas complementares. Uma, clássica,
consiste no recurso a instrumentos da estatística para descrever
a incidência e/ou a prevalência da doença, no
tempo e no espaço. Um exemplo simples, é o cálculo
do número médio de casos de doença por unidade
de tempo ou o cálculo da taxa de letalidade. Outros exemplos,
mais complexos, são a utilização de técnicas
de séries temporais, o ajuste do modelo linear (regressão,
ANOVA etc) ou as análises multivariadas (componentes principais,
cluster analysis ...) para descrever fenómenos epidemiológicos.
Mas por muito bem que estas abordagens descrevam ou revelem os padrões
epidemiológicos duma DT, elas não explicam
as razões da epidemiologia observada. São meramente
descritivas. Há quem lhes chame fenomenológicas, pois
apenas descrevem fenómenos. Existem estudos destes em Portugal
(ver 17 e,
especialmente o 20
). Outra forma de abordar a epidemiologia
de DTs consiste em recorrer a modelos matemáticos explicativos
ou analíticos.
2. Epidemiologia analítica
Na abordagem analítica,
o epidemiologista expõe explícitamente os seus pressupostos
acerca dos 3 factores determinantes da epidemiologia (ver caixa
azul acima) e estuda matemáticamente as consequências
desses pressupostos através de modelos cuja construção
e análise, em geral, requerem alguma formação
matemática. Idealmente, os pressupostos conduzem a previsões
da epidemiologia da doença que não diferem muito dos
dados reais. Se tal não acontecer, os pressupostos devem
ser revistos.
Seguidamente revejo o papel da teoria
matemática em epidemiologia de DTs e apresento alguns resultados
relevantes para a vacinação. Uma introdução
mais completa ao assunto é apresentada na disciplina de Dinâmica
de Doenças Infecciosas que lecciono. Os tópicos
a abordar aqui são os seguintes:
Porquê
matemática ?
Modelos matemáticos de doenças
transmissíveis
Dinâmica de doenças transmissiveis
e R0
Epidemias
Controle de doenças transmissiveis
por vacinação
Eliminação de doenças
transmissíveis por vacinação
E quando a vacinação não
elimina a doença ?
|
| |
Porquê matemática
? A epidemiologia estuda a
incidência das DTs em grandes populações. Ao
longo dos anos, os epidemiologistas recorreram à estatística
para descrever os seus dados e formular as suas hipóteses.
A epidemiologia clássica está muito associada à
descrição do número de casos de doença
por milhares de habitantes, por área geográfica e/ou
unidade de tempo. Esta descrição pode-se resumir a
simples gráficos de barras, técnicas de mapeamento
ou mesmo a sofisticados métodos de análise multivariada.
Mas nas últimas décadas houve tambem avanços
significativos na compreensão da propagação
das doenças transmissíveis em grandes populações,
os quais resultaram do recurso a modelos matemáticos menos
familiares. As conclusões destes estudos são tão
importantes que hoje desempenham um papel importante na concepção
dos programas de controle de DTs nos países desenvolvidos.
Mas porquê o recursos a modelos matemáticos ?
A infecção, patologia
e sintomatologia da maioria das doenças infecciosas humanas
são razoávelmente compreendidas. Este conhecimento,
porém, não é suficiente para prever a forma
como a doença se vai propagar numa grande população.
Para isso, há que ter em consideração factores
que complicam imensamente a investigação. Estes factores
são a biologia do agente infeccioso (ciclo de vida, vulnerabilidade
a factores climáticos), as características demográficas
da população infectada (natalidade, mortalidade de
infectados e não-infectados, estrutura etária, distribuição
no espaço), aspectos comportamentais (taxas de contacto entre
indivíduos, higiene, etc.) e, evidentemente, eventuais medidas
de controle (vacinação, isolamento de infectados,
etc). A complexidade do assunto impossibilita portanto que se possa
prever o curso de uma epidemia, por exemplo, baseando-nos apenas
na intuição. Pelo contrário, é necessário
integrar toda a informação relevante de forma eficaz
e esta integração pode ser feita verbalmente, gráficamente
ou, de preferência, através de modelos matemáticos.
A matemática oferece os instrumentos mais adequados à
expressão de relações complexas de uma forma
que torna relativamente fácil avaliar as consequências
dessas relações. Trata-se de uma ciência que
obriga o investigador a (fazer um esforço para) expôr
com máxima exactidão as suas ideias sobre os factores
que determinam a epidemiologia da doença e permite investigar
as consequências dessas ideias. Não seria impossível
expôr verbalmente as informações contidas nas
equações dos modelos matemáticos, mas a matemática
oferece uma forma mais poderosa de sumarizar estas informações
e, pela disciplina mental que impõe, impede que se deslize
para raciocínios confusos.
|
|
| |
Modelos matemáticos de
doenças transmissíveis Os
modelos mais frequentemente usados para descrever a dinâmica
de DTs são do tipo compartimental. A população
hospedeira é dividida em categorias ou “compartimentos”.
Estas categorias têm em atenção o percurso por
que passa um hospedeiro infectado e a forma como a infecção
se transmite. Considere-se, por exemplo, uma doença como
o sarampo. Numa população em que o sarampo é
endémico, práticamente todos os recém-nascidos
nascem com imunidade passiva herdada da mãe. Passados alguns
meses, estas crianças tornam-se susceptíveis e, mais
tarde ou mais cedo, entram em contacto com o vírus. Entre
o momento de recepção do vírus e o momento
em que o infectado se torna capaz de o transmitir, decorre um periodo
de alguns dias, designado por periodo de latência, durante
o qual se inicia a virémia. Logo que o infectado se torna
capaz de transmitir a doença, termina o periodo de latência
e inicia-se o periodo de infecciosidade. Eventualmente, o infectado
recupera da doença e, em principio, torna-se imune para toda
a vida. Este percurso da infecção a nivel individual,
permite conceptualizar a população dividida em cinco
categorias de indivíduos. Na primeira temos os bebés
com protecção maternal (P) ao sarampo,
na segunda os susceptíveis (S), depois
a categoria dos indivíduos que estão em periodo de
latência (E), a categoria dos infecciosos
(I) e, finalmente, a categoria que inclui todos os indivíduos
imunes ou removidos (R) do processo de transmissão.
Numa população muito grande, existe um fluxo permanente
de indivíduos entre estas cinco categorias e, se se assumir
que a imunidade ao sarampo, uma vez adquirida, permanece toda a
vida, o fluxo decorre sempre no sentido que acaba de ser descrito:
dos protegidos até aos recuperados:
|

página de abertura

dicionário |
| |
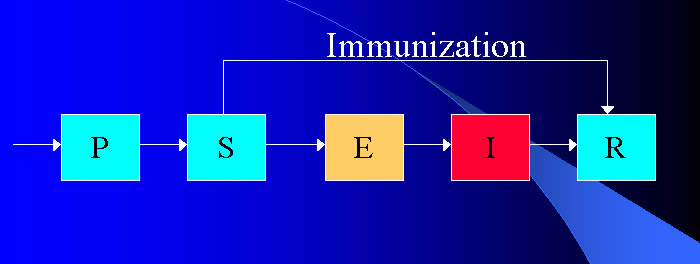
Fluxo de indivíduos
num modelo compartimental gráfico simples do sarampo. Notar
o fluxo devido à imunização por meio de vacinação
em massa de indivíduos susceptíveis que são
deslocados para o compartimento dos removidos. |
| |
Numa população muito grande,
a transferência de indivíduos entre compartimentos é
um fenómeno contínuo. É por isso possivel representar
matemáticamente a variação do número de
indivíduos dentro de cada compartimento, à medida que
o tempo passa, por sistemas de equações diferenciais.
Estes sistemas de equações podem ter solução
analítica mas, quando o modelo tem um mínimo de realismo,
isso raramente acontece e torna-se necessário implementar computacionalmente
o sistema de equações. Há várias perguntas
às quais o sistema de equações pode dar resposta.
Por exemplo, como é que varia o número de indivíduos
no compartimento dos infecciosos à medida que o tempo passa
? devem-se esperar epidemias periódicas ou, pelo contrário,
a doença tende a permanecer endémica na população
com um determinado nivel de morbilidade ? Quais são as consequências
da introdução de um programa de controle por vacinação
? Em que condições é que este programa conseguirá
eliminar a infecção ? O
exemplo dado para o sarampo é relativamente simples, mas
serve para ilustrar a abordagem geralmente adoptada. A informação
sobre o percurso individual da infecção, pormenores
do processo de transmissão de indivíduo para indivíduo
e todas as informações relevantes disponíveis,
são integradas, primeiro gráficamente e depois matemáticamente.
A complexidade do modelo depende do grau de realismo que se atinge
e da complexidade da própria doença. Na tuberculose,
por exemplo, existem mais compartimentos do que no sarampo, pois
há mais estádios pelos quais os infectados podem passar.
Nas doenças sexualmente transmitidas, um outro exemplo, são
necessários compartimentos separados para os dois sexos.
Nas doenças associadas a grupos sociais de risco, há
que dar um tratamento separado a estes grupos, usando compartimentos
com características diferentes e tendo em atenção
que a probabilidade de contágio varia de grupo para grupo.
Dinâmica
de doenças transmissiveis e R0
O número de pessoas infectadas
por uma DT num dado instante (a prevalência da doença),
bem como o número de novos infectados por unidade de tempo
(a incidência da doença), variam à medida que
o tempo passa. O estudo desta variação é designado
por estudo da dinâmica da doença e pode ser feito recorrendo
a modelos matemáticos como os que foram referidos acima.
Quando não existe qualquer controle da infecção
(por vacinação, isolamento de infectados, etc.), cada
doença adquire uma dinâmica própria. Por exemplo,
algumas doenças tornam-se endémicas, com uma prevalência
média que não varia muito de ano para ano, apresentando
quanto muito uma variação sazonal típica. Outras
geram uma epidemia e depois desaparecem, a menos que haja re-introduções
de infecciosos vindos de fora. Outras doenças tornam-se endémicas
e originam epidemias mais ou menos regulares, com uma periodicidade
que pode ser determinada.
Os modelos matemáticos têm
sido muitas vezes capazes de recriar estas dinâmicas em computador,
ajudando-nos a compreender a causa das mesmas e, ao mesmo tempo,
dando-nos alguma capacidade de predicção acerca daquilo
que podemos esperar de uma DT numa população com determinadas
cararacterísticas demográficas e sócio-culturais.
Foi possível, por exemplo, demonstrar o papel crucial que
desempenha o número básico de reprodução
da doença, simbólicamente representado por R0.
O número básico de reprodução é
o número médio de novos infectados gerados por um
indivíduo infeccioso quando este é introduzido numa
população em que todos os indivíduos são
susceptíveis à infecção. R0
é portanto o número de contactos "adequados"
tidos por um infeccioso. R0 é em geral
superior a 1 (a maioria das doenças tem um valor de R0
entre 7 e 20), e isso é condição necessária
para que a doença se possa propagar. Mas não é
condição suficiente. Numa população
real, nem todos os indivíduos contactados são susceptíveis
- alguns são imunes - e, por isso, parte dos R0
contactos não conduzem a novas infecções.
Se houver muitos imunes, cada indivíduo infeccioso pode infectar
menos do que um susceptível, deixando menos do que um “substituto”
antes de se curar (ou deixar de ser infeccioso) e, assim, a doença
acaba por ser eliminada da população. Esta é
a lógica subjacente à vacinação em massa.
Um dos objectivos consiste em baixar a percentagem de susceptíveis
na população a um nivel tão baixo que o número
médio de “substitutos” de cada infeccioso seja
inferior a 1.
A quantidade R0,
crucial para compreender a dinâmica da doença, é
extremamente difícil de medir directamente na população.
Uma das grandes conquistas da epidemiologia moderna foi conseguir
estabelecer relações matemáticas entre R0
e outros parâmetros epidemiológicos mais fáceis
de medir. É possivel demonstrar que, sob certas condições
demográficas, existe uma relação simples entre
R0, a longevidade média da população
(L) e a idade média em que a doença é contraída
pela primeira vez (A) quando não há medidas de controle
da doença: R0=L/A.
Por exemplo, numa população com longevidade média
de L=75 anos, onde se constatou que uma doença endémica
é, em média, contraída aos A=8 anos de idade,
o valor esperado de R0 para esta doença
é de aproximadamente 9.4 contactos (=75/8).
|
|
| |
Epidemias Os
modelos matemáticos têm ajudado a compreender a razão
por que certas doenças endémicas originam regularmente
epidemias e fornecem até instrumentos para calcular a periodicidade
destas epidemias. Uma epidemia só ocorre quando o número
de “substitutos”, acima referido, é superior
a 1. Por outras palavras, quando cada infeccioso deixa a “substitui-lo”
mais do que um infectado antes de se curar. No decorrer da epidemia,
há um número enorme de susceptíveis que é
“consumido” pela infecção. Em doenças
como o sarampo ou a papeira, a recuperação da doença
confere, só por si, imunidade à mesma, pelo que a
certa altura os susceptíveis à infecção
começam a escassear. Um infeccioso começa então
a ter dificuldade em encontrar susceptíveis para o “substituirem”.
Note-se que o valor médio de R0, em
principio, não se terá alterado: os susceptíveis
é que começam a escassear. De facto, embora os susceptíveis
continuem a ser fornecidos à população através
dos nascimentos, a velocidade de propagação da epidemia
(medida pela incidência) é em geral tão rápida
que supera largamente a taxa de natalidade. Quando o número
de “substitutos” se torna menor que 1, a epidemia regride
e a doença volta para niveis de endemismo muito baixos. Não
é eliminada, mas passa despercebida num pequeno número
de infectados. Com o passar do tempo, os nascimentos vão
trazendo à população novos susceptíveis
à doença. O “balão” de susceptíveis
aumenta lentamente, ao ritmo da taxa de natalidade, recomeçando
a criar terreno para nova epidemia. A certa altura, a concentração
de susceptíveis, que já é relativamente elevada
na população total, torna-se particularmente elevada
numa dada área geográfica onde há infectados
(por exemplo num bairro urbano). Se houver condições
apropriadas, o número de substitutos torna-se então
súbitamente muito elevado e dispara uma nova vaga epidémica.
A existência destas oscilações
na incidência da doença, vulgarmente conhecidas por
epidemias, são matemáticamente demonstráveis
e podem ser reproduzidas computacionalmente. A teoria matemática
fornece mesmo instrumentos para prever a sua periodicidade. Se se
designar por T o período de tempo que decorre entre duas
epidemias (o chamado período inter-epidémico), por
G o período de latência (ver Modelos
matemáticos de doenças transmissíveis),
por C o periodo de infecciosidade característico da doença
em causa e, finalmente, por A a idade média em que a doença
é contraída na população, demonstra-se
que:
Pode-se portanto esperar que as epidemias
ocorram mais frequentemente (T menor) quando A é mais baixo,
o que por sua vez implica R0 elevado (recordar
R0=L/A) ou quando o periodo de infecciosidade
é mais curto.
A teoria matemática prevê
também que só as doenças que se enquadram na
dinâmica acima descrita de “enchimento-esvaziamento”
do “balão” de susceptíveis é que
devem originar epidemias regulares e periódicas, com T previsto
pela equação acima. É o caso do sarampo, rubéola,
papeira, etc. Doenças endémicas em que o “consumo”
de susceptíveis decorre de forma mais lenta e/ou contínua,
como é o caso de doenças com R0
baixo, doenças com portadores crónicos, ou doenças
em que a recuperação da doença não confere
imunidade à mesma (p. ex. muitas infecções
bacterianas) não devem gerar oscilações periódicas
regulares. A análise estatística da incidência
da tuberculose, difteria, tétano, hepatite B, gonorreia etc.,
ao longo dos anos, parece confirmar esta previsão, uma vez
que estas doenças não exibem epidemias periódicas
regulares.
|


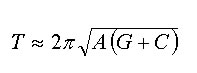
|
| |
Controle de doenças transmissíveis
por vacinação
O
gráfico do modelo compartimental do sarampo apresentado acima
(Modelos matemáticos de doenças
transmissíveis) indica que é possivel incorporar
nos modelos medidas de controle como a vacinação. De
facto, vacinar indivíduos regularmente, equivale a estabelecer
um fluxo permanente de indivíduos de uma categoria populacional
(os susceptíveis) para outra (os imunes). Este fluxo pode ser
representado matemáticamente e é possivel estudar as
consequências que um programa de vacinação deve
ter sobre a incidência de uma DT. Exemplos de perguntas relevantes
a que os modelos matemáticos têm tentado responder são:
Qual é a percentagem de cobertura vacinal necessária
para eliminar uma doença infecciosa num país ?
Qual é a importância que tem a idade em que se vacina
os indivíduos ?
Quando a vacinação não elimina a doença,
que impacto se pode esperar que a vacinação tenha sobre
as epidemias da doença ?
Vale sempre a pena efectuar vacinação em massa ?
Vejamos resumidamente alguns resultados,
bem estabelecidos, que dizem respeito ao tipo de vacinação
praticado em Portugal.
|
|
| |
Eliminação de doenças
por vacinação Considere-se
um programa de vacinação caracterizado por imunizar
todos os anos uma certa percentagem de crianças quando estas
atingem V anos de idade. Chamemos pc à
proporção mínima destas crianças que
tem de ser imunizada todos os anos para se conseguir eliminar a
doença. Demonstra-se que:
pc
= 1 - (1/R0)
(para R0 ver
Dinâmica de doenças transmissiveis
e R0). Para se ter uma ideia da dificuldade
que este esforço de imunização representa,
considere-se o caso do sarampo em Portugal. Antes da vacinação,
a doença era, em média, contraída por volta
de A = 6 anos de idade. Assumindo que a longevidade da população
portuguesa rondava então os L= 70 anos de idade e, usando
a expressão já acima apresentada, R0
= L/A, tira-se que R0 = 70/6 = 11.7 para o
sarampo em Portugal. Então, pc = 1
- 1/11.7 = 0.91. Quer dizer,
com uma dose de vacina anti-sarampo, é necessário
imunizar 91% de todas as crianças que atingem a idade V todos
os anos. Como a eficácia da vacina anti-sarampo ronda os
95%, isto significa que é necessário vacinar (0.91/0.95)x100%,
isto é, 96% de crianças todos os anos. Um objectivo
muito ambicioso para o PNV de qualquer país do mundo. Para
outras doenças infecciosas que não o sarampo, recorde-se
que R0 se situa habitualmente entre 7 e 20,
para se poder avaliar o elevado valor de pc
que a eliminação requer.
Como é que pc
é influenciado pela idade V em que a vacina é dada?
Demonstra-se que existe a seguinte relação entre pc,
a longevidade (L) da população, a idade média
de contracção da doença antes da vacinação
(A) e V:
pc = (L-A) /
(L-V)
Quanto maior fôr V, menor é o valor do denominador
e maior fica o valor de pc. Por outras palavras,
quanto mais tarde se vacinar pior. No caso extremo em que V >
A, o numerador fica maior do que o denominador e então, pc
> 1. Por outras palavras, seria necessário imunizar mais
de 100% das crianças na idade V para eliminar a doença
- a eliminação é completamente impossivel nessas
circunstâncias.
Vacinar com mais do que uma dose, como
se recomenda hoje em dia em Portugal para a VASPR, aos 15 meses
e aos 6 anos de idade (ver PNV),
aumenta as chances de eliminação destas doenças
? Os resultados da investigação deste assunto são
menos simples do que os anteriores, pelo que se optou por ilustrar
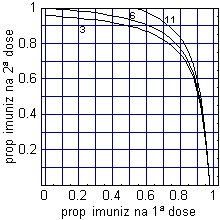
os mesmos gráficamente. No gráfico ao lado, as abcissas
representam a proporção de crianças que são
imunizadas na idade em que é dada a primeira dose da vacina
(aos 15 meses de idade), chamemos-lhe q1. As ordenadas representam
a proporção de crianças ainda susceptíveis
quando atingem a idade da segunda dose e que são, por sua
vez, imunizadas com a segunda dose da vacina. Chamemos a essa proporção
q2 . As curvas a cheio no gráfico unem todos os pares ordenados
(q1, q2) capazes de eliminar a doença para três situações:
quando a segunda dose é dada aos 3, 6 ou 11 anos de idade.
A forma desta curva é típica para várias doenças
infantis, nomeadamente para o sarampo, papeira e rubéola,
as doenças que a VASPR combate.
Há algumas conclusões
interessantes que se podem tirar deste gráfico. A primeira
conclusão é que, para conseguir a eliminação
destas doenças, é crucial a manutenção
de uma elevada percentagem de cobertura vacinal na primeira dose
da VASPR, mesmo em presença da segunda dose da vacina. Se,
por exemplo, a proporção de imunizados na primeira
dose fosse inferior a 80-85%, a eliminação só
seria possivel se fossem imunizados mais de 60-70% dos indivíduos
ainda susceptíveis na idade da segunda dose. Estes valores
para a segunda dose são provavelmente difíceis de
atingir, atendendo à dificuldade de alcançar os indivíduos
que escaparam à primeira dose (quem “escapou”
à primeira dose tem em geral menos probabilidade de vir à
segunda dose do que quem não escapou à primeira dose).
Uma elevada (> 90-95%) cobertura
vacinal na primeira dose, por outro lado, possibilita a eliminação
das doenças da VASPR com niveis de imunização
moderados ou mesmo baixos (<40%) na segunda dose. A manutenção
de uma forte cobertura vacinal aos 15 meses de idade com a VASPR,
abre portanto perspectivas de eliminação destas doenças
com a segunda dose, não obstante as potenciais dificuldades
em conseguir altas percentagens de comparência nos postos
de vacinação na idade da segunda dose.
|
Regresso
ao topo

|
| |
E quando a vacinação não
elimina a doença ? O
único caso documentado de erradicação de uma
doença infecciosa a nivel planetário é o da
varíola (ver História).
A prática tem demonstrado que, infelizmente, as previsões
pessimistas da teoria matemática acerca da dificuldade de
eliminar doenças transmissíveis, têm-se revelado
correctas. Em Portugal, doenças como o sarampo, difteria,
tosse convulsa, poliomielite etc., baixaram drásticamente
a sua incidência depois da implementação da
vacinação, mas não se podem ainda considerar
eliminadas. A teoria matemática prevê que, quando a
doença não é eliminada pela vacinação,
verifica-se que:
1. A incidência média
da doença baixa drásticamente. Muitos susceptíveis,
potenciais candidatos a apanhar a doença, são imunizados
e directamente retirados do processo de transmissão, tornando
o número de “substitutos” mais baixo, embora
R0 não se altere (ver Dinâmica
de doenças transmissiveis e R0
).
2. A idade média em que a doença
é apanhada (A) torna-se mais elevada. De facto, se há
menos casos de doença a circular, a probabilidade de um indivíduo
susceptível encontrar a doença diminui e, por isso,
o tempo médio que decorre desde ele nascer até encontrar
a doença aumenta. Por exemplo, o sarampo que, antes da vacinação
era em média apanhado em Portugal por volta dos 5-6 anos,
passou a ser apanhado por volta dos 8-10 anos. Esta consequência
da vacinação tem por vezes consequências preversas.
Muitas doenças infantis são relativamente benignas
quando apanhadas muito cedo na vida, mas a probabilidade de originarem
complicações severas aumenta com a idade. Pode-se
assim cair numa situação em que há muito menos
casos de doenças por ano, mas a percentagem de casos com
complicações sérias aumenta.
3. Se a doença exibia epidemias
regulares antes da vacinação, deve continuar a exibi-las.
Porém, o periodo inter-epidémico (T) deve aumentar
depois de se implementar a vacinação. Para compreender
porquê, basta recordar que A entra na equação
que permite calcular o valor de T (ver Epidemias). Como A aumenta
(ponto 2. acima), T também aumenta.
Por exemplo, existe evidência de que antes da vacinação
ocorriam epidemias de sarampo em Portugal aproximadamente de 2 em
2 ou de 3 em 3 anos. Desde a vacinação, as epidemias
têm ocorrido entre nós de 4 em 4 ou de 5 em 5 anos.
|

Página de abertura

Dicionário
Regresso
ao topo |
Regresso
ao topo

Página
de abertura
|
