Conceitos básicos

Objetos e função print()

Essencialmente, um programa em Python consiste num conjunto de comandos a ser executados.

Muitas vezes esses comandos consistem na manipulação de objetos.

Estes objetos estão representados na memória do computador, a cada momento, e têm um determinado valor.

Dois tipos básicos de objetos que podemos criar e manipular num programa são:

• números
• strings

Num programa, podemos apresentar o valor que um objeto tem com a função print().

Um exemplo com números:

print(4)
print(3.2)
print(9.0)
print(((3 + 9) / 3.0)**0.5)

4
3.2
9.0
2.0

Nas expressões podemos usar:

• os cinco operadores + - * / ** (** é a potenciação)
• vários níveis de ()
• o operador %: o resto da divisão (por exemplo, 5 % 3 tem como resultado 2)

Um exemplo com strings:

print('quinta feira')
print('hoje', 'é', "quinta feira,", 16)

quinta feira
hoje é quinta feira, 16

Pequenos textos entre "" ou '' são strings. São sequências de caracteres (os espaços e pontuação, desde que estejam entre as aspas contam como caracteres.

A função print() pode ser usada com vários objetos a apresentar, separados por vírgulas. É inserido um espaço entre os vários objetos. Note-se que, com as strings, as aspas são eliminadas.

Atribuição de nomes a "objetos"

Este é um dos mais fundamentais comandos em programação!

A forma geral é

<nome> = <expressão>

Depois de uma atribuição, o nome pode ser usado em vez do valor do objeto ou expressão. Mesmo em atribuições seguintes, no comando print(), etc.

a = 4
b = 3.2
c = a + b
d = c ** 0.5
print(a)
print(b)
print(c, d)

4
3.2
7.2 2.6832815729997477

hoje = "Hoje é quinta feira"
mês = "Março"
tudo = hoje + ' e estamos em ' + mês

print(hoje)
print(mês)
print(tudo)

Hoje é quinta feira
Março
Hoje é quinta feira e estamos em Março

Que nomes podemos usar?

As regras são:

1. Um nome é uma combinação de letras minúsculas ou maiúsculas (podendo ser acentuadas) ou dígitos (0 to 9) ou o underscore. Nomes como x, Km_1 ou velocidade_da_reaccao são exemplos válidos.
2. Um nome não pode começar com um dígito. 1x é inválido, mas x1 é aceitável.
3. Palavras usadas como comandos da linguagem (keywords) não são permitidas (por exemplo, print).

Não são permitidos espaços ou símbolos como !, @, #, % nos nomes.

tipos de objetos vistos até agora

• inteiros
• floats
• strings

Existem também os complexos (em que j é a unidade imaginária):

c = 4+2j

print('c =', c)

print(c.real)
print(c.imag)

d = 4j

print('c * d =', c * d)

c = (4+2j)
4.0
2.0
c * d = (-8+16j)

Alteração dos objetos associados a um nome

Durante a execução de um programa, os objetos associados a um mesmo nome podem variar:

a = 2
b = 3
c = 'Olá'

b = a + b
a = a + 1
c = a + b

print("a =", a)
print("b =", b)
print("c =", c)

a = 3
b = 5
c = 8

Para melhor compreender as mudanças que ocorrem nos valores atribuídos aos nomes de a, b e c no programa anterior, podemos modifica-lo, mostrando, com print(), os valores atualizados desses nomes, após cada atribuição. Repare-se nos resultados de cada print():

a = 2
b = 3
c = 'Olá'
print("a =", a, "b =", b, "c =", c)

b = a + b
print("a =", a, "b =", b, "c =", c)
a = a + 1
print("a =", a, "b =", b, "c =", c)
c = a + b
print("a =", a, "b =", b, "c =", c)

a = 2 b = 3 c = Olá
a = 2 b = 5 c = Olá
a = 3 b = 5 c = Olá
a = 3 b = 5 c = 8

Interpolação de valores em strings

As strings podem ter valores "interpolados", usando os nomes desses valores ou expressões. Para isso, usam-se {} para identificar em que sítio da string deve ficar cada valor e a string deve ter a letra f como prefixo. Um exemplo:

a = 4.8
b = 3.2
c = a + b

print(f'a é igual a {a}, mas b = {b}, enquanto que c = {c}')

a é igual a 4.8, mas b = 3.2, enquanto que c = 8.0

Comentários

# Comentários começam por #

# Podemos dar nomes a vários objetos
# de uma só vez:
a, b  =  3, "experiência"

print(f"a = {a} b = {b}")

a = 3 b = experiência

a, b  =  3, "experiência"

print(f"a = {a} b = {b}")

# print() deixa uma linha de intervalo
print()

a, b = 3, 4
print(f"a = {a} b = {b}\n")

# Podemos trocar dois nomes desta maneira
a, b = b, a
print('Depois de trocar a e b...')
print(f"a = {a} b = {b}")

a = 3 b = experiência

a = 3 b = 4

Depois de trocar a e b...
a = 4 b = 3

Nota: quando numa string aparece o caractere "especial" \n, este provoca uma linha suplementar quando a string é apresentada com a função print().

Funções disponíveis "integradas" na linguagem (ex. print(), abs() e int())

Além da função print(), as funções int() e abs() fazem parte integrante da linguagem Python.

numero = -3.8
x = int(numero)
y = abs(numero)

print(numero, '\n')
print(x)
print(y)

-3.8 

-3
3.8

Podemos encontrar a lista destas funções na documentação oficial da linguagem Pyhton:

Python Built-in functions

Conversão entre vários tipos de objetos (int(), float(), complex() e str())

As funções int(), float(), complex() e str() fazem conversões para os vários tipos de objetos:

• inteiros
• floats
• complexos (em que j é a unidade imaginária)
• strings

x = 3.8

print(x,'\n')
print(int(x))
print(complex(x))
print(str(x))

3.8 

3
(3.8+0j)
3.8

s = '3.4e4'
f = float(s)
c = complex(s)

print(s, '\n')
print(f)
print(c)

3.4e4 

34000.0
(34000+0j)

As conversões nem sempre são possíveis...

s = 'Vamos ver...'
print(s, '\n')

print(float(s))

Vamos ver... 


---------------------------------------------------------------------------

ValueError                                Traceback (most recent call last)

<ipython-input-15-8e9521c426a4> in <module>()
      2 print(s, '\n')
      3 
----> 4 print(float(s))


ValueError: could not convert string to float: 'Vamos ver...'

Módulos: funções adicionais

Além das funções integradas, existem muitos módulos contendo funções adicionais.

Estes módulos têm de ser importados para que as funções fiquem disponíveis.

Um exemplo é o módulo math que contem muitas funções (e algumas constantes) matemáticas:

import math

x = 2.0

y = math.log(x)
print('ln(2.0) =', y)

y = math.log10(x * 5)
print('ln10(2.0 * 5) =', y)

y = math.exp(x)
print('exp(2.0) =', y)

y = math.sin(x)
print('sin(2.0) =', y)

ln(2.0) = 0.6931471805599453
ln10(2.0 * 5) = 1.0
exp(2.0) = 7.38905609893065
sin(2.0) = 0.9092974268256817

y = math.sin(math.radians(90))
print('sin(90°) =', y)

print('pi =', math.pi)

print('e =', math.e)

y = math.sin(math.pi / 2.0)
print('sin(π / 2) =', y)

sin(90°) = 1.0
pi = 3.141592653589793
e = 2.718281828459045
sin(π / 2) = 1.0

y = math.factorial(100)
print('100! =', y)

100! = 93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000

Um outro exemplo é o módulo calendar que contem muitas funções relacionadas com datas e calendário.

Um exemplo é a função weekday(), que, ao ser dado um ano, mês e dia, calcula um número que representa o dia da semana. (0 - seg, 1 - ter, 2 - qua, 3 - qui, 4 - sex, 5 - sab, 6 - dom)

import calendar

print(calendar.weekday(2017, 3, 30))
#nota: 0:seg 1:ter 2:qua 3:qui 4:sex 5:sab 6:dom

3

Outro exemplo é a função calendar(), que constrói uma string com um calendário de um determinado ano:

import calendar
print(calendar.calendar(2019))

                                  2019

      January                   February                   March
Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su
    1  2  3  4  5  6                   1  2  3                   1  2  3
 7  8  9 10 11 12 13       4  5  6  7  8  9 10       4  5  6  7  8  9 10
14 15 16 17 18 19 20      11 12 13 14 15 16 17      11 12 13 14 15 16 17
21 22 23 24 25 26 27      18 19 20 21 22 23 24      18 19 20 21 22 23 24
28 29 30 31               25 26 27 28               25 26 27 28 29 30 31

       April                      May                       June
Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su
 1  2  3  4  5  6  7             1  2  3  4  5                      1  2
 8  9 10 11 12 13 14       6  7  8  9 10 11 12       3  4  5  6  7  8  9
15 16 17 18 19 20 21      13 14 15 16 17 18 19      10 11 12 13 14 15 16
22 23 24 25 26 27 28      20 21 22 23 24 25 26      17 18 19 20 21 22 23
29 30                     27 28 29 30 31            24 25 26 27 28 29 30

        July                     August                  September
Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su
 1  2  3  4  5  6  7                1  2  3  4                         1
 8  9 10 11 12 13 14       5  6  7  8  9 10 11       2  3  4  5  6  7  8
15 16 17 18 19 20 21      12 13 14 15 16 17 18       9 10 11 12 13 14 15
22 23 24 25 26 27 28      19 20 21 22 23 24 25      16 17 18 19 20 21 22
29 30 31                  26 27 28 29 30 31         23 24 25 26 27 28 29
                                                    30

      October                   November                  December
Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su
    1  2  3  4  5  6                   1  2  3                         1
 7  8  9 10 11 12 13       4  5  6  7  8  9 10       2  3  4  5  6  7  8
14 15 16 17 18 19 20      11 12 13 14 15 16 17       9 10 11 12 13 14 15
21 22 23 24 25 26 27      18 19 20 21 22 23 24      16 17 18 19 20 21 22
28 29 30 31               25 26 27 28 29 30         23 24 25 26 27 28 29
                                                    30 31

Exemplo: raízes da equação do 2º grau

Exemplo:

Calcular as soluções da equação do 2º grau

$a x^2 + b x + c = 0$

ou seja

Dados $a, b$ e $c$, calcular

$x_1 = \frac{-b + \sqrt{b^2 -4 a c}}{2 a}$ e $x_2 = \frac{-b - \sqrt{b^2 -4 a c}}{2 a}$

print('Este programa calcula x tal que a x2 + b x + c = 0')
# testar com os seguintes valores (1,4,1) , (1,2,1) , (1,1,1)

a = 1
b = 4
c = 1

rdelta = (b**2.0 - 4.0 * a * c) ** 0.5

x1 = (- b + rdelta) / (2.0*a)
x2 = (- b - rdelta) / (2.0*a)

print("x1 =", x1)
print("x2 =", x2)

Da matemática, sabemos que uma equação do segundo grau pode ter 2 soluções reais, uma solução real "dupla", ou duas soluções complexas, que neste caso serão complexos conjugados.

Podemos correr o programa várias vezes, para diferentes valores de $a$, $b$, $c$, tentando obter as três situações. Ao fazer isto estamos a testar o programa.

Para fazer estes testes, basta modificar as linhas que definem os valores para a, b e c e voltar a executar o program.

Com a = 1, b = 4, c = 1:

x1 = -0.2679491924311228
x2 = -3.732050807568877

Com a = 1, b = 2, c = 1:

x1 = -1.0
x2 = -1.0

Com a = 1, b = 1, c = 1:

x1 = (-0.49999999999999994+0.8660254037844386j)
x2 = (-0.5-0.8660254037844386j)

O programa funciona e parece dar resultados corretos para as três situações pretendidas (embora se note um pequeno erro no caso das duas soluções complexas que deveria ser, exatamente, dois complexos conjugados).

No entanto, seria mais adequado se o programa pudesse apresentar uma pequena mensagem que indicasse em qual das três situações está o resultado (2 soluções reais ou uma solução real dupla ou duas soluções complexas).

(Podemos também tentar corrigir o pequeno erro).

Para isto, o programa deve ter um comportamento diferente, consoante o tipo de resultado.

Da matemática, sabemos que o que define o tipo de resultado é o valor do "discriminante", $\Delta = b^2 - 4 a c$..

• quando $\Delta > 0$ temos duas soluções reais.
• quando $\Delta = 0$ temos uma solução real (solução dupla).
• quando $\Delta < 0$ temos duas uma soluções complexas (complexos conjugados).

Podemos reescrever o programa de modo a realizar o cálculo das soluções e apresentar uma mensagem de um modo diferente, consoante o valor de $\Delta$ ?

Alternativa if...else

A linguagem Python permite a execução alternativa de blocos de comandos.

Continuando com o exemplo anterior, vamos primeiro distinguir o caso das soluções reais ($\Delta \geqslant 0$) do caso das soluções complexas ($\Delta < 0$).

# Este programa calcula x tal que a x2 + b x + c = 0
# testar com os seguintes valores (1,4,1) , (1,2,1) , (1,1,1)

a, b, c = 1, 1, 1
print('a =', a, 'b =', b,'c =',c, '\n')

# cálculo do discriminante
delta = b**2 - 4.0 * a * c

# separar soluções reais das complexas
if delta < 0.0:
    r_delta = (-delta)**0.5 * 1j
    print('Soluções complexas:')
else:
    r_delta = (delta)**0.5
    print('Soluções reais:')

x1 = (- b + r_delta) / (2.0 * a)
x2 = (- b - r_delta) / (2.0 * a)

print("x1 =", x1, ", x2 =", x2)

Testando agora o programa para as três situações possíveis:

$\Delta > 0$:

a = 1 b = 4 c = 1

Soluções reais:
x1 = -0.2679491924311228 , x2 = -3.732050807568877

$\Delta = 0$:

a = 1 b = 2 c = 1

Soluções reais:
x1 = -1.0 , x2 = -1.0

$\Delta < 0$:

a = 1 b = 1 c = 1

Soluções complexas:
x1 = (-0.5+0.8660254037844386j) , x2 = (-0.5-0.8660254037844386j)

O programa funciona, agora, sem problemas.

É feito um teste ao valor de delta à frente do comando if e é executado um de dois blocos alternativos:

• as linhas entre if e else:, caso delta seja negativo, ou
• as duas linhas depois de else:, caso delta seja positivo.

A forma geral de incluir blocos alternativos com if...else é:

if <condição> :
    <comandos para condição verdadeira>
else:
    <comandos para condição falsa>

Podemos ter várias linhas no bloco if e no bloco else.

É o alinhamento das linhas do programa (também chamada identação) que define define os dois blocos:

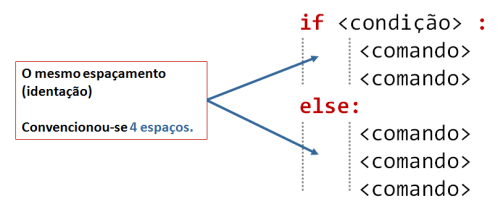
Note-se que, no porgrama anterior, as linhas

x1 = (- b + r_delta) / (2.0 * a)
x2 = (- b - r_delta) / (2.0 * a)

já não pertencem ao bloco else. Isto porque o seu alinhamento é (de novo) igual ao de todas as outras linhas fora dos blocos if...else (e estão alinhadas com as próprias linhas dos comandos if e else)

NOTA: no teste da condição podemos usar:

> (maior)

< (menor)

>= (maior ou igual)

<= (menor ou igual)

== (igual. Nota: são dois sinais de igual consecutivos)

!= (diferente)

O programa está bem melhor na maneira de apresentar os resultados, separando o caso real do complexo.

Mas, perfeito, perfeito, seria tratar o caso em que $\Delta = 0$ de uma forma diferente, tendo o cuidado de apresentar um único valor, no caso de uma raíz dupla.

Precisamos, para isso, que o programa possa se adaptar a cada uma das três alternativas.

Alternativas if...elif...else

Usando o comando elif podemos testar mais do que uma condição e executar em alternativa e, consequentemente, mais do que dois blocos de comandos.

Seguindo o exemplo da resolução de uma equação do segundo grau, podemos separar os três casos associados ao valor de $\Delta$ da seguinte forma:

# Este programa calcula x tal que a x2 + b x + c = 0
# testar com os seguintes valores (1,4,1) , (1,2,1) , (1,1,1)

a, b, c = 1, 4, 1
print('a =', a, 'b =', b,'c =',c, '\n')

# cálculo do discriminante
delta = b**2 - 4.0 * a * c

if delta < 0.0:
    print('Soluções complexas:')
    r_delta = (-delta)**0.5 * 1j
    x1 = (- b + r_delta) / (2.0 * a)
    x2 = (- b - r_delta) / (2.0 * a)    
    print("x1 =", x1, ", x2 =", x2)
elif delta > 0:
    print('Soluções reais:')
    r_delta = (delta)**0.5
    x1 = (- b + r_delta) / (2.0 * a)
    x2 = (- b - r_delta) / (2.0 * a)    
    print("x1 =", x1, ", x2 =", x2)
else:
    print('Solução real (dupla):')
    x = -b / (2.0 * a)
    print("x =", x)

a = 1 b = 4 c = 1 

Soluções reais:
x1 = -0.2679491924311228 , x2 = -3.732050807568877

O comando elif é uma abreviatura de else + if e possibilita o teste de uma nova condição para além daquela já usada no comando if.

Podem ser usados vários comandos elif.

E note-se que, mais uma vez, podemos ter várias linhas em cada bloco : o alinhamento (identação) define os blocos:

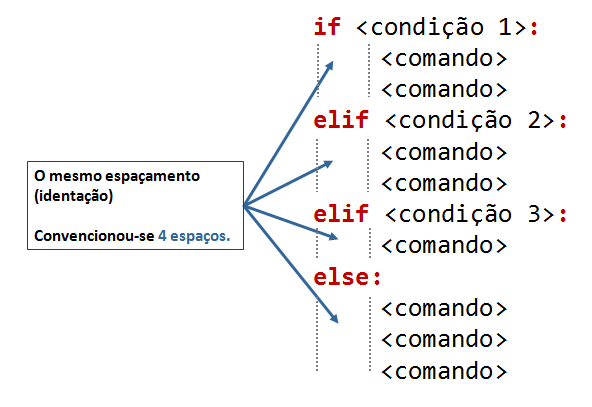
Testando agora o programa para as três situações possíveis:

$\Delta > 0$:

a = 1 b = 4 c = 1

Soluções reais:
x1 = -0.2679491924311228 , x2 = -3.732050807568877

$\Delta = 0$:

a = 1 b = 2 c = 1

Solução real (dupla):
x = -1.0

$\Delta < 0$:

a = 1 b = 1 c = 1

Soluções complexas:
x1 = (-0.5+0.8660254037844386j) , x2 = (-0.5-0.8660254037844386j)

Pode ser usado todo um conjunto de blocos if...else... "dentro" de um bloco if ou elif ou else.

Por exemplo, o o programa também poderia ser escrito da seguinte forma:

# Este programa calcula x tal que a x2 + b x + c = 0
# testar com os seguintes valores (1,4,1) , (1,2,1) , (1,1,1)

a, b, c = 1, 4, 1
print('a =', a, 'b =', b,'c =',c, '\n')

# cálculo do discriminante
delta = b**2 - 4.0 * a * c

if delta == 0.0:
    print('Solução real (dupla):')
    x = -b / (2.0 * a)
    print("x =", x)
else:
    if delta < 0:
        print('Soluções complexas:')
        r_delta = (-delta)**0.5 * 1j
    else:
        print('Soluções reais:')
        r_delta = (delta)**0.5

    x1 = (- b + r_delta) / (2.0 * a)
    x2 = (- b - r_delta) / (2.0 * a)    
    print("x1 =", x1, ", x2 =", x2)

Algumas notas:

NOTA: o bloco else não é obrigatório. Se não fizer sentido a existência de uma condição alternativa ao if, este bloco pode ser omitido.

NOTA: no teste da condição podemos usar:

• Conjunção lógica: and
• Disjunção lógica: or
• Negação: not

Existem também em Python duas "constantes" booleanas:

• Verdade: True
• Falsidade: False

Vejamos agora um outro exemplo da utilização de blocos alternativos.

Exemplo: Regra dos anos bissextos

• Se o ano é divisível por 4, então é bissexto

Regra em vigor até 1582 (calendário Juliano, de Júlio César)

# Este programa determina de um ano é bissexto
# Testar com 2015 N, 2012 S, 1900 N, 2000 S

a = 2015

if a % 4 == 0:
    print(a , "é bissexto")
else: 
    print(a, "não é bissexto")

2015 não é bissexto

Correndo o programa com diferentes valores de a:

2015 nao é bissexto

2012 é bissexto

1900 é bissexto

2000 é bissexto

Este programa parece falhar para 1900. Isto acontece porque, na realidade, a regra actual dos anos bissextos é um pouco mais complexa.

Exemplo: Regra dos anos bissextos (calendário moderno)

• Se o ano é divisível por 4, então é bissexto
• Excepto os que são divisíveis por 100: não são bissextos
• Excepto os divisíveis por 100 que sejam exactamente divisíveis por 400: são bissextos.

Esta regra entrou em vigor após 1582 (calendário Gregoriano, do papa Gregorio XIII)

Da aplicação desta regra resulta que alguns anos de mudança de século (sempre divisíveis por 4) não sejam bissextos. É o caso de 1900. E alguns anos de mudança de século, por exemplo os anos 1600; 2000; 2400, sejam bissextos.

Podemos adaptar o programa anterior para incluir as duas últimas regras:

a = 2015

if a % 4 == 0 and not (a % 100 == 0 and not a % 400 == 0):
    print(a , "é bissexto")
else: 
    print(a, "não é bissexto")

2015 não é bissexto

Correndo o programa com diferentes valores:

2015 nao é bissexto

2012 é bissexto

1900 nao é bissexto

Reparar que o resultado é diferente para 1900.

2000 é bissexto

Os interessados na história da introdução do calendário gregoriano podem consultar o artigo

http://en.wikipedia.org/wiki/Gregorian_calendar

É desaconselhável escrever uma condição tão complicada num comando if: prejudica muito a legibilidade do programa.

Um programa equivalente, combinando vários blocos de if...else... e a negação lógica not que será (possivelmente) mais fácil de perceber é:

a = 2015

if not a % 4 == 0:
    print(a, "não é bissexto")
else:
    if not a % 100 == 0:
        print(a , "é bissexto")
    else:
        if a % 400 == 0:
            print(a , "é bissexto")
        else:
            print(a , "não é bissexto")

2015 não é bissexto

Correndo o programa com diferentes valores de a:

2015 não é bissexto
2012 é bissexto
1900 não é bissexto
2000 é bissexto

Função input()

Até agora, nos exemplos foram apresentados, são incluídos no programa os valores a partir dos quais se fazem os cálculos (tradicionalmente chamados o input do programa).

Por exemplo, nos exemplos da resolução de uma equação do segundo grau incluímos no princípio do programa os valores dos coeficientes:

a, b, c = 1, 4, 1

Os programas partem destes valores, realizam cálculos e apresentam resultados.

A linguagem Python suporta também um outro mecanismo: o pedido de valores ao utilizador durante a execução do programa.

A função input() tem este papel: duarnte a execução de um programa, ao passar por uma função input() o programa pára esperando que seja introduzido uma string. A função permite também seja apresentada uma mensagem de indicação do que está a ser pedido.

Vejamos com um exemplo:

a = input('Valor de a? ')
b = input('Valor de b? ')
c = input('Valor de c? ')

a = float(a)
b = float(b)
c = float(c)

# cálculo do discriminante
delta = b**2 - 4.0 * a * c

if delta == 0.0:
    print('Solução real (dupla):')
    x = -b / (2.0 * a)
    print("x =", x)
else:
    if delta < 0:
        print('Soluções complexas:')
        r_delta = (-delta)**0.5 * 1j
    else:
        print('Soluções reais:')
        r_delta = (delta)**0.5

    x1 = (- b + r_delta) / (2.0 * a)
    x2 = (- b - r_delta) / (2.0 * a)    
    print("x1 =", x1, ", x2 =", x2)

Valor de a? 1
Valor de b? 1
Valor de c? 1
Soluções complexas:
x1 = (-0.5+0.8660254037844386j) , x2 = (-0.5-0.8660254037844386j)

Executando este programa várias vezes, testeando com os diferentes casos, agora os valores dos coeficientes são "pedidos" pelo programa:

Valor de a? 1
Valor de b? 4
Valor de c? 1
Soluções reais:
x1 = -0.2679491924311228 , x2 = -3.732050807568877

Valor de a? 1
Valor de b? 2
Valor de c? 1
Solução real (dupla):
x = -1.0

Valor de a? 1
Valor de b? 1
Valor de c? 1
Soluções complexas:
x1 = (-0.5+0.8660254037844386j) , x2 = (-0.5-0.8660254037844386j)