Os algarismos da civilização chinesa

    A civilização chinesa tem uma longa história. A sua principal característica foi, até o século XIX, a imutabilidade de determinados elementos da sua cultura milenar como o cultivo de cereais, a escrita, a importância da família ou o culto aos antepassados. Enquanto sociedade tradicional, os chineses pensavam que a melhor forma de viver não consistia em modernizar-se mas em repetir arquétipos do passado.
    A civilização chinesa desenvolveu-se ao longo das margens do rio Amarelo e do Azul, desde o 3º milénio a.C. durante  a dinastia Hsia iniciada pelo imperador Yu. Continuou com a dinastia Shang que, por volta de 1500 a.C.,  ocupou a região de Shangai. Desta dinastia provêm os primeiros numerais chineses inscritos sobre carapaças de tartarugas e ossos de animais.  
    O grande império desintegra-se, por volta do 700 a.C.. Aproximadamente até 400 a.C., a China é um conjunto de estados independentes em permanente guerra uns com os outros.  É desta altura o primeiro texto sobre matemática - o Chou Pei Suan Ching.  Para além de uma breve explicação sobre o cálculo aritmético, este texto contém um diálogo sobre as propriedades dos triângulos rectângulos, no qual o teorema de Pitágoras é enunciado  e dada uma sua demonstração geométrica.
   

Os algarismos chineses

    O sistema de numeração chinês é baseado num sistema gráfico com muitas formas abstractas e combinações de sinais arcaicos.

    Um traço horizontal simbolizava a unidade, dois traços duas unidades e, analogamente, para três e quatro. A incapacidade de identificar directamente uma série de mais de quatro sinais idênticos não permite que este processo se repita continuamente. Sendo assim, para representar o algarismo 5, utilizavam traços que formavam um X fechado em cima e em baixo. O algarismo 6 era simbolizado por um V invertido ou ainda por um desenho em forma de templo. Para o algarismo 7 era utilizada uma cruz e duas semicircunferências de "costas" uma para a outra eram o símbolo utilizado para o algarismo 8. Para o 9 era usado um símbolo que faz lembrar o anzol.

    Pensa-se que a escolha dos símbolos usados na representação dos algarismos chineses, ficou a dever-se à semelhança fonética que existia entre o símbolo e a palavra oral correspondente aos algarismos. Este facto poderia explicar a escolha de um homem para representar o 1 000.

    Mas esta não é a única explicação: a escolha dos símbolos pode também ter sido de ordem religiosa.

					ou ou	ou	ou	ou		ou	ou
1	2	3	4	5	6	7	8	9	10	100	1 000

    Neste sistema, as dezenas, centenas e milhares são representadas segundo o principio multiplicativo, ou seja, agrupando os sinais correspondentes aos números necessários para obter o produto pretendido. Todos os outros números podem ser obtidos através de uma composição dos princípios multiplicativo e aditivo, tal como ilustra a figura seguinte:

    Assim, o número 656 é representado da seguinte forma:

    Mais tarde, este sistema sofreu algumas transformações, obtendo-se o seguinte sistema:

1		10
2		100
3		1 000
4		10 000
5
6
7
8
9

    Com base neste novo sistema, a notação dos múltiplos consecutivos de cada uma das quatro potências de dez fica:

Dezenas		Centenas		Milhares		Dezenas de milhar
10	1×10	100	1×100	1 000	1×1 000	10 000	1×10 000
20	2×10	200	2×100	2 000	2×1 000	20 000	2×10 000
30	3×10	300	3×100	3 000	3×1 000	30 000	3×10 000
40	4×10	400	4×100	4 000	4×1 000	40 000	4×10 000
50	5×10	500	5×100	5 000	5×1 000	50 000	5×10 000
60	6×10	600	6×100	6 000	6×1 000	60 000	6×10 000
70	7×10	700	7×100	7 000	7×1 000	70 000	7×10 000
80	8×10	800	8×100	8 000	8×1 000	80 000	8×10 000
90	9×10	900	9×100	9 000	9×1 000	90 000	9×10 000

    Para representar números muito grandes, os chineses tomavam a dezena de milhar como unidade de contagem. Então, a representação de potências consecutivas de 10 era:

104			1×104	108			1×104×104
105			10×104	109			10×104×104
106			1×102×104	1010			1×102×104×104
107			1×103×104	1011			1×103×104×104

    Consideremos assim o número 487 390 629 = (4×10⁴+8×10³+7×10²+3×10+9)×10⁴+(6×10²+2×10+9), cuja representação é a seguinte:

(4	×	104	+	8	×	103	+	7	×	102	+	3	×	10	+	9)	×	104	+	(6	×	102	+	2	×	10	+	9)

Sistema posicional

    O sistema posicional utilizado pelos chineses é quase idêntico à numeração moderna. Consiste numa representação dos números na qual o valor de cada algarismo dependia do lugar onde este se encontrava na leitura dos números. Neste utilizava-se um sistema de representação dos nove algarismos que resultava da combinação de barras horizontais e verticais, tal como ilustra a figura:   

1	2	3	4	5	6	7	8	9

 Para representar o número 12 tínhamos então:

12

Para evitar os equívocos que esta representação poderia suscitar (por exemplo a representação do 12 poderia ser confundida com a do 3, ou com a do 21), a notação foi reformulada do modo seguinte:   

1	2	3	4	5	6	7	8	9

    Mais tarde, para distinguir as ordens das unidades, decidiu-se representar as ordens de grandeza intercaladamente, com barras verticais e horizontais. As unidades simples, as centenas, as dezenas de milhar, etc, eram representadas através de barras verticais, as dezenas, os milhares, as centenas de milhar, etc. eram representadas por barras horizontais. Para tal elucidar, considere-se a representação do número 174:

1	7	4

    No entanto, continuaram a surgir equívocos, principalmente nos casos em que o zero, desconhecido na altura, intervinha na representação do número, como por exemplo:

7	6	4		7	0	6	4		7	0	6	4	0

 Este problema foi ultrapassado de várias maneiras:

• Introduzindo, no lugar do zero, os símbolos das potências de dez utilizados na numeração tradicional:

7	6	4	"cem"
76 400

• Recorrendo ao sistema de representação tradicional:

	7
	×
	10 000
	+
	6
	×
	1 000
	+
	4
	×
	100
	76 400

• Introduzindo os algarismos em quadrados, deixando vazio aquele que correspondia ao zero:

   

  7	6	4	0	0
  76 400

   

• Introduzindo um círculo para designar o zero:

7	6	4	0	0
76 400

Como calculavam os chineses

Tabuleiro de bastonetes

    Para realizar operações, os chineses utilizavam pequenos bastonetes aos quais chamavam chóu (fichas de cálculo) que organizavam numa mesa ladrilhada. Nesta, cada coluna correspondia a uma determinada ordem decimal: a da esquerda correspondia às unidades, a seguinte às dezenas, a outra às centenas e assim sucessivamente. Para se representar um número colocavam-se, nas colunas e segundo uma linha previamente escolhida, tantos palitos quantos os correspondentes à ordem decimal. Como exemplo, tomemos a representação de alguns números no tabuleiro chinês:

dezenas de milhar	milhares	centenas	dezenas	unidades
						60 031
						52 759

    As adições e subtracções implicavam a representação dos números no tabuleiro chinês e, posteriormente, a reunião  ou subtracção desses mesmos números, coluna a coluna.

    Para a multiplicação, o método era igualmente simples: o multiplicador era representado no topo do tabuleiro e o número a multiplicar mais a baixo. Os produtos parciais eram colocados nas linhas que ficavam entre os dois números e eram somados à medida que iam aparecendo.

		3	2	9						2	9
					multiplicador
												5º resultado parcial (47 300+1 000)
					multiplicando
1	5	1					1	5	1
		3	2	9						2	9
					1º resultado parcial (30 000)							6º resultado parcial (48 300+20)
1	5	1					1	5	1
		3	2	9							9
					2º resultado parcial (30 000+15 000)							7º resultado parcial (48 320+900)
1	5	1					1	5	1
		3	2	9							9
					3º resultado parcial (45 000+300)							8º resultado parcial (49 220+450)
1	5	1					1	5	1
			2	9							9
					4º resultado parcial (45 300+2 000)							9º resultado parcial (49 670+9)
1	5	1					1	5	1

    Na divisão, o divisor era colocado na linha de baixo, o dividendo na do meio e o quociente na de cima. Este último obtinha-se retirando do dividendo os resultados dos produtos parciais.

Ábaco de contas

    O ábaco de contas chinês, o suan pan (prancheta de cálculo), era um rectângulo de madeira dividido em duas partes e composto por vários arames sobre os quais estão enfiadas sete contas móveis, cinco na parte de baixo e duas na de cima. Cada parte continha várias hastes que correspondiam a uma determinada ordem decimal (da direita para a esquerda: centésimas, décimas, unidades simples, dezenas, centenas, etc). Cada uma das fichas da parte inferior valia uma unidade e cada uma das da parte superior valia cinco unidades quando deslocadas para baixo.

 Representação do número 234 no ábaco de contas chinês .

    Este ábaco permitia efectuar qualquer operação de forma simples e rápida.

    Para adicionar bastava ter em conta o princípio aditivo.

    Consideremos a soma dos números 234, 432 e 567.

    A subtracção é feita procedendo no sentido inverso.

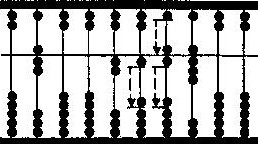
    Para a multiplicação, efectuam-se os produtos parciais que vão sendo somados. O resultado obtido é o produto pretendido.

    Tomemos a multiplicação de 7 por 24:

 

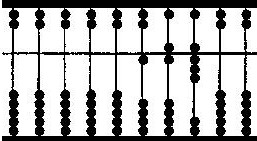    A divisão consistia em subtrair-se o divisor do dividendo o maior número de vezes possível, sendo o resultado encontrado o quociente pretendido.