 Os algarismos da civilização romana
Os algarismos da civilização romana
 Os algarismos da civilização romana
Os algarismos da civilização romana
Grande parte da organização do mundo moderno deve-se ao império que Roma foi capaz de construir há mais dois mil anos nas margens do mar Mediterrâneo. Os idiomas falados no sul da Europa, América Latina, algumas zonas de África e outras partes do mundo constituem uma das heranças directas desta civilização.
Embora os romanos sejam
autores de muitas construções impressionantes, mostraram pouco interesse pela
matemática pura. Os matemáticos romanos dedicaram-se a assuntos práticos, como
comércio e ciências militares. No entanto, foram autores de um sofisticado
sistema de numeração.
Os algarismos romanos
Os algarismos romanos derivam essencialmente da prática do entalhe num osso ou num bastão de madeira. Assim sendo, o algarismo um era simbolizado por um entalhe vertical, pois era o que mais se aproximava da representação manual utilizada pelo homem. Esta explicação também é válida para os algarismos dois, três e quatro.
A dificuldade de identificar directamente uma série de mais de quatro sinais idênticos não permite que este processo se repita continuamente. Sendo assim, para representar o algarismo 5 foi escolhido um entalhe oblíquo, sugerido pela inclinação do polegar em relação aos outros dedos, essa representação sofreu posteriormente alterações chegando até nós como V.
|
|
Várias representações do algarismo 5.
A representação através de entalhes verticais continuou a ser utilizada até ao algarismo nove. Para o algarismo 10, que correspondia ao número de dedos das duas mãos, a representação escolhida foi o cruzamento de dois entalhes oblíquos com diferentes direcções, sugerido pela posição dos dois polegares.
Várias representações do algarismo 10.
Este processo repete-se continuamente até surgir a necessidade de se inventar um outro símbolo, o que acontece quando se atinge o número 50. Assim sendo, para o representar decidiu-se acrescentar um traço à representação do algarismo 5.
Várias representações do algarismo 50.
Para a centena sentiu-se novamente a necessidade de introduzir outra notação, que consistiu em acrescentar um ou dois traços à representação do algarismo 10, ou então considerando o duplo de uma das representações do algarismo 50.
Várias representações do algarismo 100.
Com efeito, o sistema de numeração que deu origem ao sistema romano hoje conhecido, tinha a seguinte forma:
|
|
|
|
|
|
|
|
| 1 | 5 | 10 | 50 | 100 | 500 | 1 000 |
Ao longo do tempo, este sistema foi sujeito a diversas transformações gráficas até originar o sistema romano que chegou até nós.
| 1 |
|
® | I | |||||||||||
| 5 |
|
® | V | |||||||||||
| 10 |
|
® | X | |||||||||||
| 50 |
|
® |
|
® |
|
® |
|
® |
|
® | L | |||
| 100 |
|
® |
|
® | C | |||||||||
| 500 |
|
® |
|
® |
|
® |
|
® | D | |||||
| 1 000 |
|
® |
|
® |
|
® |
|
® |
|
® |
|
® |
|
®M |
Evolução gráfica do sistema romano.
Inicialmente a numeração romana foi baseada no princípio da adição, como mostra o exemplo:
MMMDCCCCXXXXVIIII = 3 949
Numa fase posterior, de forma a simplificar a notação, foi introduzida uma notação seguindo o princípio subtractivo. Assim sendo, a representação do número anterior passou a ser: MMMCMXLIX.
Para números maiores, os romanos adoptaram duas representações gráficas possíveis:
|
5 000 |
ככו |
V |
(5×1 000) |
|
10 000 |
ccככו |
X |
(10×1 000) |
|
50 000 |
כככו |
L |
(50×1 000) |
|
100 000 |
cccכככו |
C |
(100×1 000) |
Como calculavam os Romanos
A palavra ábaco (abacus em latim) deriva da palavra grega abax que significa travessa ou mesa. Do ábaco fazem parte dispositivos que podiam servir para jogos ou para cálculo aritmético. Estas peças de contagem foram chamadas de pséphoi pelos gregos (que significa pedra, número) ou calculus, pelos romanos.
O ábaco de fichas
Para representar um número neste ábaco, as fichas eram dispostas por colunas segundo as unidades, dezenas, centenas, etc., que esse número tinha (quando se atingiam as dez fichas numa coluna estas eram substituídas por uma ficha na coluna de grandeza imediatamente superior).
Posteriormente, com vista a simplificar a representação, acrescentou-se uma linha sobre as ordens de grandeza onde cada ficha colocada vale metade da grandeza imediatamente superior. Na linha inferior, cada ficha vale uma unidade da ordem correspondente.
Para clarificar as explicações anteriores, considerem-se as seguintes representações do número 4 537.
| C | X | M | C | X | I | · | · | ||||||||
|
· · · · |
· · · · · |
· · · |
· · · · · · · |
C | X | M | C | X | I | ||||||
|
· · · ·
|
· · · |
· · |
|||||||||||||
| 4 | 5 | 3 | 7 | 4 | 5 | 3 | 7 |
Princípio do ábaco de fichas Simplificação do ábaco de fichas
Para adicionar representavam-se os dois números no mesmo ábaco procedendo depois à organização das fichas como nos casos anteriores para proceder à sua leitura. As subtracções eram realizadas de forma análoga.
A multiplicação consiste em fazer os diferentes produtos parciais, representando-os de forma acumulada no ábaco. Depois de representados todos os produtos procede-se à organização das fichas obtendo-se o resultado que se pretendia.
Consideremos então a seguinte multiplicação: 630×42
| 2 | 4 | 1 | 2 | 1 | 2 | 6 | ||||||||||||||||||||||||||||
| C | X | M | C | X | I | C | X | M | C | X | I | C | X | M | C | X | I | C | X | M | C | X | I | |||||||||||
| 1º produto parcial (6×4) |
○ ○ |
○ ○ ○ ○ |
2º produto parcial (6×2) |
· · |
· · · · ○ |
○ ○ |
3º produto parcial (3×4) |
· · |
· · · · · ○ |
· · ○ ○ |
4º produto parcial (2×3) |
· · |
· · · · · · |
· · · · |
○ ○ ○ ○ ○ ○
|
|||||||||||||||||||
|
Multiplicador 42
|
Multiplicador 42
|
Multiplicador 42
|
Multiplicador 42
|
|||||||||||||||||||||||||||||||
|
· · · ·
|
· · |
· · · ·
|
· · |
· · · ·
|
· · |
· · · ·
|
· · |
|||||||||||||||||||||||||||
| · |
Multiplicando 630 |
· |
Multiplicando 630
|
Multiplicando reduzido 30
|
Multiplicando reduzido 30
|
|||||||||||||||||||||||||||||
| · |
· · · |
· |
· · · |
· · · |
· · · |
Obtemos assim o seguinte resultado:
| · | · | ||||
| C | X | M | C | X | I |
|
· · |
· |
· · · · |
· | ||
| 2 | 6 | 4 | 6 | 0 |
Ábaco de cera
A representação no ábaco de cera é idêntica à do ábaco de fichas, no entanto, em vez destas, utilizavam-se os números romanos. Com efeito, consideremos o seguinte exemplo: 630×42
| C |
X |
I |
C |
X |
I |
|
|
|
C |
X |
I |
C |
X |
I |
|
|
|
C |
X |
I |
C |
X |
I |
|
|
|
C |
X |
I |
C |
X |
I |
|
|
|
C |
X |
I |
C |
X |
I |
|
|
|
|
|
|
|
|
|
|
|
II |
IV |
|
|
|
|
|
|
|
II |
IV |
|
|
|
|
|
|
|
II |
IV |
|
|
|
|
|
|
|
II |
IV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
II |
|
|
|
|
|
|
|
I |
II |
|
|
|
|
|
|
|
I |
II |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
II |
|
|
|
|
|
|
|
I |
II |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VI |
|
|
|
|
|
|
IV |
II |
|
|
|
|
|
|
|
IV |
II |
|
|
|
|
|
|
|
IV |
II |
|
|
|
|
|
|
|
IV |
II |
|
|
|
|
|
|
|
IV |
II |
|
|
|
|
VI |
III |
|
|
|
|
|
|
|
VI |
III |
|
|
|
|
|
|
|
VI |
III |
|
|
|
|
|
|
|
VI |
III |
|
|
|
|
|
|
|
VI |
III |
|
O resultado obtido é:
| C | X |
I |
C |
X |
I |
|
|
II |
VI |
IV |
VI |
|
|
|
2 |
6 |
4 |
6 |
0 |
Ábaco romano de "bolso"
Este ábaco era constituído por uma série de ranhuras verticais que representavam uma determinada ordem de grandeza: 8 em cima e 9 em baixo. Cada uma das filas de cima tinha uma única peça, enquanto que, nas filas de baixo, existiam 4 peças. Para representar um número na fila de baixo, bastava deslocar as peças para cima e, quando fossem necessárias 5 peças, deslocava-se a peça da fila de cima para baixo.
Consideremos o exemplo da representação do número 52 842:
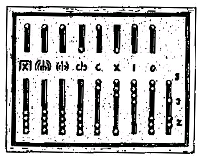 |
Nota: as duas ranhuras à direita serviam para marcas as divisões do as (fracções da unidade monetária usadas no comércio pelos romanos).
| Página inicial | Civilização Suméria | Civilização Egípcia | Civilização Romana | Civilização Chinesa | Civilização Indiana | Civilização Árabe | Quem Somos |