Ciclóide

Conta-se que, numa noite em que sofria de uma dor de dentes, Pascal começou a pensar na ciclóide e quando se apercebeu já a dor de dentes tinha desaparecido. Ele tomou isto como um sinal de Deus, e estudou a ciclóide mais profundamente.

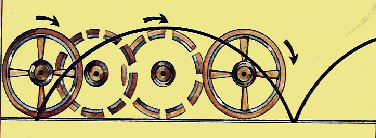
A ciclóide é um arco formado a partir de um ponto numa circunferência, quando esta rola ao longo de uma superfície. Devido às suas propriedades foi a curva mais estudada durante dezassete séculos.

Pascal descobriu certas áreas, volumes e centros de gravidade associados à ciclóide.

Algumas das suas propriedades descobertas no séc. XVII são:

• o seu comprimento é 4 vezes o diâmetro da circunferência que a gera;

• a área limitada pelo arco é o triplo da área do círculo que roda;

• o ponto da circunferência que descreve a ciclóide assume diferentes velocidades;

• ... 

Duas características interessantes desta curva são:

• Se um objecto desliza sobre a curva, livre de atrito e sujeito à aceleração da gravidade, o tempo que demora para alcançar o ponto mais baixo da curva é sempre o mesmo. Independente do ponto de partida do objecto. Por este motivo também se dá o nome de Tautócrona (tempos iguais).

• Se várias curva se unirem num determinado ponto com o ponto mais baixo da curva entre elas, a curva na qual o objecto demora menos tempo para vir do ponto de intersecção ao ponto mais baixo é a ciclóide. Evido a isto também se chama Braquistócrona (menor tempo).

CURIOSIDADE:

Conta a história que Pascal colocou algumas questões sobre a ciclóide, oferecendo um prémio a quem solucionasse as questões, como era habitual na época.

Como as poucas soluções apresentadas continham, pelo menos, alguns erros de cálculo o prémio não foi oferecido, tendo posteriormente Pascal publicado as suas próprias soluções. Tal despertou os ânimos da comunidade matemática pois alguns achavam que tinham direito ao prémio, outros porque Pascal nas suas resoluções só mencionava Roberval, não fazendo referencia a Torricelli, que havia estudado, também a ciclóide.