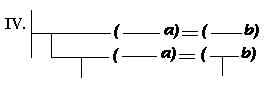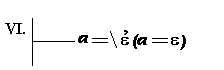Depois da obra de Leibniz e Boole (1815-1864), o grande passo em frente em lógica é dado por Frege (1848-1925). Enquanto que Boole queria mostrar que a lógica era uma parte da matemática, Frege pretendeu mostrar que a aritmética era idêntica à lógica. A sua tese não poderia ser estabelecida satisfatoriamente enquanto não fossem introduzidos em lógica dois importantes melhoramentos . "Em primeiro lugar, o material tradicional e as novas contribuições de Leibniz eBoole tinham que ser organizados de maneira a tornar clara a estrutura da ciência e a grande variedade de formas proposicionais a serem consideradas na lógica geral. Em segundo lugar, tudo o que era exigido para a demonstração dos termos tinha que figurar explicitamente no ínicio e o processo de dedução teve que ser reduzido a um pequeno número de regras padrão a fim de que não houvesse perigo de, inconscientemente, introduzirmos nas demonstrações aquilo que precisamente desejavamos demonstrar. Foi para fazer face a estas duas exigências de sistema e rigor formal que Frege em 1879 apresentou o seu Begriffschrift."1 Como o seu nome sugere, esta obra é um manual de ideografia ou escritura conceptual.
O principal objectivo desta obra é a construção de uma linguagem formalizada do pensamento puro, isto é, um sistema de notação mais regular do que a linguagem do quotidiano e melhor adaptado para garantir a exactidão na dedução. No subtítulo, Frege diz que o modelo para a sua obra é fornecido pela linguagem da aritmética, mas rapidamente se vê que a semelhança principal consiste no emprego de letras para exprimir a generalidade. É claro que Frege não foi o primeiro lógico a pensar neste artificio, porque já Aristóteles (384-322 A.C.) o tinha usado muito antes da intervenção da álgebra. Símbolos aritméticos como "+" não foram usados por Frege em nenhum sentido lógico especial, uma vez que ele pretendia conservá-los no seu uso normal em matemática, embora em conjunção com os seus novos símbolos lógicos.
Alguns exemplos dos símbolos lógicos de Frege:
Símbolo |
Sua designação |
|
Destina-se a exprimir o conteúdo do juízo; |
|
Traço-conteúdo – serve para mostrar que o conteúdo expresso pelo símbolo está sob consideração sem que o autor o afirme ou negue; |
|
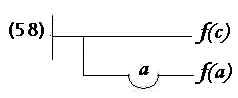
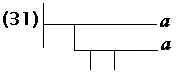
Condição. Exemplo:
|
|
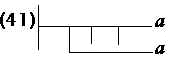
Negação. Exemplo: |
|
Identidade de conteúdo. Exemplo:
|
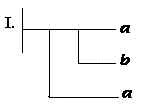
Terminologia de Frege de funções e argumentos:
| Símbolo | Sua designação |
| Exprime uma função indeterminada cujo argumento é G ; | |
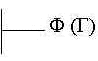 |
G tem a propriedade F ; |
| É uma função de dois argumentos, G e D tomados por esta ordem; | |
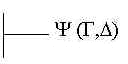 |
G está na relação Y com D ; |
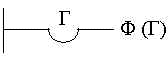 |
Quantificador universal. Este símbolo significa que a função é um facto seja qual for a interpretação que dermos ao argumento. "Tudo é F "; |
Note-se que não há limite para a complexidade das afirmações que podem ser expressas na notação de Frege. Embora só tenha três símbolos básicos relevantes, os símbolos de condição, negação e o quantificador universal, estes podem no entanto ser combinados em infinitas maneiras diferentes. Frege ofereceu, assim, um esquema que é, ao mesmo tempo, mais simples do que qualquer esquema anterior e, num certo sentido, inesgotável.
Nesta mesma obra, além de ter explicado a sua notação, Frege também estabelece algumas teses lógicas, e princípios lógicos tais como:
 |
 |
 |
 |
 |
 |
 |
 |
|
Os primeiros três tratam do conceito expresso pelo traço de condição e os três seguintes introduzem a noção de negação. Dois tratam da identidade de conteúdo e um trata da universalidade (Frege nunca explicou claramente porque é que a lógica devia de ter axiomas).
Na parte final desta obra, a intenção de Frege foi a de mostrar de uma maneira preliminar como a sua notação poderia ser usada para a formulação exacta de noções exigidas pela matemática e escolhe para seu exemplo a teoria geral das sucessões.
Contudo, a Begriffschrift não teve grande acolhimento por parte dos matemáticos e dos filósofos. Frege chegou mesmo a observar que não havia qualquer esperança de compreensão, quer por parte dos matemáticos, quer por parte dos filósofos.

Em 1884, Frege apresentou um novo livro Die Grundlagen der Arithmetik. Nesta
obra, Frege expôe informalmente as suas opiniões e críticas a teorias opotas acerca da
natureza da aritmética e apresenta depois a sua própria teoria. Nela qual analisa os
conceitos básicos da matemática de tal maneira que a redução da aritmética a
operações de carácter essencialmente lógico se torna verosímil. Digamos que, embora
tivesse sido desencorajado pela recepção do seu Begriffschrift, Frege ainda matinha esperanças de publicar uma
demonstração rigorosa da identidade entre a aritmética e a lógica.

Pelo fim da década, Frege
voltou a esta tarefa. Em 1893 apareceu o primeiro volume da sua obra fundamental Die
Grundgesetze der Arithmetik, na qual formaliza a teoria dos Grundlagen, uma tarefa cuja realização
tornou necessário formular a primeira teoria formal das classes; foi esta teoria que foi
depois exibida como inconsistente através do paradoxo de Russell.. Nesta mesma obra
Frege reinterpretou símbolos que tinha introduzido no Begriffschrift, conservando-os
excepto o da identidade
|
que substituiu pelo sinal vulgar de igualdade
|
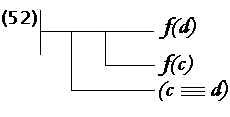
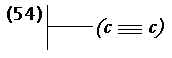
Também estabeleceu os seguintes axiomas ou leis básicas:
|
 |
|
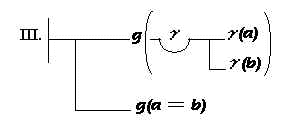 |
|
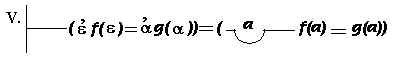 |
|
Enquanto trabalhava no Grundgesetze, Frege modificou algumas das suas concepções anteriores sobre a filosofia da lógica.
Contudo, mais uma vez a recepção da obra foi de novo desencorajante e Frege não publicou o segundo volume dos Grundgesetze senão em 1903. Este trata particularmente da teoria dos números reais. Um imenso espaço é ocupado a criticar opiniões correntes e, no fim, Frege admite que há imenso que fazer antes de se poderem definir correctamente os números reais. Num apêndice escrito depois da maior parte da obra ter sido impressa, Frege confessa a ruína da mesma, motivada pela descoberta implícita, nas premissas dos Grundgesetze, nomeadamente o Axioma (V) 2, que foi exibido através do paradoxo de Russell. A reacção do próprio Frege ao paradoxo , após um inicial período de compreensível consternação foi a de experimentar algumas técnicas que poderiam eliminar a contradição. Porém, veio a verificar-se que o resultado não era aceitável e foi apenas com o estudo de Zermelo que se conseguiu uma formulação satisfatória.
1 - Extraído de: Kneale, W., Kneale, M. (1980). O Desenvolvimento da Lógica. Lisboa: 2ª ed. p.452
2 - Axioma (V) Lê-se da seguinte forma: Se dois conceitos f(x) e g(x) têm sempre o mesmo valor para o mesmo argumento então as suas extensões são as idênticas.
|
|
Para a carta de Russell para Frege
|
| Para a carta de Frege para Russell |
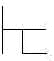
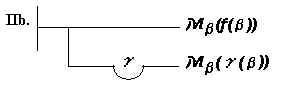
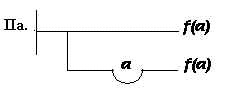
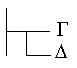 . – Exprime
o juízo de que G não deve ser negado enquanto D é afirmado.
. – Exprime
o juízo de que G não deve ser negado enquanto D é afirmado.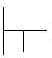
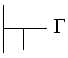 –
Não é verdade que G .
–
Não é verdade que G .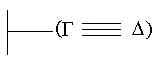 – O nome G e o nome D têm o mesmo conteúdo
conceptual, de tal maneira que G pode ser sempre substituído
por D e reciprocamente;
– O nome G e o nome D têm o mesmo conteúdo
conceptual, de tal maneira que G pode ser sempre substituído
por D e reciprocamente;